局部敏感哈希LSH(Locality Sensitive Hashing)

LSH(Locality Sensitive Hashing)

• 一、局部敏感哈希LSH
• 二、Hamming 距离
• 三、Euclidean 距离
• 四、Jaccard 系数
• 五、参考资料

在很多问题中，从海量数据库中寻找到与查询数据相似的数据是一个很关键的问题。比如在图片检索领域，需要找到与查询图像相似的图片，又比如在3D维重建和 视觉SLAM等问题中，需要在3维点云模型（数据库）中找到与查询描述子最相近的描述子，以实现特征匹配。这个问题也叫近似近邻问题 Approximate Near Neighbor。当数据中的数据量很大时（百万以上），线性查找是不实际的，kd-tree是一个很好算法，但是当数据的维数很高时，kd-tree的性能将变得很差（kd-tree只适用数据在30维以下）。对于高维数据的海量数据近邻查找，局部敏感哈希是一个很好的解决方法。

局部敏感哈希（Locality Sensitive Hashing）是一个方法，应用到不同数据的距离度量时，两个数据之间的相似性（相似性往往是和距离是负相关的）有不同的衡量，那么就需要不同的算法。下面我先总体介绍局部敏感哈希方法，然后针对不同的距离度量空间来具体展开介绍，主要包括了Hamming距离、Euclidean距离、Jaccard 系数、余弦相似度。

如上图是一个图片检索的例子，应用LSH可以从海量数据库中快速检索出所查询的图片。

---

一、局部敏感哈希LSH

先说说哈希Hash，哈希是通过一个哈希函数（Hash function）将数据映射到一个哈希表（Hash Table），通过哈希表的索引，来使搜索时间从线性搜索的O(N)降到O(1)。这里的关键在于哈希函数的选取，对于不同的应用和数据会有不用的哈希函数。

局部敏感哈希的基本思想：在高维数据空间中的两个相邻的数据被映射到低维数据空间中后，将会有很大的概率任然相邻；而原本不相邻的两个数据，在低维空间中也将有很大的概率不相邻。通过这样一映射，我们可以在低维数据空间来寻找相邻的数据点，避免在高维数据空间中寻找，因为在高维空间中会很耗时。有这样性质的哈希映射称为是局部敏感的。

局部敏感哈希定义：

一个哈希函数族满足如下条件时，被称为是 (R,cR,P1,P2) -sensitvie，对于任意两个点  p，q∈Rd ：

为了让局部敏感哈希函数族起作用，需要满足 c>1 ， P1>P2 .

举个例子来说明这个概念。考虑二进制的两个数据点 p,q ，它们的每一个比特位要么是0要么是1。它们之间的距离是用Hamming距离来计算的，也是就不同的比特位数。我们使用一个很简单的哈希函数族 H ，每一个哈希函数是随机的选择一个特定的比特位上的值， H 包含了所有的从 {0,1}d 映射到 {0,1} 的函数，并且有 hi(p)=pi 。从 H 中随机地选择哈希函数 h ，那么 hi(p) 将会随机地返回 p 的一个比特位。
那么 Pr[h(p)=h(q)] 就等于 p，q 中相同的比特位数的比例，因此有 P1=1−R/d ， P2=1−cR/d ，对于任意的 c>1 ，都满足 P1>P2 。即这种构造出来的哈希函数族是局部敏感的！[1]

Emdedding:

上面讲的一个例子因为数据本身刚好就是二进制，使用的Hamming距离，不需要其他的操作，但是实际上在最开始提出LSH时，是还有一个Embedding操作的。

Original LSH在哈希之前，首先要先将数据从L1准则下的欧几里得空间嵌入到Hamming空间，因为L2准则下的欧几里得空间没有直接的方法嵌入到Hamming空间。在做此Embedding时，有一个假设就是原始点在L1准则下的效果与在L2准则下的效果相差不大，即欧氏距离和曼哈顿距离的差别不大。

Embedding算法：
1. 找到所有点的所有坐标值中的最大值C；
2. 对于一个点P来说，P=(x1,x2,…,xd)，d是数据的维度；
3. 将每一维xi转换为一个长度为C的0/1序列，其中序列的前xi个值为1，剩余的为0.
4. 然后将d个长度为C的序列连接起来，形成一个长度为Cd的序列.

值得说明的是，Embedding操作是保距离的，即在Embedding前后两个点之间的距离是不变的。更多细节可看论文[2]

概率放大：

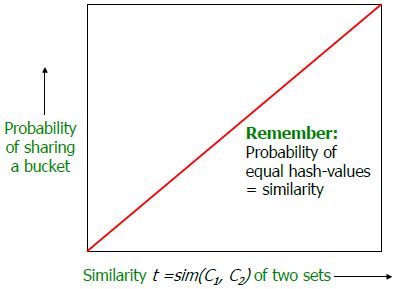
一个哈希函数族的概率 P1，P2 之间的差不够大，通常会通过增加哈希键的长度 k 和哈希表的个数 L 来增加 P1，P2 之间的差。搜索多个哈希表后找出Candidates，然后进行线性搜索，这时只要有一个哈希表能够找到真实近邻就能保证最终能找到近邻。理想的情况是对于距离在 R 以内的点，通过哈希映射后距离为0，对于距离在 cR 以外的点，距离为1（这里1是归一化后的距离）。如何做到这个呢？

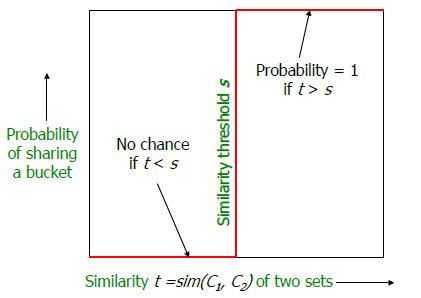
想要的概率曲线

单个哈希的概率曲线

b 个哈希表、哈希键长度为 r 时的概率曲线

我们选择参数 k，L ，有 L 个哈希函数 gj(q)=(h1,j(q),h2,j(q),...,hk,j(q)) ，其中 hk,j(q)(1≤t≤k,1≤j≤L)
若哈希键的长度为 k ，由于哈希函数的选择都是独立随机选择的，对一个每一个哈希函数 gi,Pr[gi(p)=gi(q)]≥Pk1 ，那么使用 L 个哈希表找到真实近邻的概率至少为 1−(1−Pk1)L 。

关于 k，L 的选择说明，可以参考斯坦福课件[3]，这里可以通过一个表简单说一下。如下表所示，当 k=4，L=4 ，对于 p=0.9，1−(1−Pk1)L=0.9860 ，而对于概率较小的 p ，会使其值变得更小，比如对于 p=0.5，1−(1−Pk1)L=0.2275 ，这样的一个变化趋势正是我们想要的！通常在应用中会选择更大的 k，L 。

搜索近似最近邻：

在搜索近似最近邻的时候，按照选择的哈希函数来映射，对于每一个哈希表，选择出落入的哈希桶里的所有节点，对 L 个哈希表都做相同操作，线性搜索所有的candidates。

总结一下，就是如下步骤：

二、Hamming距离

在对图像进行匹配时，通常是将图像的描述子与数据中的图像描述子进行匹配实现的。在实时应用中，通常是使用二进制描述子，比如BIREF、BRISK、ORB等。对于二进制描述子使用的是Hamming距离。下面就介绍关于Hamming距离的局部敏感哈希函数。

正如在上面所说的那样，对于二进制描述子，哈希函数就是直接选择描述子的某一个比特位，通过若干个哈希函数选择出来的位的级联，就形成了一个哈希键了。通过对这个哈希键对数据库中的描述子进行索引，即形成了一个哈希表，选择若干个哈希表来增大找到近似最近邻的概率。

三、Euclidean距离

对于欧式距离，参考 E2LSH ，基于p-stable distribution的LSH（有时间再补上）

四、Jaccard 系数

LSH还可以用来查找相似新闻网页或文章，这时候用来评价两个网页或者文章的相似度的量是Jaccard 系数。

Jaccard系数用来度量两个集合的相似度，值越大值相似度越高。设有两个集合 S1 和 S2 ，它们之间的Jaccard系数定义为：

s=∥S1∩S2∥∥S1∪S2∥

例如 S1=A,B,C，S2=B,C,D ， 则 s=24

上图是一个总体的流程图，分为三步:

第一步就是对一个文档转化为关键词的集合，用这个集合来表示这个文档，叫Shingling。
第二步就是用MinHashing函数来构造哈希表。
第三步就是使用LSH来寻找相似的文档。

这里主要对MinHashing进行介绍。更多细节还是请看斯坦福的课件[3]。

当查询文档时，先Shingling，得到一个文档和词的关系，通常是一个列向量，这个列向量和原数据库的所有列向量一起组成了一个矩阵。可以想象这个矩阵是个很稀疏的高维矩阵，行数是所有的词汇的个数，列数是所有的文档个数。直接用这个高维矩阵进行操作会很耗时，于是就要对其进行压缩，这一步就是MinHashing，然后得到一个维数小得多的Signature矩阵，每一列还是表示一个文档。得到Signature矩阵之后的操作就和前面一样了，使用LSH就可以很快找到相似文档了。

这里有一个很重要的一点，就是在进行MinHashing之后，相似度是保持不变的！正是因为如此才能保证在低维的Signature矩阵找到相似的列在原来的高维矩阵中仍然是相似的。这就保证了这样的哈希函数是局部哈希函数族！

那么MinHashing是怎么做的呢？

上图中白色框中为一个输入矩阵，每一个列表示一个文档，行表示一个关键词。这里哈希函数就是 hπ(C)=minπ(C) 。首先重点内容定义一个变异(Permutation π )，这个变异操作将原来的矩阵的行之间交换。比如从咖啡红表示的第一个变异，其序列值是 {2,3,7,6,1,5,4} ，表示新的矩阵的每一行的行号是原来矩阵的哪一行。然后看变异后的矩阵每一列的第一个1出现在哪一行，行号就是该列元素值。这样操作过后，每一个变异 π 得到一个行向量，如图中所示，咖啡红表示的变异 {2,3,7,6,1,5,4} 得到的行向量为 {2,1,2,1} 。使用N个变异，即可以得到一个N行的矩阵，这个矩阵就是Signature Matrix。

右下角有关于对原矩阵和Signature矩阵的列的相似度的比较，可以看到，两个矩阵的列的相似度很接近。事实上，后面会证明，从概率的意义上这两者会是一样的。

直接定义 π(y)=min(π(C1∪C2)) ，那么 y 要么属于 C1 ，要么属于 C2 。所以 y 同时属于 C1，C2 的概率就是 Pr(y∈C1∩C2) 。也就是说 Pr[min(π(C1)=min(π(C2))]=∥C1∩C2)∥∥C1∪C2)∥ 。

换个角度理解，对于 C1，C2 的行分为三种：

1. 类 X : 两个列的值都是1；
2. 类 Y : 一列是1，另一列是0；
3. 类 Z : 两个列的值都是0；

由于是稀疏矩阵，所以绝大多数是 Z 类别。变异后随机排列行，那么从上到下在遇到类 Y 之前遇到类 X 的概率是 ∥X∥∥X+Y∥ ，首先遇到的列类型是 X ，说明 min(hπ(C1))=min(hπ(C2)) 。又有 ∥X∥=∥C1∩C2∥ ， ∥X+Y∥=∥C1∪C2∥ ，所以可以得到 ∥X∥∥X+Y∥=∥C1∩C2)∥∥C1∪C2)∥ 。也同样可以得到 Pr[min(π(C1)=min(π(C2))]=∥X∥∥X+Y∥=∥C1∩C2)∥∥C1∪C2)∥ 。

对于式子 Pr[min(π(C1)=min(π(C2))]=∥C1∩C2)∥∥C1∪C2)∥ ，右边就是 C1，C2 的Jaccard系数！即证明了 Pr[min(π(C1)=min(π(C2))]=sim(C1,C2)

到现在完成了第一步了。后面对于Signature矩阵的操作就和之前讲的类似了。本质上都是通过AND和OR操作来提升概率差，得到我们想要的概率曲线。不过具体实现方式稍微有点不同。

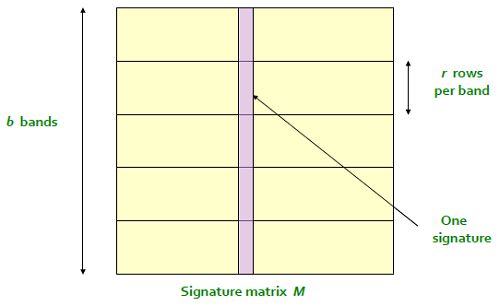
首先通过很多变异操作得到一个足够大的Signature矩阵，然后对这个矩阵进行划分，每 r 个行构成一个Band，总共有 b 个Bands，也就是说总共进行了 r∗b 次变异操作，得到了一个行数为 r∗b 的Signature矩阵。使用上面提到的MinHashing对每一个band单独进行哈希，就得到了 b 个哈希表。

五、参考资料:

[1] Andoni A, Indyk P. Near-Optimal Hashing Algorithms for Approximate Nearest Neighbor in High Dimensions.
[2] Gionis A, Indyk P, Motwani R. Similarity search in high dimensions via hashing.
[3] Stanford CS246 关于LSH的章节 http://cs246.stanford.edu
[4] Datar M, Immorlica N, Indyk P, et al. Locality-sensitive hashing scheme based on p-stable distributions.
[5] E2LSH user manual
[6] Slaney M, Casey M. Locality-Sensitive Hashing for Finding Nearest Neighbors [Lecture Notes]