牛客网暑期ACM多校训练营（第五场）E room 带权二部图匹配问题（费用流解决）

链接：https://www.nowcoder.com/acm/contest/143/E
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld
题目描述
Nowcoder University has 4n students and n dormitories ( Four students per dormitory). Students numbered from 1 to 4n.

And in the first year, the i-th dormitory ‘s students are (x1[i],x2[i],x3[i],x4[i]), now in the second year, Students need to decide who to live with.

In the second year, you get n tables such as (y1,y2,y3,y4) denote these four students want to live together.

Now you need to decide which dormitory everyone lives in to minimize the number of students who change dormitory.

输入描述:
The first line has one integer n.

Then there are n lines, each line has four integers (x1,x2,x3,x4) denote these four students live together in the first year

Then there are n lines, each line has four integers (y1,y2,y3,y4) denote these four students want to live together in the second year
输出描述:
Output the least number of students need to change dormitory.
示例1
输入
复制
2
1 2 3 4
5 6 7 8
4 6 7 8
1 2 3 5
输出
复制
2
说明
Just swap 4 and 5
备注:
1<=n<=100

1<=x1,x2,x3,x4,y1,y2,y3,y4<=4n

It’s guaranteed that no student will live in more than one dormitories.

题意：有N个宿舍，每个宿舍都分配了4个人。然后下一年可以自由结合组合宿舍，然后给出了列表，表示现在他们希望的住宿。问你最少需要交换宿舍的人数。比如1,2,3,4原来住在一起，现在他们仍希望住在一起，就不需要有人交换。(可以安排到不同的宿舍，是不认为被交换的，比如原来他们住1号，现在住3号，但仍是他们四个，则没有人被交换）

思路：假如固定现在宿舍的编号对于样例就是固定1号为4,6,7,8四个人。2号就是1，2，3，5四个人。考虑原来每个宿舍搬到现在其他所有宿舍需要交换的人数，即建立一条边。这样就构成了一个二部图，如果考虑最多不用搬离宿舍的人数。这样就是一个带权二部图的最大匹配。不过这里直接考虑最少交换人数用最小费用流就可以了。
建图如下:

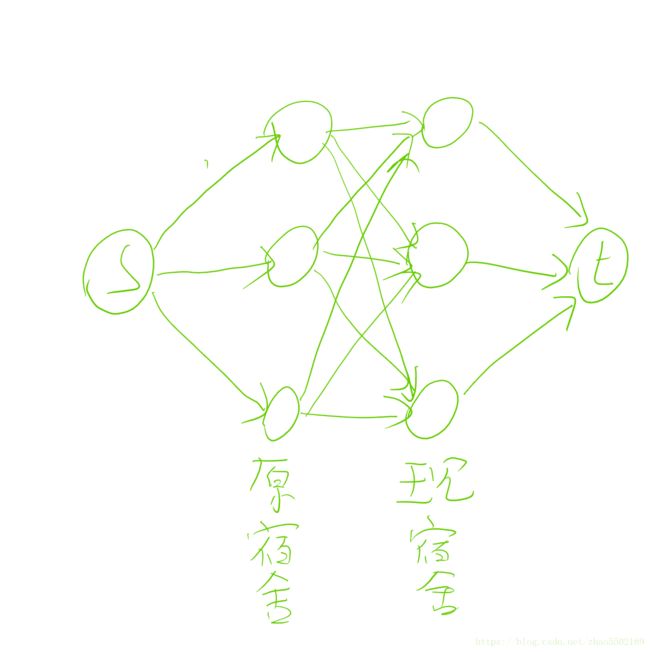
s到点和点到t都是cap = 1,cost = 0，点之间的权值是cap = 1,cost = 最少交换人数。这样求s到t的流量为N的最小cost就可以了
代码如下:

#include

using namespace std;
const int MAX = 210;
const int INF = 0x3f3f3f3f3f;
class Edge{
public:
    int to,cap,cost,rev;
    Edge();
    Edge(int _to,int _cap,int _cost,int _rev);
};
int V;
vector G[MAX];
int dis[MAX];
int prevv[MAX],preve[MAX];
void add_Edge(int from,int to,int cap,int cost){
    G[from].push_back(Edge(to,cap,cost,(int)G[to].size()));
    G[to].push_back(Edge(from,0,-cost,(int)G[from].size()-1));
}

int min_cost_flow(int s,int t,int f){
    int res = 0;
    while(f > 0){
        fill(dis,dis+V,INF);
        dis[s] = 0;
        queue<int> que;
        que.push(s);
        while(!que.empty()){
            int v = que.front();que.pop();
            for(int i=0;iif(e.cap > 0 && dis[e.to] > dis[v] + e.cost){
                    dis[e.to] = dis[v] + e.cost;
                    prevv[e.to] = v;
                    preve[e.to] = i;
                    que.push(e.to);
                }
            }
        }
        if(dis[t] == INF){
            return -1;
        }
        int d = f;
        for(int v = t;v != s; v = prevv[v]){
            d = min(d,G[prevv[v]][preve[v]].cap);
        }
        f -= d;
        res += d*dis[t];
        for(int v=t;v != s;v = prevv[v]){
            Edge &e = G[prevv[v]][preve[v]];
            e.cap -= d;
            G[v][e.rev].cap += d;
        }
    }
    return res;
}
int x[MAX][4],y[MAX][4];
//求y[v]与x[u]中相同的个数.
int GetHave(int u,int v){
    int res = 0;
    for(int i=0;i<4;++i){
        for(int j=0;j<4;++j){
            if(y[v][j] == x[u][i]){
                res++;
                break;
            }
        }
    }
    return res;
}
int main(void){
    int N;
    cin >> N;
    V = 2*N+2;
    int s = 0,t = 2*N+1;
    for(int i=1;i<=N;++i){
        cin >> x[i][0] >> x[i][1] >> x[i][2] >> x[i][3];
        add_Edge(s,i,1,0);
    }
    for(int i=1;i<=N;++i){
        cin >> y[i][0] >> y[i][1] >> y[i][2] >> y[i][3];
        add_Edge(N+i,t,1,0);
    }
    for(int i=1;i<=N;++i){
        for(int j=1;j<=N;++j){
            add_Edge(i,N+j,1,4-GetHave(i,j));//4-相同人数就是需要交换的人数
        }
    }
    cout << min_cost_flow(s,t,N) << endl;
    return 0;
}
Edge::Edge(){
    to = cap = cost = rev = 0;
}
Edge::Edge(int _to,int _cap,int _cost,int _rev){
    to = _to;
    cap = _cap;
    cost = _cost;
    rev = _rev;
}