小波变换一之Haar变换

Haar变换

案例一简单一维信号变换

下面是一个一维信号（一组数）：$f=\{2,2,2,4,4,4\}$

我对这个信号进行如下处理：

$a_m=\sqrt{2}\frac{f_{2m-1}+f_{2m}}{2}=\frac{f_{2m-1}+f_{2m}}{\sqrt{2}}$（相邻两个数相加，求平均，然后乘以$\sqrt{2}$）

$d_m=\sqrt{2}\frac{f_{2m-1}-f_{2m}}{2}=\frac{f_{2m-1}-f_{2m}}{\sqrt{2}}$（相邻两个数相减，求平均，然后乘以$\sqrt{2}$）

注：至于为什么要乘以$\sqrt{2}$呢？我们这里先不解释，放到后面再说。

然后按照先$a$后$d$的顺序排列$a_1,a_2,...,a_{N/2},d_1,d_2,...,d_{N/2}$（$N$是离散信号中的值的个数）

则，$a=\{2\sqrt{2},3\sqrt{2},4\sqrt{2}\}$，$d=\{0,-\sqrt{2},0\}$

我们可以得到结果：$tf=\{2\sqrt{2},3\sqrt{2},4\sqrt{2},0,-\sqrt{2},0\}$

这就是传说中的Haar变换了……

$a$表示的是信号的趋势（trend），近似（approximation），是低频信息；而$d$表示的是信号的细节（detail），是高频信息。

那么我们怎么变回去呢？我们对变换以后的信号进行如下处理：

$f_{2m-1}=\sqrt{2}\frac{a_m+d_m}{2}=\frac{a_m+d_m}{\sqrt{2}}$（第$m$个$a$和$d$相加，求平均，然后乘以$\sqrt{2}$）

$f_{2m}=\sqrt{2}\frac{a_m-d_m}{2}=\frac{a_m-d_m}{\sqrt{2}}$ （第$m$个$a$和$d$相减，求平均，然后乘以$\sqrt{2}$）

我们可以得到结果$if=\{2,2,2,4,4,4\}$

这样就是Haar变换的逆变换。

通过观察，我们可以发现：

• $d$中的数字绝大部分都很小（这是做信息压缩很重要的依据）
• 变换前后信号的能量保持不变，即$\sum f_i^2=\sum a_m^2+\sum d_i^2$（有兴趣的同学可以算一下对于$f$和$tf$的能量都是60，刚好相等）

案例二多分辨率一维信号变换

我们可以按照上面的思路将信号对得到的低频信号（$a$）一直一直划分下去，直到${\mathrm{l}\mathrm{o}\mathrm{g}}_{2}N$（离散信号的值的数目不是偶数的，可以在后面补0）

给定如下的一个信号：$f(t)=20x^2(1-x{)}^4\cos (12\pi x)$

我们通过在[0, 1]之间取样1024个点可以得到信号的振幅，绘制出信号图像如下：

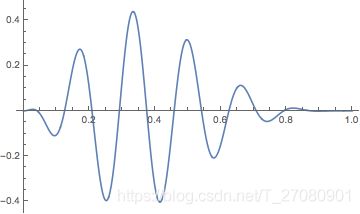
我们可以通过案例一种描述的方法进行Haar变换，我们这里对$f(t)$信号进行两次Haar变换，如下图所示：

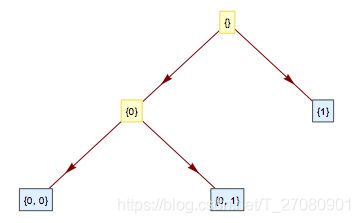
这是多分辨率分析（Multi-Resolution Analysis，MRA）以及图像压缩（JPEG2000编码）等的基础理念，这里现有一个大概理解，后面我们会继续谈到。

变换的结果如下（感兴趣的朋友可以使用Mathematica或者MATLAB是一样，这两个数学软件都提供了对Haar变换的直接支持）：

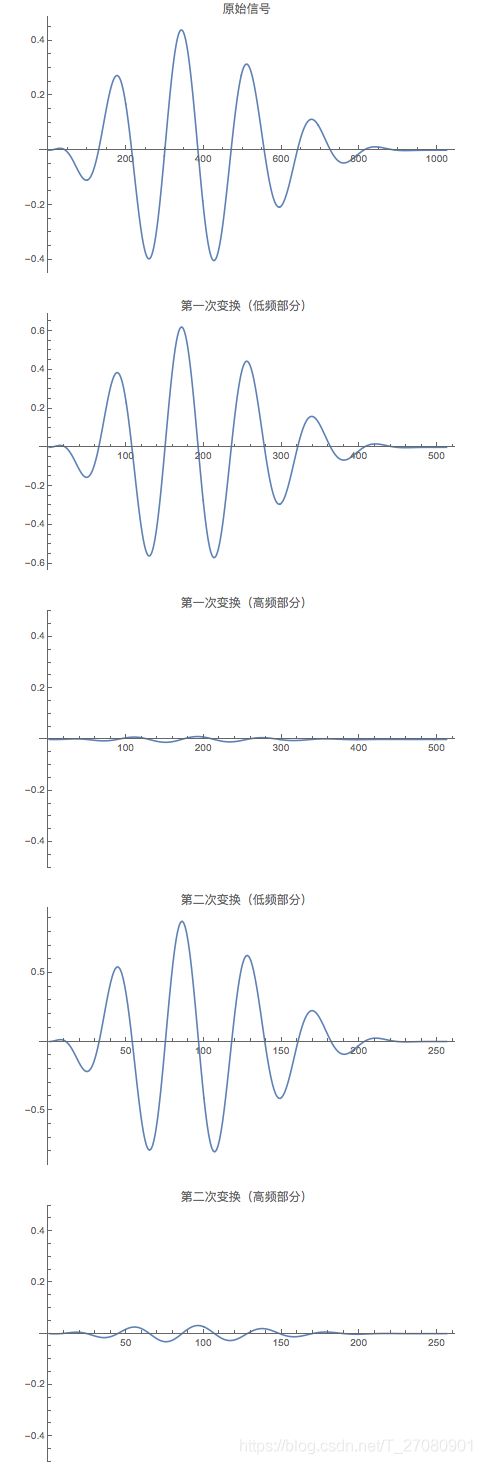
好了，这一节先到这里，我们以后有时间慢慢聊！