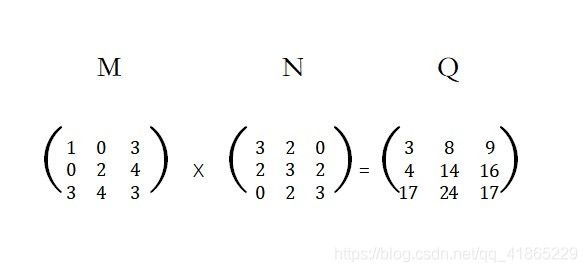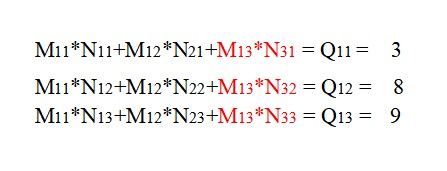(五)1.1_稀疏矩阵乘法的快速运算
一.问题描述
有矩阵M和N,都是用三元组压缩存储,设计高效率算法求矩阵M*N得到的矩阵Q(也用三元组压缩存储).
二.思路分析
假设矩阵M*N=Q 如下
那么得到的矩阵Q有三行三列,第一行中的元素有这样的关系
所以我们可以这样,在遍历到M11时,由于N11,N12,N13是在顺序表中连续排列的,所以我们可以创建一个3个累加器(int QElem[4]={0}),
遍历到M11时,先算Q11,Q12,Q13的第一项,累加到累加器中即
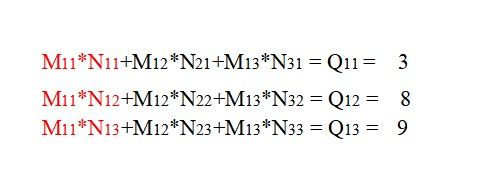
QElem[1]+=M11*N11,
QElem[2]+=M11*N12,
QElem[3]+=M11*N13,
然后遍历到M12时计算第二项,累加到累加器中即
QElem[1]+=M12*N21,
QElem[2]+=M12*N22,
QElem[3]+=M12*N23,
接着遍历到M13时计算第三项,累加到累加器中即
QElem[1]+=M13*N31,
QElem[2]+=M13*N32,
QElem[3]+=M13*N33,
这样Q中第一行的元素就计算出来了,我们把累加器里的值存到Q矩阵的顺序表中就ok了
接着重复上述步骤,遍历M矩阵的第2行元素,第三行也是同理
这样每行M中的元素只需遍历一次,就能计算出M乘以N得到得矩阵Q了,效率比普通算法更高
三.代码实现
这里来看一下代码的具体实现,注意这个算法需要一个附加信息,也就是矩阵每行第一个非零元素在顺序表中的位置序号,这个信息是为了能够准确遍历矩阵中的某行所有元素
#include"stdio.h"
#include"stdlib.h"
#define MAXSIZE 2000
//线性表0单元不用是为了便于理解程序
//元素类型
typedef int SqPosType;
typedef struct
{
int i; //行
int j; //列
SqPosType e; //元素
}Triple; //三元组
typedef struct
{
int mu,nu,tu; //矩阵的行数,列数,非零元素的数量
int SqPos[10]; //每行非零元素在顺序表(data)中的位置,SqPos[0]未用
Triple data[MAXSIZE+1]; //非零单元三元组表,data[0]未用
}RLSMatrix;
RLSMatrix M=
{
3,3,7,{0,1,3,5},
{
{0,0,0},
{1,1,1},
{1,3,3},
{2,2,2},
{2,3,4},
{3,1,3},
{3,2,4},
{3,3,3},
}
};
RLSMatrix N=
{
3,3,7,{0,1,3,6},
{
{0,0,0},
{1,1,3},
{1,2,2},
{2,1,2},
{2,2,3},
{2,3,2},
{3,2,2},
{3,3,3},
}
};
//矩阵相乘算法
void MultSmatrix(RLSMatrix M,RLSMatrix N,RLSMatrix &Q)
{
Q.mu=M.mu; //相乘得到的矩阵的行数等于矩阵M的行数
Q.nu=N.nu; //相乘得到的矩阵的列数等于矩阵N的列数
Q.tu=0; //相乘得到的矩阵的元素数量暂时未知,暂定为0
int M_row,N_row; //矩阵M,N的元素的行位置(在矩阵中)
//遍历存储M矩阵的所有行
for(M_row=1;M_row<=M.mu;M_row++)
{
int QElem[Q.nu+2]={0}; //一行中每列的元素的累加器
Q.SqPos[M_row]=Q.tu+1; //相乘得到的矩阵每行非零元素在顺序表中的位置
int SqPos2_M; //遍历到M矩阵的元素的下一行非零元素在顺序表中的位置
//为了找出相同行的元素在顺序表中的位置范围
if(M_row<M.mu)
SqPos2_M=M.SqPos[M_row+1]; //当前行的下一行非零元素在顺序表中的位置
else
SqPos2_M=M.tu+1; //当前行的下一行非零元素在顺序表中的位置,因为M_row+1超界了,所以用尾元素位置加一
int SqPos_M; //矩阵N中被遍历到的元素在顺序表中的位置
//遍历M矩阵中一行中的所有元素
for(SqPos_M=M.SqPos[M_row];SqPos_M<SqPos2_M;SqPos_M++)
{
N_row=M.data[SqPos_M].j; //通过M中元素的列位置,找到N中对应元素的行位置,M中a元素要乘以N中元素b;a b的关系是a在M中的列位置是b在N中的行位置
int SqPos2_N; //遍历到N矩阵的元素的下一行非零元素在顺序表中的位置
//为了找出相同行的元素在顺序表中的位置范围,其实作用为了遍历一行中的所有非零元素
if(N_row<N.mu)
SqPos2_N=N.SqPos[N_row+1]; //当前行的下一行非零元素在顺序表中的位置
else
SqPos2_N=N.tu+1; //当前行的下一行非零元素在顺序表中的位置,因为N_row+1超界了,所以用尾元素位置加一
int SqPos_N; //矩阵N中被遍历到的元素在顺序表中的位置
//遍历N矩阵中一行中的所有元素
for(SqPos_N=N.SqPos[N_row];SqPos_N<SqPos2_N;SqPos_N++)
{
int col=N.data[SqPos_N].j; //Q矩阵元素的列位置等于N矩阵的元素的列位置
QElem[col]+=M.data[SqPos_M].e*N.data[SqPos_N].e; //用累加器累加各一行中各列的元素的结果
}
}//for SqPos_M
//M中的一行元素已经和N中所有列的元素计算完了,现在遍历累加器中的元素,将计算得到的Q中一行的元素存入顺序表
for(int col=1;col<=Q.nu;col++)
{
if(QElem[col]!=0) //非零元素
{
++(Q.tu); //非零元素数量加一
Q.data[Q.tu]={M_row,col,QElem[col]}; //非零元素存入Q矩阵的顺序表
}
}//for col
}//for M_row
}
//显示三元组
void Print(RLSMatrix M)
{
int m=M.mu; //矩阵行数
int n=M.nu; //矩阵列数
int t=M.tu; //矩阵非零元素个数
printf("\n\n i j e\n\n");
for(int i=1;i<=t;i++)
{
printf("%4d%4d%4d\n",M.data[i].i,M.data[i].j,M.data[i].e); //显示三元组的三个元素
}
}
int main()
{
RLSMatrix Q; //初始化相乘后的矩阵Q
MultSmatrix(M,N,Q); //把矩阵M和矩阵N相乘得到矩阵赋值给矩阵Q
printf("\n矩阵M:\n");
Print(M);
printf("\n矩阵N:\n");
Print(N);
printf("\n矩阵Q=M*N:\n");
Print(Q); //显示Q矩阵的三元组
return 0;
}
操作结果:
四.算法概述
1.可以看到这里定义的存储矩阵三元组的结构体,还要存储矩阵每行第一个非零元素在顺序表中的位置序号,这是为了能够准确的遍历到矩阵某一行的所有元素
注意:我们为了更好的理解这个算法,所以很多数组零单元都是不使用的
2.算法中有3个层次的循环,第1层循环是依次遍历矩阵M的行,第2层循环是遍历M矩阵某行中的所有元素,第3层循环是遍历N矩阵中某行的所有元素,并分别与第2层循环遍历的M中的某个元素相乘然后结果分别加到Q的累加器中.
3.第2层循环有两个同层次的循环,
先进行遍历M某行所有元素的循环,通过累加器.计算出Q中某行所有元素的值.
然后我们再通过一个循环把累加器里的值存储到Q矩阵的顺序表