算法设计与分析复习笔记(上)
简介:本文是博主在复习算法设计与分析的笔记,参考了北大算法设计与分析以及王晓东编著的《计算机算法设计与分析》第四版相关内容,如有错误,欢迎指正。
文章目录
- 设计技术
-
- 分治
- 动态规划
设计技术
分治
| 使用条件 | 规约为独立求解子问题 |
|---|---|
| 设计步骤 | 规约方法,初始子问题的计算,子问题解的综合方法,注意子问题划分均衡,类型相同 |
| 递归算法分析 | 求解递推方程 |
| 改进途径 | 减少子问题数,预处理 |
| 典型问题 | 二分检索,归并排序,芯片测试,幂乘,矩阵乘法,最邻近点对,多项式求值 |
代码
例1:阶乘函数
int facorial(int n)
{
if(n==0) return 1;
return n*facorial(n-1);
例2:fibonacci数列
int fibonacci(int n)
{
if(n<=1) return 1;
return fibonacci(n-1)+fibonacci(n-2);
}
例3:排列问题
template<class Type>
void Perm(Type list[],int k,int m)
{
//产生list[k,m]的所有排列
if(k==m)
{
//只剩下一个元素
for(int i-0;i<=m;i++)cout<<list[i];
cout<<endl;
}
else//将list[k:m]中的每个元素分别与list[k]中的元素进行交换,
然后递归计算list[k+1:m]的全排列
{
for(int i=k;i<=m;i++)
{
Swap(list[k],list[i]);
Perm(list,k+1,m);
Swap(list[k],list[i]);
}
}
template<class Type>
{
inline void Swap(Type &a,Type &b)
{
Type temp=a;
a=b;
b=temp;
}
}
例4:整数划分问题
int q(int n,int m)//n为要划分的整数,将最大加数n1<=m的划分个数记做q(n,m)
{
if((n<1)||(m<1))return 0;
if((n==1)||(m==1))return 1;
//最大加数不超过1
if(n<m) return q(n,n);//最大加数大于n
if(n==m)return q(n,m-1)+1;//q(n,n)=q(n,n-1)+1;1是n1=n的划分个数
return q(n,m-1)+q(n-m,m)//假设分解6(n)的最大加数不超过3(m),这个划分个数=最大加数不超过2的划分个数(因为可能会有最大加数为1的,所以不能用n-m作为第一个参数)+最大加数是3的划分个数(把3再划分为最大加数不超过6-3=3的划分个数,即3个)
}
例5:Hanoi塔问题
void hanoi(int n,int a,int b,int c)//n是圆盘个数,a,b,c表示塔座
{
//把塔座a的圆盘移动到塔座b上,c为辅助塔座
if(n>0)
{
hanoi(n-1,a,c,b);//把塔座a的n-1个圆盘移动到塔座c上,以塔座b为辅助塔座
mov(a,b);//将a上编号为n的圆盘移到b上
hanoi(n-1,c,b,a);//将塔座c的n-1个圆盘移动到塔座b上,以塔座a为辅助塔座
}
}
分治法的基本思想
divide and conquer(P)
{
if(|P|<=n0)adhoc(P);问题P的规模不超过n0时,直接解小规模问题P
divide P into smaller subinstances P1,P2...Pk
for(i=1;i<=k;i++)
yi=divide and conquer(Pi);
return merge(y1,y2,..yk);//归并解
}
例6:二分搜索算法
template <class Type>
int BinarySearch(Type a[],const Type &x,int n)
{
//在a[0]-a[n-1]中找x
int left=0;int right=n-1;
while(left<=right)
{
int middle=(left+right)/2;
if(x==a[middle])return middle;
if(x>a[middle]) left=middle+1;
else right=middle-1;
}
return -1;
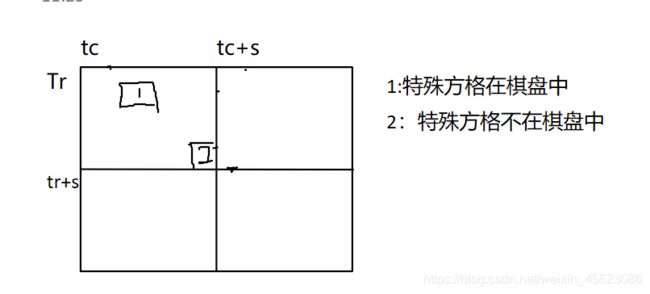
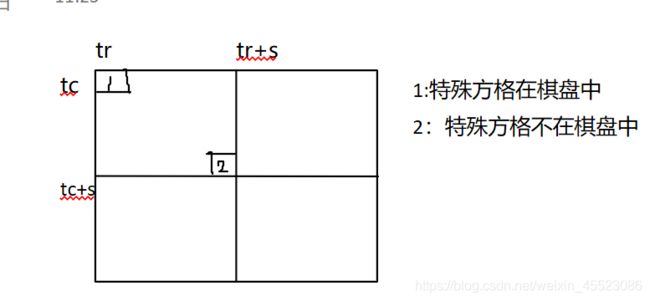
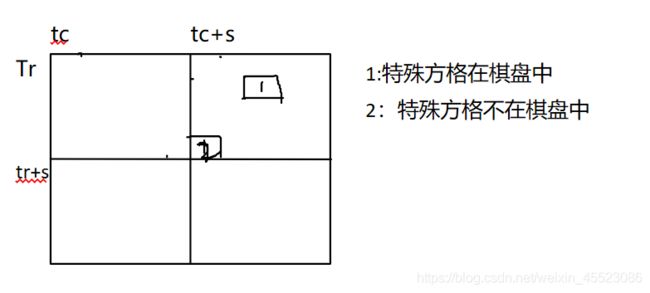
例7:棋盘覆盖
void ChessBoard (int tr,int tc,int dr,int dc,int size)
{
//棋盘左上角的坐标(tr,tc),特殊方格的坐标(dr,dc),size=2^K,棋盘规格2^K*2^K
if(size==1) return;//棋盘规格为1*1
int t=tile++;//L型骨牌号
s=size/2;//分割棋盘
//覆盖左上角子棋盘
if(dr<tr+s&&dc<tc+s)//特殊方格在此棋盘中
ChessBoard(int tr,tc,dr,dc,s);
else//此棋盘无特殊方格
{
//用t号L型骨牌覆盖右下角
Board[tr+s-1][tc+s-1]=t;
//覆盖其他方格
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);//以刚才L型骨牌覆盖的方格作为特殊方格进行继续覆盖
}
//覆盖右上角子棋盘
if(dr<tr+s&&dc>=tc+s)
//特殊方格在此棋盘中
ChessBoard(tr,tc+s,dr,dc,s);
else{
//此棋盘中无特殊方格
Board[tr+s-1][tc+s]=t;
ChessBoard(tr,tc+s,tr+s-1,tc+s,s);}
//覆盖左下角子棋盘
if(dr>=tr+s&&dc<tc+s)
ChessBoard(tr+s,tc,dr,dc,s);
else{
Board[tr+s][tc+s-1]=t;
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);}
//覆盖右下角子棋盘
if(dr>=tr+s&&dc>=tc+s)
ChessBoard(tr+s,tc+s,dr,dc,s);
else{
Board[tr+s][tc+s]=t;
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
例8:合并排序
template<class Type>
void MergeSort(Type a[],int left,int right)
{
if(left<right){
//至少2个元素
int i=(left+right)/2;//取中点
MergeSort(a,left,i);
MergeSort(a,i+1;right);
Merge(a,b,left,i,right);//合并到数组b
Copy(a,b,left,right);//复制回数组a
}
}
template<class Type>
void MergeSort(Type a[],int left,int right)
{
Type *b=new Type[n];
int s=1;
while(s<n){
MergePass(a,b,s,n);//合并到数组b
s+=s;
MergePass(b,a,s,n);//合并到数组a
s+=s;
}
}
template<class Type>
void MergePass(Type x[],Type y[],int s,int n)
{
int i=0;//合并大小为s的相邻子数组
while(i<=n-2*s){
//合并大小为s的相邻2段子数组
Merge(x,y,i,i+s-1,i+2*s-1);
i=i+2*s;
}
//剩下的元素个数少于2*s
if(i+s<n)Merge(x,y,i+s-1,i+2*s-1);
else for(int j=i;j<=n-1;j++)
y[j]=x[j];
}
template<class Type>
void Merge(Type c[],Type d[],int l,int m,int r)
{
//合并c[l:m]和c[m+1:r]到d[l:r]
inti=l,j=m+1,k=l;
while(i<=m&&j<=r)
if(c[i]<=c[j])d[k++]=c[i++];//按顺序排好了直接复制
else d[k++]=c[j++];//否则继续合并
if(i>m) for(int q=i;q<=r;q++)d[k++]=c[q];
else for(int q=i;q<=m;q++)d[k++]=c[q];
}
例9:快速排序
template<class Type>
void QuickSort(Type a[],int p,int r)
{
if(p<r)
{
int q=Partition(a,p,r);
QuickSort(a,p,q-1);
QuickSort(a,q+1,r);
}
}
template<class Type>
void Partition(Type a[],int p,int r)
{
int i=p,j=r+1;
Type x=a[p];划分基准
//
//>x的元素交换到右边区域
while(true)
{
//开始i在最左边,j在最右边+1,i不断增加,j不断减少,直到a[i]<=x<=a[j],如果i
while(a[++i]<x&&i<r)
while(a[--i]>x)
if(i>=j)break;
Swap(a[i],a[j]);
a[p]=a[j];
a[j]=x;
return j;返回划分点q=j
)
例10:芯片测试
void test(n)
k<-n;
while k>3 do
芯片分为下取整(k/2)组,轮空处理
for i=1 to 下取整(k/2) do
if 2 片好 then 取任意1片留下
else 2片同时扔掉
k<-剩下的芯片数
if(k==3) then
任取2片芯片测试
if 1好1坏 then 取没测的芯片肯定是好芯片
else 任取一片被测芯片,此时肯定有2片好的,随便取1片
if k==2 or 1 then 任取1片,此时好芯片比坏芯片至少多1片
例11:最接近点对问题
一维
bool Cpair1(S,d)
{
n=|S|;
if(n<2){
d=infinite;return false;}
m=S中各点坐标的中位数
构造S1,S2
Cpairl(S1,d1);
Cpairl(S2,d2);
p=max(S1);//S1的最大点
q=min(S2);//S2的最小点,他们的距离可能是最小距离
d=min(d1,d2,q-p);
return true;
}
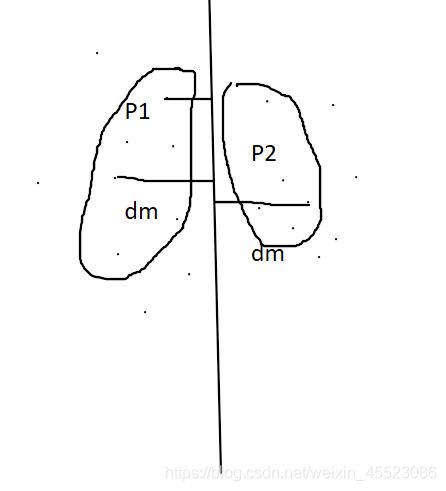
二维
bool Cpair2(S,d)
{
n-|S|;
if(n<2){
d=infinite;return false;}
m=S中各点坐标的中位数
构造S1,S2
Cpair2(S1,d1);
Cpair2(S2,d2);
dm=min(d1,d2);
将P1,P2点按y坐标值排序
扫描X以及对于X的每个点检查Y中与其距离在在dm之内的所有点(最多6个)
d=min(dm,dl);
return true;
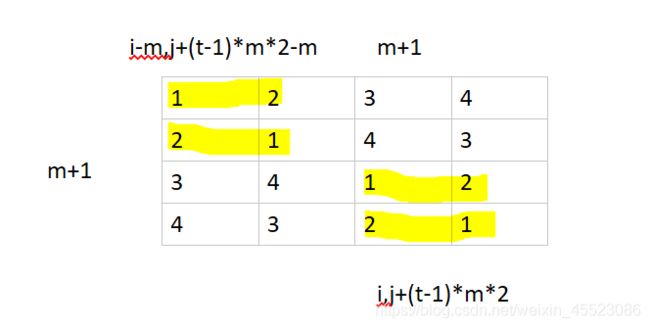
例12:循环赛日程表
void Table(int k,int **a)//有n=2^k个运动员要比赛
{
int n=1;
for(int i=1;i<=k;i++)n*=2;
for(int i=1;i<=n;i++) a[1][i]=i;//给第一个运动员匹配
int m=1;
for(int s=1;s<=k;s++){
n/=2;//把n分成2份,n个选手的比赛日程表可以通过n/2个选手的比赛日程来决定,直到只剩2个选手
for(t=1;t<=m;t++){
for(int i=m+1;i<=2*m;i++){
for(int j=m+1;j<=2*m;j++)
{
a[i][j+(t-1)*m*2]=a[i-m][j+(t-1)*m*2-m];
a[i][j+(t-1)*m*2-m]=a[i-m][j+(t-1)*m*2];
}
m*=2;}
}
动态规划
| 使用条件 | 优化问题,多步判断,求解,满足优化原则,子问题重叠 |
|---|---|
| 设计步骤 | 确定子问题边界,列关于目标函数的递推方程及初值,自底向上,备忘录存储,标记函数及解的追踪方法 |
| 复杂度分析 | 备忘录,递推方程 |
| 典型问题 | 矩阵链相乘,投资,背包,最长公共子序列,图像压缩,最大子段和,最优二分检索树,生物信息学应用 |
例题代码
例1:矩阵连乘
计算2个矩阵乘积的标准算法
void matrixMultiply(int **a,int **b,int **c,int ra,int ca,int rb,int cb)
//ra,ca和rb,cb是矩阵A,B的行数和列数
{
if(ca!=rb)error("矩阵不可乘");
//A矩阵的列数与B矩阵的行数相等
for(int i=0;i<ra;i++)//a的行
{
for(int j=0;j<cb,j++)//b的列
{
int sum=a[i][0]*b[0][j];//第一个数
for(int k=1;k<ca;k++)//列
sum+=a[i][k]*b[k][j];//a的列与b的行相乘的总和
c[i][j]=sum;//给c数组赋值
}
}
}
假设A的维数是p*r,B的维数是r*q,A*B的维数是p*q,需要pqr次数乘
动态规划解矩阵链相乘
void MatrixChain(int *p,int n,int **m,int **s)
//p为每个矩阵的行数和列数,不重复,n为矩阵个数,
//m为矩阵相乘需要的最少乘次数,问题最优值为m[1][n],
//s为对应于m[i][j]的断开位置k
{
for(int i=1;i<=n;i++)m[i][i]=0;//单一矩阵
for(int r=2;r<=n;r++)//扩展链长
for(int i=1;i<n-r+1;i++)//确定每一段开始的矩阵
{
int j=i+r-1;//确定每一段最后的矩阵
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
//设在i和i+1处断开,每个矩阵Ai的维数为p[i-1]*p[i]
//A[i+1]*..A[j]后得到一个维数为p[i]*p[j]的矩阵,与A[i]相乘,计算量为p[i-1]*p[i]*p[j]
s[i][j]=i;//断点在i处
for(int k=i+1;k<j;k++)
{
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
//一个维数是p[i-1]*p[k]的矩阵与一个维数是p[k]*p[j]的矩阵相乘
if(t<m[i][j]){
m[i][j]=t;s[i][j]=k;}
//更新最小计算量和断点
}
}
}
输出计算A[i][j]的计算次序
void Traceback(int i,int j,int **s)
{
//s[1][n]是A[1][n]的最佳断点
if(i==j) return;
Traceback(i,s[i][j],s);
Traceback(s[i][j]+1,j,s);
//在s[i][j]中找断点
cout<<"Multiply A"<<i<<","<<s[i][j];
cout<<"and A"<<(s[i][j]+1)<<","<<i<<endl;//只要调用Traceback(1,n,s)就可以输出最优计算次序
}
备忘录方法解矩阵连乘问题
int MemoizedMatrixChain(int n,int **m,int **s)
{
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)m[i][j]=0;
return LookupChain(1,n);
}
int LookupChain(int i,int j)
{
if(m[i][j]>0)return m[i][j];//存储的是所要求子问题的计算结果
if(i==j)return 0;
int u=LookupChain(i,i)+LookupChain(i+1,j)+p[i-1]*p[i]*p[j];
//断点为i
s[i][j]=i;
for(int k=i+1;k<j;k++)
{
int t=LookupChain(i,k)+LookupChain(k+1,j)+p[i-1]*p[k]*p[j];
if(t<u){
u=t;s[i][j]=k;}//断点为k
}
m[i][j]=u;
return u;
}
例2:最长公共子序列
void LCSLength(int m,int n,char *x,char *y,int **c,int **b)
{
//m为x的元素个数,n为y的元素个数,c存储x[i]和y[j]的最长子序列的长度,
//b记录c的值是由哪个子问题的解得到的
int i,j;
for(int i=1;i<=m;i++)c[i][0]=0;
//当i=0,j=0时空序列是x和y的最长公共子序列
for(int i=1;i<=n;i++)c[0][i]=0;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++){
if(x[i]==y[j]){
c[i][j]=c[i-1][j-1]+1;b[i][j]=1;}
//x和y有一个元素相同
else if(c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];b[i][j]=2;}
//找出x[m-1]和y的一个最长公共子序列及x和y[n-
//1]的一个最长公共子序列,较长者为最长公共子序列
else {
c[i][j]=c[i][j-1];b[i][j]=3;}
}
}
根据b的内容打印出最长公共子序列
void LCS(int i,int j,char *x,int **b)
{
if(i==0||j==0)return;
if(b[i][j]==1){
LCS(i-1,j-1,x,b);cout<<x[i];}
else if(b[i][j]==2){
LCS(i-1,j,x,b);
else LCS(i,j-1,x,b);
}
例3:最大子段和
分治算法
int MaxSubSum(int *a,int left,int right)
{
//把数组分成长度相等的2半,分别求这两半的最大子段和
int sum=0;
if(left==right)sum=a[left]>0?a[left]:0;
//数组只有一个元素,当所有整数都为负数时规定最大子段和为0
else{
int center=(left+right)/2;
int leftsum=MaxSubSum(a,left,center);
int rightsum=MaxSubSum(a,center+1,right);
int s1=0;
int lefts=0;
for(int i=center;i>=left;i--)
{
//从中间向左边找最大子段
lefts+=a[i];
if(lefts>s1) s1=lefts;
}
int s2=0;
int rights=0;
for(int j=center+1;j<=right;j++)
{
//从中间向右边找最大子段
rights+=a[i];
if(rights>s2)s2=rights;
}
sum=s1+s2;
if(sum<leftsum)sum=leftsum;
if(sum<rightsum)sum=rightsum;}
return sum;
}
int MaxSum(int n,int *a)
{
return MaxSubSum(a,1,n);
}
动态规划算法
int MaxSum(int n,int *a)
{
int sum=0,b=0;//b为i-j的最大子段和
for(int i=1;i<=n;i++)
{
if(b>0)b+=a[i];//如果前i-1的子段和大于0,继续累加
else b=a[i];//前i-1的子段和小于0,令b从a[i]开始累加
if(b>sum)sum=b;//和当前最优解比较
}
return sum;
}
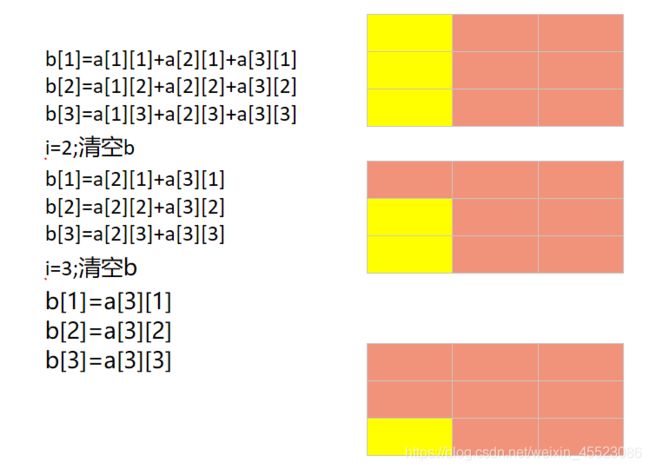
最大子矩阵和问题:矩阵A的维数m*n,求子矩阵使各元素之和达到最大
int MaxSum2(int m,int n,int **a)
{
int sum=0;
int *b=new int[n+1];
for(int i=1;i<=m;i++){
for(int k=1;k<=n;k++)b[k]=0;
for(int j=i;j<=m;j++){
for(int k=1;k<=n;k++)b[k]+=a[j][k];
int max=MaxSum(n,b);
if(max>sum)sum=max;
}
}
return sum;
}
最大m子段和问题
int MaxSum(int m,int n,int *a)
{
if(n<m||m<1)return 0;//
int *b=new int[n+1];//数组i个子段和的最大值
int *c=new int[n+1];//存储上一个子段,即i-1子段和的最大值
b[0]=0;c[1]=0;
for(int i=1;i<=m;i++)
{
b[i]=b[i-1]+a[j];//a[j]单独作为一项
c[i-1]=b[i];
int max=b[i];
for(int j=i+1;j<=i+n-m;j++)
{
//共有m个子段,现在用了i段,假设一个元素占一段,现在最多剩下(n-(m-i))个元素
b[j]=b[j-1]>c[j-1]?b[j-1]+a[j]:c[j-1]+a[j];
//比较第j-1个子段和与第j-2个子段和,用大的那个加上a[j]得到第j个子段和
c[j-1]=max;//更新第i-1个子段和的最大值
}
c[i+n-m]=max;
}
int sum=0;
for(int i=m;i<=n;i++)
{
if(sum<b[i])
sum=b[i];//更新最大m子段和
}
return sum;
}**
例3:凸多边形最优三角划分
template <class Type>
void MinWeightTrianhulation(int n,Type **t,int **s)
{
//n条边,t为最优三角剖分权函数值,s[i][j]记录与与v[i-1]
//和v[j]一起构成三角形的第3个顶点的位置,用其中三角形把
//多边形分成左右两半,求出左右2个子问题的最优解,
//再加上该三角形,最后的权函数值就是问题的解
for(int i=1;i<=n;i++)t[i][i]=0;//退化的2顶点多边形权值为0
for(int r=2;r<=n;r++)//子问题规模
for(int i=1;i<=n-r+1;i++){
//确定每个子问题的开始的地方
int j=i+r-1;//每个子问题最后的地方
t[i][j]=t[i+1][j]+w(i-1,i,j);//从第i个三角形隔开,把问题分成2个子问题,算出三角形v[i-1][i][j]的权函数,加上子多边形i+1-j的最优三角剖分的最优u权值
s[i][j]=i;//断点在i
for(int k=i+1;k<i+r-1;k++){
//从每个子问题的第二个三角形开始分成2半
int u=t[i][k]+t[k+1][j]+w(i-1,k,j);
if(u<t[i][j]){
t[i][j]=u;s[i][j]=k;}//更新最小权函数和断点
}
}
}
例4:多边形游戏
void MinMax(int n,int i,int s,int j,int &minf,int& maxf)
{
//多边形顶点数为n,把环变成链,s为最后一次合并的边,
//代表一个运算符号,p[i,j]表示的是链的起点i和长度j,
//子问题的最大值和最小值minf,maxf
//记录每个子问题的最大最小值
int e[5];
int a=m[i][s][0],b=m[i][s][1],r=(i+s-1)%n+1,c=m[r][j-s][0],d=m[r][j-s][1];
//a,b是p[i,s]子问题的最大值,最小值,
//c,d是p[i+s,j-s]子问题的最大最小值,
//为了算出正确的偏移量s,使用循环数组的的计算方法,
//因为多边形是一个封闭的环,如果i+s>n,那么需要取模,
//比如i=0,s=3,第二段的起点应该是3,而不是0,
//因为i+s>i,所以r不能用(i+s)%n来计算
if(op[r]=='+'){
minf=a+c;maxf=b+d;}//在第二个子问题的起点
//如果运算符为+求出最小值最大值
else
{
e[1]=a*c;e[2]=a*d;
e[3]=b*c;e[4]=b*d;
minf=e[1];maxf=e[2];
for(int i=2;i<5;i++){
if(minf>e[i])minf=e[i];//求出4个数相乘的最大最小值
if(maxf<e[i])maxf=r[i];}
}
}
int PolyMax(int n)
{
//划分子问题
int minf,maxf;
for(int j=2;j<=n;j++)//迭代链的长度
for(int i=1;i<=n;i++)//迭代起点
for(int s=1;s<j;s++){
//迭代最后一次合并位置
MinMax(n,i,s,j,minf,maxf,m,op)
if(m[i][j][0]>minf)m[i][j][0]=minf;
if(m[i][j][1]>maxf)m[i][j][1]=maxf;
//每个子问题的最大最小值都记录在m数组中
}
int temp=m[1][n][1];
for(int i=2;i<=n;i++)
if(temp<m[i][n][1])temp=m[i][n][1];
return temp;//由子问题计算p[1][n]问题的最大值
}
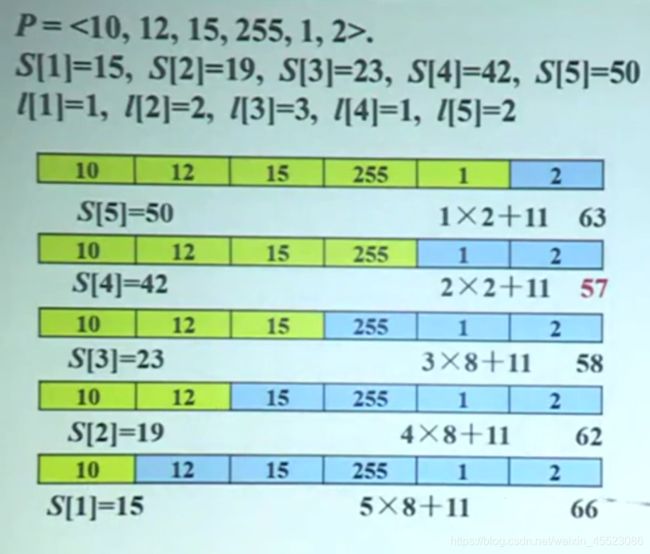
例5:图像压缩
void Compress(int n,int p[],int s[],int l[],int b[])
{
int Lmax=256,header=11;
s[0]=0;
for(int i=1;i<=n;i++){
//子问题后边界
b[i]=length(p[i]);//灰度值的位数
int bmax=b[i];//最后一段只有一个像素,把子问题的最后一个元素当成最后一段
s[i]=s[i-1]+bmax;
l[i]=1;//最后一段的长度是1
for(int j=2;j<=i&&j<=LMax;j++){
//最后一段的长度加长
if(bmax<b[i-j+1])bmax=b[i-j+1];//寻找子问题中最大的灰度值存储位数
if(s[i]>s[i-j]+j*bmax){
//最后一段的位数+去掉最后一段的最优分段的存储位数如果小于之前算出来的存储位数
s[i]=s[i-j+1]+j*bmax;//更新存储位数
l[i]=j;//更新最后一段的长度
}
}
s[i]+=header;//算上端头的开销11
}
}
int length(int i)
{
int k=1;i=i/2;
while(i>0){
k++;i=i/2;}
return k;
}
例5:电路布线
void MNS(int C[],int n,int **size)
{
//C代表一个子问题的子集,pi(i)
for(int j=0;j<C[1];j++)size[1][j]=0;
//i=1,j
for(int j=C[1];j<=n;j++)size[1][j]=1;
//i=1,j>pi(1),导线条数为1
for(int i=2;i<n;i++){
//i>=2
for(int j=0;j<C[i];j++)size[i][j]=size[i-1][j];
//j
for(int j=C[i];j<=n;j++)
//j>pi(i),比较选取和不选取第i条导线的最优解
size[i][j]=max(size[i-1][j],size[i-1][C[i]-1]+1);
}
size[n][n]=max(size[n-1][n],size[n-1][C[n]-1]+1];
}
构造最优解
void Traceback(int C[],int **size,int n,int Net[],int& m)
{
//Net[]存储MNS(n,n)中的m条连线
int j=n;
m=0;
for(int i=n;i>1;i--)//从后往前寻找连线条数
if(size[i][j]!=size[i-1][j]){
Net[m++]=i;j=C[i]-1;}
//不选取第i条导线
if(i>C[1])Net[m++]=1;//看第一条线要不要
}