常见快速搜索算法图解

搜索

搜索是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的，因为该项目是否存在。搜索的几种常见方法：顺序查找、二分法查找、二叉树查找、哈希查找

二分查找

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

二分查找的实现

(非递归实现)

def binary_search_2(alist,item):
    """二分查找：while版"""
    n = len(alist)
    first = 0
    last = n -1
    while first <= last:
        mid = (first+last) // 2
        if alist[mid] == item:
            return True
        elif item < alist[mid]:
            last = mid - 1
        else:
            first = mid + 1
    return False

(递归实现)

def binary_search(alist,item):
    """二分查找：递归版"""
    n = len(alist)
    if n > 0:
        mid = n // 2
        if alist[mid] == item:
            return True
        elif item<alist[mid]:
            return binary_search(alist[:mid],item)
        else:
            return binary_search(alist[mid+1:],item)
    return False

时间复杂度

• 最优时间复杂度：$O（1）$
• 最坏时间复杂度：$O（lo{g}_{2}n）$

哈希查找

散列表也叫作哈希表（hash table），这种数据结构提供了键（Key）和值（Value）的映射关系。只要给出一个Key，就可以高效查找到它所匹配的Value，时间复杂度接近于$O(1)$。

散列表是如何根据Key来快速找到它所匹配的Value呢？

哈希函数

散列表在本质上也是一个数组。可是数组只能根据下标，像a[0]、a[1]、a[2]、a[3]、a[4]这样来访问，而散列表的Key则是以字符串类型为主的。

例如以学生的学号作为Key，输入002123，查询到李四；或者以单词为Key，输入by，查询到数字46……

所以我们需要一个“中转站”，通过某种方式，把Key和数组下标进行转换。这个中转站就叫作哈希函数。

这个所谓的哈希函数是怎么实现的呢？在不同的语言中，哈希函数的实现方式是不一样的。这里以python的字典（dictionary）为例，来看一看哈希函数在python中的实现。

在python及大多数面向对象的语言中，每一个对象都有属于自己的hashcode，这个hashcode是区分不同对象的重要标识。无论对象自身的类型是什么，它们的hashcode都是一个整型变量。既然都是整型变量，想要转化成数组的下标也就不难实现了。最简单的转化方式是什么呢？是按照数组长度进行取模运算。

index = HashCode (Key) % Array.length

通过哈希函数，我们可以把字符串或其他类型的Key，转化成数组的下标index。

如给出一个长度为8的数组，则当key=001121时，

index = HashCode ("001121") % Array.length = 1420036703 % 8 = 7 而当key=this时， index = HashCode ("this") % Array.length = 3559070 % 8 = 6

字典的读写操作

有了哈希函数，就可以在字典中进行读写操作了。

1.写操作

写操作就是在散列表中插入新的键值对（在python中用dict）。如调用dict= {‘002931’: ‘王五’}，意思是插入Key为002931、Value为王五的键值对。具体该怎么做呢？

第1步，通过哈希函数，把Key转化成数组下标5。
第2步，如果数组下标5对应的位置没有元素，就把这个dict填充到数组下标5的位置。

但是，由于数组的长度是有限的，当插入的dict越来越多时，不同的Key通过哈希函数获得的下标有可能是相同的。例如002936这个Key对应的数组下标是2；002947这个Key对应的数组下标也是2。

这种情况，就叫作哈希冲突。

哈希冲突是无法避免的，既然不能避免，我们就要想办法来解决。解决哈希冲突的方法主要有两种，一种是开放寻址法，一种是链表法。

开放寻址法的原理很简单，当一个Key通过哈希函数获得对应的数组下标已被占用时，我们可以“另谋高就”，寻找下一个空档位置。
以上面的情况为例，dict6通过哈希函数得到下标2，该下标在数组中已经有了其他元素，那么就向后移动1位，看看数组下标3的位置是否有空。

很不巧，下标3也已经被占用，那么就再向后移动1位，看看数组下标4的位置是否有空。

幸运的是，数组下标4的位置还没有被占用，因此把Entry6存入数组下标4的位置。

这就是开放寻址法的基本思路。当然，在遇到哈希冲突时，寻址方式有很多种，并不一定只是简单地寻找当前元素的后一个元素，这里只是举一个简单的示例而已。

在python中就是采用的开放定址法来解决冲突,开放定址法也称为闭散列法.当产生冲突时,python会通过一个二次探测函数f,计算下一个候选索引, 如果索引不可用,就再次用f探测.直到找到一个可用的位置.

之所以叫做闭散列法，就是因为冲突的元素没有开辟额外的存储空间，还是在原先hash表的空间范围之内。

2.读操作
讲完了写操作，我们再来讲一讲读操作。读操作就是通过给定的Key，在散列表中查找对应的Value。

例如调用 dict.get(“002936”)，意思是查找Key为002936的dcit在散列表中所对应的值。

3. 扩容
在讲解数组时，曾经介绍过数组的扩容。既然散列表是基于数组实现的，那么散列表也要涉及扩容的问题。

首先，什么时候需要进行扩容呢？

当经过多次元素插入，散列表达到一定饱和度时，Key映射位置发生冲突的概率会逐渐提高。这样一来，大量元素拥挤在相同的数组下标位置，形成很长的链表，对后续插入操作和查询操作的性能都有很大影响。

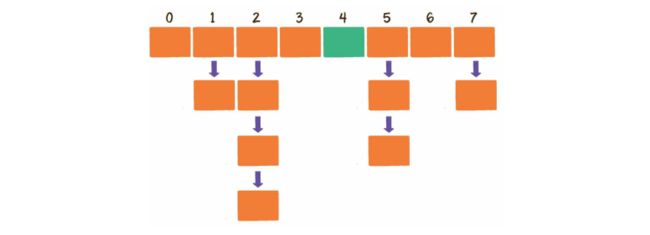
这时，散列表就需要扩展它的长度，也就是进行扩容。

对于python中的散列表实现dict来说，影响其扩容的因素有两个。

• Capacity，即散列表的当前长度
• LoadFactor，即散列表的填装因子，默认值为0.75f

散列表的填装因子很容易计算。

散列表使用数组来存储数据，因此你需要计算数组中被占用的位置数。例如，下述散列表的填装因子为2/5，即0.4。

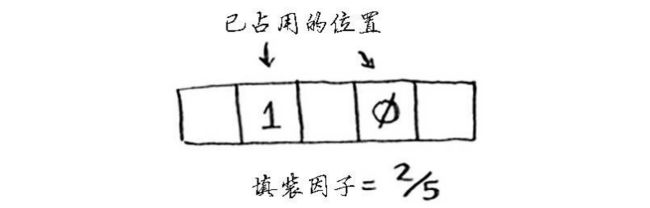
填装因子大于1意味着被占用元素的数量超过了数组的长度。一旦填装因子开始增大，你就需要在散列表中添加位置，这被称为调整长度。

以上就是散列表各种基本操作的原理。由于dict的实现代码相对比较复杂，这里就不直接列出源码了，有兴趣的读者可以在python中直接阅读PyDictObject对象的源码。

二叉树查找

二叉查找树（binary search tree）在二叉树的基础上增加了以下几个条件。

• 如果左子树不为空，则左子树上所有节点的值均小于根节点的值
• 如果右子树不为空，则右子树上所有节点的值均大于根节点的值
• 左、右子树也都是二叉查找树

下图就是一个标准的二叉查找树。

二叉查找树的这些条件有什么用呢？当然是为了查找方便。

例如查找值为4的节点，步骤如下。

1. 访问根节点6，发现4<6。
   
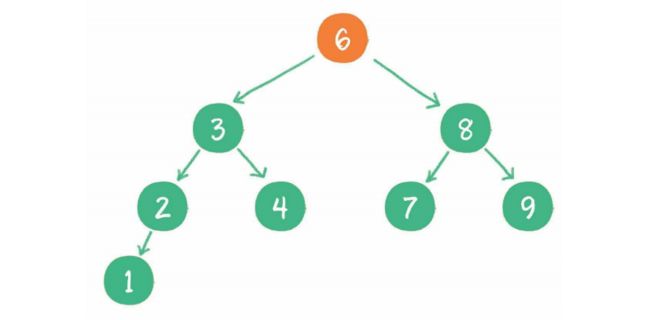
2. 访问节点6的左孩子节点3，发现4>3。
   
3. 访问节点3的右孩子节点4，发现4=4，这正是要查找的节点。
   
   对于一个节点分布相对均衡的二叉查找树来说，如果节点总数是n，那么搜索节点的时间复杂度就是O(logn)，和树的深度是一样的。

这种依靠比较大小来逐步查找的方式，和二分查找算法非常相似。