算法导论 第7章 快速排序 —— 练习还没做,记得补锅
今天来学习第七章——快速排序。
作为占据一章的排序,快速排序可谓是重量级选手。
- 实际排序中最好的选择,因为
- (1) 其平均性能非常好,期望实践复杂度为 O(n lgn);
- (2) 可进行原址排序;
- (3) 在虚拟环境中也能很好地工作。
- 适用于基于随机的数据,因为其最坏情况时间复杂度为 n^{2}。最坏情况即所有元素都一样。
1. 概念
2. 伪代码
QUICKSORT(A, p, r)
if p < r
q = PARTITION(A, p, r)
QUICKSORT(A, p, q - 1)
QUICKSORT(A, q + 1, r)
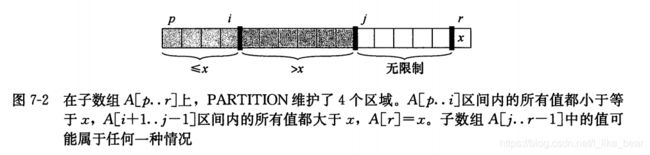
PARTITION(A, p, r)
x = A[r] // pivot element, 主元
i = p - 1
for j = p to r - 1 // 无限制区域元素划分
if A[j] <= x
i = i + 1
exchange A[i] with A[j]
// 循环结束后,修改主元与中间元素。
// 这一步操作使得在主元 A[p] 左边的元素都比主元小,在主元 A[p] 右边的元素都比主元大。
exchange A[i + 1] with A[r]
return i + 1为了排序一整个数组,一开始调用的函数是 QUICKSORT(A, 1, A.length)
3. Java 实现
public class QuickSort {
public static void main(String[] args) {
int len = 10;
int[] a = new int[len];
for (int i = 0; i < len; i++) {
a[i] = (int)(Math.random() * 100);
}
// 排序之前
for (int num: a) {
System.out.print(num + "\t");
}
quickSort(a, 0, len - 1);
// 排序之后
System.out.println();
for (int num: a) {
System.out.print(num + "\t");
}
}
public static void quickSort(int[] a, int p, int r) {
if (p < r) {
int q = partition(a, p, r);
quickSort(a, p, q - 1);
quickSort(a, q + 1, r);
}
}
public static int partition(int[] a, int p, int r) {
int x = a[r]; // 主元
int i = p - 1;
for (int j = p; j < r; j++) {
// 无限制区域
if (a[j] <= x) {
i++;
change(a, i, j);
}
}
change(a, i + 1, r);
return i + 1;
}
public static void change(int[] a, int first, int second) {
int tmp = a[first];
a[first] = a[second];
a[second] = tmp;
}
}
某一次运行结果如下
65 10 95 21 22 72 95 22 32 31
10 21 22 22 31 32 65 72 95 95
4. 复杂度
以下引用来自 算法复杂度分析
实际中,我们一般仅考量算法在最坏情况下的运行情况,也就是对于规模为 n 的任何输入,算法的最长运行时间。这样做的理由是:
(1) 一个算法的最坏情况运行时间是在任何输入下运行时间的一个上界(Upper Bound)。
(2) 对于某些算法,最坏情况出现的较为频繁。
(3) 大体上看,平均情况通常与最坏情况一样差。
渐近记号(Asymptotic Notation)通常有 O、 Θ 和 Ω 记号法。
Θ 记号渐进地给出了一个函数的上界和下界,
当只有渐近上界时使用 O 记号,
当只有渐近下界时使用 Ω 记号。
尽管技术上 Θ 记号较为准确,但通常仍然使用 O 记号表示。
使用 O 记号法(Big O Notation)表示最坏运行情况的上界。例如,
线性复杂度 O(n) 表示每个元素都要被处理一次。
平方复杂度 O(n^2) 表示每个元素都要被处理 n 次。
在算法导论中,采用记号 lg n = log2 n ,也就是以 2 为底的对数。
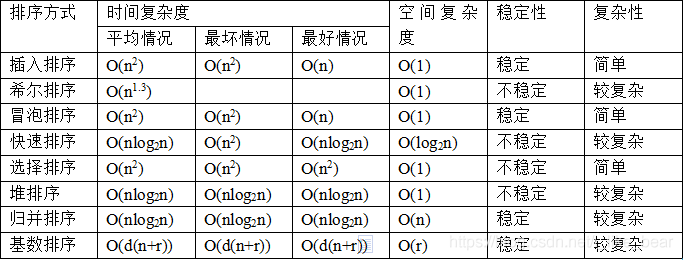
下图源于 各个排序算法的时间复杂度和稳定性,快排的原理
5. 练习题(不想做啊,好难啊
7.1-2 当数组 A[p… r] 中的元素都相同时,PARTTION 返回的 q 值是什么? 修改 PARTITION, 使得当数组 A[p… r] 中所有元素的值都相同时,q=⌊(p+r)/2」。
① 当元素相同时, 返回值 q =i+1=r-1+1=r.
② 修改思路:TODO
7.1-3 请简要地证明:在规模为n的子数组.上,PARTITION的时间复杂度为日(n)。
TODO
7.1-4 如何修改QUICKSORT,使得它能够以非递增序进行排序?
TODO