实用四元数
四元数(Quaternion)相关的介绍材料非常多,这里针对其中几个实用问题进行阐述。
文章目录
- 四元数初步
-
- 四元数运算
- 四元数与刚体旋转
-
- 四元数与轴角对
- 四元数旋转
- 四元数与角速度
- 单位四元数插值
-
- SLERP
- 四元数与黎曼流形
-
- 旋转距离
- 黎曼流形
- 其它参考
四元数初步
相关介绍可参考此文或此文(英文)。
相对于复数的二维空间表示,四元数可理解为一种四维空间表示。四元数是由一个实数和三个元素 i , j , k i,j,k i,j,k组成: q = w + a i + b j + c k q = w + ai + bj + ck q=w+ai+bj+ck 三个元素之间有如下关系: i 2 = j 2 = k 2 = i j k = − 1 i^2 = j^2 = k^2 = ijk = -1 i2=j2=k2=ijk=−1
四元数还可以定义为: q = w + u ⃗ q = w + \vec u q=w+u
四元数运算
四元数虚部的乘法不具有交换律,例如: i j = k , j i = − k ; j k = i , k j = − i ; k i = j , i k = − j ij = k, ji = -k;\quad jk = i, kj = -i;\quad ki = j, ik = -j ij=k,ji=−k;jk=i,kj=−i;ki=j,ik=−j 四元数的共轭定义为: q ∗ = w − a i − b j − c k q^{*}=w-ai-bj-ck q∗=w−ai−bj−ck 四元数的模定义为: ∣ q ∣ = q ⋅ q ∗ = w 2 + a 2 + b 2 + c 2 |q| = \sqrt{q\cdot q^{*}} = \sqrt{w^2+a^2+b^2+c^2} ∣q∣=q⋅q∗=w2+a2+b2+c2 注意 ( q p ) ∗ = p ∗ q ∗ (qp)^{*} = p^{*}q^{*} (qp)∗=p∗q∗,四元数的乘逆为: q − 1 = q ∗ ∣ q ∣ 2 q^{-1}=\frac{q^{*}}{|q|^{2}} q−1=∣q∣2q∗
与复数一样,四元数求和将不同元素加起来即可,满足交换律和结合律。
令: q = w + u ⃗ , p = t + v ⃗ q = w+\vec u,\quad p = t + \vec v q=w+u,p=t+v两个四元数之间的非可交换乘积通常被称为格拉斯曼积,其完整形式为: p q = w t − v ⃗ ⋅ u ⃗ + w v ⃗ + t u ⃗ + v ⃗ × u ⃗ pq = wt-\vec v\cdot\vec u + w\vec v + t\vec u + \vec v \times \vec u pq=wt−v⋅u+wv+tu+v×u 或 p q = ( w t − a x − b y − c z ) + ( a t + w x + b z − c y ) i + ( b t + w y + c x − a z ) j + ( c t + z w + a y − x b ) k \begin{aligned}pq = (wt-ax-by-cz) \\ +(at+wx+bz-cy)i \\ +(bt+wy+cx-az)j \\ +(ct+zw+ay-xb)k\end{aligned} pq=(wt−ax−by−cz)+(at+wx+bz−cy)i+(bt+wy+cx−az)j+(ct+zw+ay−xb)k 由于四元数乘法的不可交换性, p q pq pq并不等于 q p qp qp: q p = w t − u ⃗ ⋅ v ⃗ + w v ⃗ + t u ⃗ − v ⃗ × u ⃗ qp = wt-\vec u\cdot \vec v+w\vec v + t\vec u-\vec v\times \vec u qp=wt−u⋅v+wv+tu−v×u
四元数点积: p ⋅ q p\cdot q p⋅q
点积也叫欧几里得内积,四元数点积等同于一个四维向量的点积。点积是可交换积,返回一个标量: p ⋅ q = w t + u ⃗ ⋅ v ⃗ = w t + a x + b y + c z p\cdot q = wt + \vec u \cdot \vec v = wt+ax+by+cz p⋅q=wt+u⋅v=wt+ax+by+cz
四元数叉积: p × q p\times q p×q
四元数叉积和向量叉积等价,返回一个向量: p × q = p q − q p 2 = u ⃗ × v ⃗ = ( b z − c y ) i + ( c x − a z ) j + ( a y − x b ) k \begin{aligned}p\times q &= \frac{pq-qp}{2} \\ &= \vec u \times \vec v \\ &= (bz-cy)i+(cx-az)j+(ay-xb)k \end{aligned} p×q=2pq−qp=u×v=(bz−cy)i+(cx−az)j+(ay−xb)k 四元数叉积满足结合律、不满足交换律。叉积的模等于模的乘积,这样保证了单位四元数的叉积依然是单位四元数。
四元数逆: p − 1 p^{-1} p−1
四元数的转置通过 p − 1 p = 1 p^{-1}p = 1 p−1p=1 被定义。其构建方式与复倒数相同: p − 1 = p ∗ p ⋅ p p^{-1} = \frac{p^{*}}{p\cdot p} p−1=p⋅pp∗ 一个四元数与自身的点积是一个标量。单位四元数的转置于共轭相同。
四元数的符号: s g n ( p ) \mathrm{sgn}(p) sgn(p)
复数的符号定义为单位圆上一个方向与原复数相同的复数。四元数的符号产生于单位四元数: s g n ( p ) = p ∣ p ∣ \mathrm{sgn}(p) = \frac{p}{|p|} sgn(p)=∣p∣p
四元数的辐角: arg ( p ) \arg(p) arg(p)
辐角函数可找出一个四元数偏离单位标量的角度。此函数输出一个标量角度: arg ( p ) = arccos ( w ∣ p ∣ ) \arg(p) = \arccos\left( \frac{w}{|p|} \right) arg(p)=arccos(∣p∣w)
四元数的幂与对数:
自然幂: exp ( p ) = exp ( w ) ( cos ( ∣ u ⃗ ∣ ) + s g n ( u ⃗ ) sin ( ∣ u ⃗ ∣ ) ) \exp(p) = \exp(w)(\cos(|\vec u|)+\mathrm{sgn}(\vec u)\sin(|\vec u|)) exp(p)=exp(w)(cos(∣u∣)+sgn(u)sin(∣u∣))
自然对数: ln ( p ) = ln ( ∣ p ∣ ) + s g n ( u ⃗ ) arg ( p ) \ln(p) = \ln(|p|)+\mathrm{sgn}(\vec u)\arg(p) ln(p)=ln(∣p∣)+sgn(u)arg(p)
单位四元数的平均值:
此文
F.L. Markley, Y. Cheng, J.L. Crassidis, Y. Oshman, Averaging quaternions, J. Guid. Control Dyn. 30 (4) (2007) 1193–1197.
中介绍,单位四元数可以被看作是单位长度的方向向量,对 4 × 4 4\times 4 4×4矩阵:
C = ∑ n = 1 N q n ⋅ q n T C = \sum_{n=1}^{N}q_{n}\cdot q_{n}^{T} C=n=1∑Nqn⋅qnT 采用主成分分析,找到其最大特征值对应的正则化的特征向量作为其平均值。
四元数与刚体旋转
单位四元数,即绝对值为1的四元数( ∥ q ∥ 2 = v 2 + u 2 = 1 \|q\|^{2} = v^{2}+\mathbf{u}^{2} = 1 ∥q∥2=v2+u2=1),若实部为 cos ( θ ) \cos(\theta) cos(θ),它的共轭作用是一个角度为 2 θ 2\theta 2θ 的转动,旋转轴为虚部的方向。相比于欧拉角,四元数表达式无奇点;相比于SO3矩阵,四元数也更为简洁。两个单位四元数的乘积也是单位四元数,所有四元数的集合组成一个三维球 S 3 \mathcal{S}^3 S3 和在乘法下的一个群(李群)。注意四元数表示的旋转是一个2-1映射,因为 q q q 与 − q -q −q 表达的是同一个旋转。
四元数与轴角对
绕旋转轴 n n n 旋转 θ \theta θ 角(右手法则),表示为四元数:
q = cos ( θ 2 ) + sin ( θ 2 ) ( n x i + n y j + n z k ) q = \cos\left(\frac{\theta}{2}\right) + \sin\left(\frac{\theta}{2}\right)\left( n_{x}i+n_{y}j+n_{z}k \right) q=cos(2θ)+sin(2θ)(nxi+nyj+nzk) 换一种说法:给定轴角对 ( ω , θ ) (\omega, \theta) (ω,θ) 来表示一个绕 ω \omega ω 转 θ \theta θ 的旋转,那么对应的单位四元数被定义为:
q = ( cos θ 2 , sin θ 2 ω ) q = \left( \cos\frac{\theta}{2}, \sin\frac{\theta}{2}\omega \right) q=(cos2θ,sin2θω)
这个网站可以很直观的展示四元数轴角对。注意, q q q 与 − q -q −q 代表的是相同的旋转(Quaternions have a double cover of the rotation manifold)。
四元数旋转
扩展一个欧氏空间中的点到四元数空间,只需要将其定义为 p = ( 0 , x , y , z ) p=(0,x,y,z) p=(0,x,y,z) 即可。执行下述乘法可以使点 p p p 绕 n n n 旋转: p ′ = q p q − 1 p' = qpq^{-1} p′=qpq−1 这个运算被称为哈密尔顿积(Hamilton product)。注意这和使用复数进行2D旋转是不同的。
多次旋转的情况: p ′ = q 2 ( q 1 p q 1 − 1 ) q 2 − 1 = ( q 2 q 1 ) p ( q 1 − 1 q 2 − 1 ) = ( q 2 q 1 ) p ( q 2 q 1 ) − 1 p' = q_{2}(q_{1}pq_{1}^{-1})q_{2}^{-1} = (q_{2}q_{1})p(q_{1}^{-1}q_{2}^{-1}) = (q_{2}q_{1})p(q_{2}q_{1})^{-1} p′=q2(q1pq1−1)q2−1=(q2q1)p(q1−1q2−1)=(q2q1)p(q2q1)−1 注意旋转是从右向左发生的。
四元数与角速度
定义了距离之后,下一步可以定义导数。采用轴角表示,定义角速度 ω ( t ) \omega(t) ω(t),那么四元数的导数 q ˙ \dot{q} q˙ 表示为: q ˙ = 1 2 ω q \dot{q} = \frac{1}{2}\omega q q˙=21ωq 此处角速度 ω \omega ω 可以被看成是一个拥有0标量的四元数。上一节中指数映射可用于求解上述微分方程,或进行积分:
给定当前时刻方向 q ( t ) q(t) q(t) 和当前时刻角速度 ω ( t ) \omega(t) ω(t),那么,在时间段 Δ t \Delta t Δt 内(假设角速度不变): q ( t + Δ t ) = exp ( Δ t 2 ω ) q ( t ) q(t+\Delta t) = \exp\left( \frac{\Delta t}{2}\omega \right)q(t) q(t+Δt)=exp(2Δtω)q(t)
单位四元数插值
如前所述,单位四元数定义在一个单位球面 S 3 \mathcal{S}^{3} S3 上,两个单位四元数 q 1 q_{1} q1 和 q 2 q_{2} q2 之间的插值是通过球面上的一个路径最短的圆弧运动实现的。两者这件的变动(displacement)为 q 1 q 2 ∗ q_{1}q_{2}^{*} q1q2∗ 。
SLERP
球面线性插值(Spherical Linear Interpolation)运算非常有用,因为它可以实现两个四元数间的平滑插值,避免欧拉角插值的角度限制问题、万向锁问题(导致抖动、路径错误,根本问题是插值过程中角速度不恒定)。
理论上,计算四元数插值的步骤如下:
- 计算两个四元数的差,利用逆矩阵推导。
- 计算差的一部分,即四元数求幂。
- 在起始的值上加上差的一部分,使用四元数乘法来组合角位移。
其主要思想是施密特正交。然而实践中,有一种更有效的方法。所有单位四元数都存在于一个4D球面上,结果如下:(假设旋转的角度是 ϕ \phi ϕ)
S L E R P ( q 0 , q 1 , t ) = sin ( ( 1 − t ) ϕ 2 ) sin ϕ 2 q 0 + sin ( t ϕ 2 ) sin ϕ 2 q 1 \mathrm{SLERP}(q_{0},q_{1},t) = \frac{\sin( (1-t)\frac{\phi}{2})}{\sin \frac{\phi}{2}}q_{0} + \frac{\sin( t\frac{\phi}{2})}{\sin \frac{\phi}{2}}q_{1} SLERP(q0,q1,t)=sin2ϕsin((1−t)2ϕ)q0+sin2ϕsin(t2ϕ)q1
两个四元数之间的角度通过内积计算: ϕ = 2 arccos ( n 1 ⋅ n 2 ) \phi = 2\arccos(n_{1}\cdot n_{2}) ϕ=2arccos(n1⋅n2)
SLERP的推导过程如下图所示:
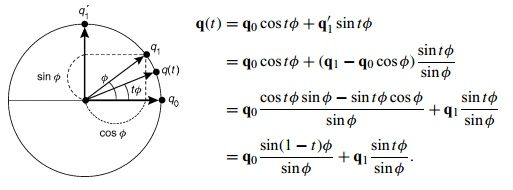
有几点需要注意:
- 四元数 q q q 和 − q -q −q 代表的是相同的方向,但是插值时可能导致不同的结果。解决方法是选择两个数的符号使得它们内积结果非负。
- 如果两个四元数非常接近,那么正弦值非常小,这时除法计算可能会出现问题,解决方法是当正弦非常小时使用线性插值。
由于四元数旋转是乘法形式,上述公式亦可写成: q ( t ) = q 0 ( q 0 − 1 q 1 ) t q(t) = q_{0}(q_{0}^{-1}q_{1})^{t} q(t)=q0(q0−1q1)t
这个表达式可以看作是从起始点逐步”加“与终点的差值的 t t t 倍, 0 < t < 1 0
q 1 = exp ( ln q ) = q q 0 = exp ( 0 ln q ) = exp ( 0 ⋅ n ~ ) = [ cos ( 0 ) , sin ( 0 ) ⋅ n ^ ] = [ 1 , 0 ] \begin{aligned} q^{1} &= \exp(\ln q) = q \\ q^{0} &= \exp(0\ln q) = \exp(0\cdot \tilde{n}) = [\cos(0),\sin(0)\cdot\hat{n}] = [1,0] \end{aligned} q1q0=exp(lnq)=q=exp(0lnq)=exp(0⋅n~)=[cos(0),sin(0)⋅n^]=[1,0] 最后我们令: q 0 = [ 1 , 0 , 0 , 0 ] q_{0} = [1,0,0,0] q0=[1,0,0,0] 以及 q 1 = [ cos θ , sin θ ⋅ n ] q_{1} = [\cos\theta,\sin\theta\cdot n] q1=[cosθ,sinθ⋅n],重新代入SLERP插值公式:
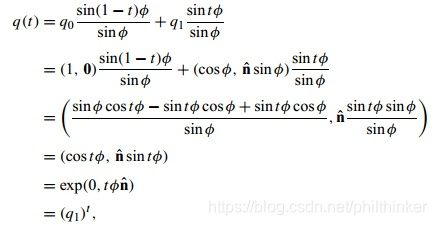
可见两种表现形式可以相互转化。
四元数与黎曼流形
旋转距离
通过距离度量: d ( q 1 , q 2 ) = ∣ q 1 − q 2 ∣ d(q_{1},q_{2}) = |q_{1}-q_{2}| d(q1,q2)=∣q1−q2∣ 四元数可同胚于 R 4 \mathbb{R}^{4} R4的度量空间。衡量两个单位四元数的距离有其它方式,如上一节在探讨SLERP时的视角。
此文中使用内积定义两个四元数的夹角作为距离: θ = arccos ( 2 ( q 1 ⋅ q 2 ) 2 − 1 ) d ( q 1 , q 2 ) = 1 − ( q 1 ⋅ q 2 ) 2 = 1 − cos θ 2 \begin{aligned} \theta &= \arccos\left( 2(q_{1}\cdot q_{2})^{2}-1 \right) \\ d(q_{1},q_{2}) &= 1-(q_{1}\cdot q_{2})^{2} = \frac{1-\cos\theta}{2} \end{aligned} θd(q1,q2)=arccos(2(q1⋅q2)2−1)=1−(q1⋅q2)2=21−cosθ 该度量对于相同方向始终输出 0 0 0 ,对于相差 π \pi π 输出 1 1 1。该定义也被称为测地线(geodesic)距离。注意,这个角度 θ \theta θ 衡量的是这两个四元数 q 1 q_{1} q1、 q 2 q_{2} q2 差别有多大,并非这两个旋转的角度差。
此文中也提到一种类似方法:令 r = q 1 − 1 q 2 r=q_{1}^{-1}q_{2} r=q1−1q2 ,此时 q 1 q_{1} q1 与 q 2 q_{2} q2 的距离等同于 r r r 与 1 + [ 0 , 0 , 0 ] T 1+[0,0,0]^{T} 1+[0,0,0]T 的距离,如果 r r r 实部 r w r_{w} rw 小于零,那么取 r = − r r=-r r=−r。那么对于单位四元数,此时 d ( q 1 , q 2 ) = ϕ = 2 arccos ( r w ) d(q_{1},q_{2})=\phi = 2\arccos(r_{w}) d(q1,q2)=ϕ=2arccos(rw)。与之类似的,在此书中:
Morais, João Pedro, Svetlin Georgiev, and Wolfgang Sprößig. Real quaternionic calculus handbook. Springer Basel, 2014.
作者提到一种利用四元数的对数表示两个四元数之间差异的方法。如前所示,四元数的对数可以写成: log ( q ) = log ( v + u ) = { arccos ( v ) u ∥ u ∥ , u ≠ 0 [ 0 , 0 , 0 ] T , otherwise \log(q) = \log(v+u)=\left\{ \begin{aligned} &\arccos(v)\frac{u}{\|u\|}, u \neq 0 \\ &[0,0,0]^{T}, \text{ otherwise} \end{aligned} \right. log(q)=log(v+u)=⎩⎨⎧arccos(v)∥u∥u,u=0[0,0,0]T, otherwise 注意四元数的对数定义在3维欧式空间内(旋转的轴角表示)。那么, d ( q 1 , q 2 ) = { 2 π , q 2 q 1 ∗ = − 1 + [ 0 , 0 , 0 ] T 2 ∥ log ( q 2 q 1 ∗ ) ∥ , otherwise d(q_{1},q_{2}) = \left\{ \begin{aligned} &2\pi,\quad q_{2}q_{1}^{*} = -1+[0,0,0]^{T} \\ &2\| \log(q_{2}q_{1}^{*}) \|,\quad \text{ otherwise} \end{aligned} \right. d(q1,q2)={ 2π,q2q1∗=−1+[0,0,0]T2∥log(q2q1∗)∥, otherwise 注意上述所有积运算均为乘积运算。如果我们把定义域限制到 S 3 / { − 1 + [ 0 , 0 , 0 ] T } S^{3}/\{-1+[0,0,0]^{T}\} S3/{ −1+[0,0,0]T} 内,那么对数运算是内射(injective)映射。其逆映射,即指数(幂)映射( R 3 → S 3 \mathbb{R}^{3}\to S^{3} R3→S3)如前所述可定义为: exp ( r ) = { cos ( ∥ r ∥ ) + sin ( ∥ r ∥ ) r ∥ r ∥ , r ≠ 0 0 , otherwise \exp(r) = \left\{ \begin{aligned} &\cos(\|r\|)+\sin(\|r\|)\frac{r}{\|r\|},\quad r \neq 0 \\ &0,\quad \text{ otherwise} \end{aligned} \right. exp(r)=⎩⎨⎧cos(∥r∥)+sin(∥r∥)∥r∥r,r=00, otherwise
同样的,如果我们限制两个域为 ∥ r ∥ < π \|r\| < \pi ∥r∥<π 且 S 3 / { − 1 + [ 0 , 0 , 0 ] T } S^{3}/\{-1+[0,0,0]^{T}\} S3/{ −1+[0,0,0]T},那么指数与对数映射变成 one-to-one,连续可微映射,且互为逆映射。
黎曼流形
其它参考
探讨四元数变换与距离的相关帖子:
- Angular Distance Between Quaternions
- Quaternion Exponential Map - Lie group vs. Riemannian Manifold
- 关于李群
- Error measure between two rotations when one matrix might not be a valid rotation
- Comparing two rotation matrices
- 知乎专栏
- 四元数——基本概念
- 四元数——旋转
- 四元数应用——转矩阵、Slerp插值与万向节
- 四元数应用——顺序无关的旋转混合