利用线性同余产生伪随机数+可变参数使用

一、利用线性同余产生伪随机数：

（1）程序设计原理：

线性同余方法（LCG）是个产生伪随机数的方法。

它是根据递归公式：

 

其中 是产生器设定的常数。

LCG的周期最大为 =pow（2,31）-1，但大部分情况都会少于M。要令LCG达到最大周期，应符合以下条件：

一般选取方法：乘数A满足A=4p+1；增量B满足B=2q+1。其中p，q为正整数。

M值得话最好是选择大的，因为M值直接影响伪随机数序列的周期长短。A和B的值越大，产生的伪随机数越均匀

A和M如果互质，产生随机数效果比不互质好。

 

（2）源代码：

package homework2;

 

public class Random {

        

         public static void main(String[] args) {

                   // TODO Auto-generated method stub

                   final int N=1001;

                   double []ran=new double[N];

        double a=Math.pow(7, 5),c=0;

        double m=Math.pow(2,31)-1;

                   ran[0]=1;

                   System.out.println("产生的随机数为：");

                   for(int i=1;i<=1000;++i){

                            ran[i]=(ran[i-1]*a+c)%m;

                            System.out.print((int)ran[i]+" ");

                            if(i%10==0) {

                                     System.out.println("");

                            }

                            if(i%100==0) {

                                     System.out.println("");

                            }

                           

                   }

 

         }

 

}

（3）结果截图：

 

 

（4）附带数学知识：

①原根定义：

设m是正整数，a是整数，若a模m的阶等于φ(m)，则称a为模m的一个原根。（其中φ(m)表示m的欧拉函数）。

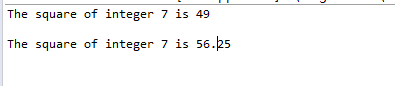
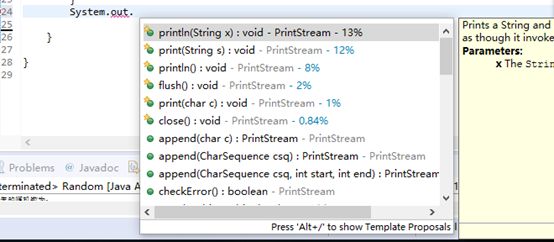
假设一个数g对于P来说是原根，那么g^i mod P的结果两两不同，且有 1

求原根目前的做法只能是从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立，而由于原根一般都不大，所以可以暴力得到。

②欧拉函数性质：

通式：

 

 

其中p1, p2……pn为x的所有质因数，x是不为0的整数。

φ(1)=1（唯一和1互质的数(小于等于1)就是1本身）。

注意：每种质因数只一个。 比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4

若n是质数p的k次幂， 。

因为除了p的倍数外，其他数都跟n互质。

设n为正整数，以 φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值。

φ：N→N，n→φ(n)称为欧拉函数。

欧拉函数是积性函数——若m,n互质， 。

特殊性质：

当n为奇数时，，证明与上述类似。

若n为质数，则。

 

二、可变参数使用：

（1）程序设计原理：

通过设置不同参数类型的同名函数，方便用户的输入，比如此题设置int和double的 square（）函数，就不用在输入时选择参数类型。完善程序。

（2）源代码：

package homework2;

 

public class handAndHead {

 

    public static void main(String[] args) {

        // TODO Auto-generated method stub

 

        System.out.println("The square of integer 7 is "+square(7));

        System.out.println("\nThe square of integer 7 is "+square(7.5));

    }

    public static int square(int x) {

        return x*x;

    }

    public static double square(double y) {

        return y*y;

    }

   

 

}

 

（3）程序结果截图：

 

（4）总结：

通过定义同名函数的不同参数类型，方便调用，提高程序运行效率。

三、查看一下JDK中System.out.println()方法

（1）截图：

 

 

（2）发现：

类似题二的可变参数，可以定义多个不同参数类型的同名函数，这样方便用户进行输入，提高程序的友好性。

转载于:https://www.cnblogs.com/somedayLi/p/7664301.html