震惊!居然还有人不懂二叉树!99%的程序员都会了,不会就点进来吧!
什么!你居然点进来了!看来你就是那百分之一的程序员吧。既然不懂什么是二叉树,那我就来给你讲讲。

1. 树
所谓二叉树,本质上还是个树呀,想要知道什么是二叉树,就要了解树是什么样子的。纳尼!树是什么样子我怎么可能不懂,不就是一根杆子吗!那你就真笨的像个杆子了。

上面这个奇妙形状的物体就是树!(我屮艸芔茻这是树)
那有没有发现树的特点呢,树由树干,树枝组成,一条树干左右分布着很多的树枝,这就是自然界的树。那么二叉树既然也是树,也摆脱不了自然界树的结构。
计算机中的树是一种抽象数据类型(ADT),用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
看得懂吗呆呆,通俗来说,计算机中的树就是自然界中的树倒过来,鲁智深倒拔垂杨柳知道吧,就是他创造了计算机中的树(滑稽)
什么你还看不懂,你比呆呆还呆呆吗!看不懂我就给你画张图
这张图生动形象了吧。
但是这只是自然界中的树的形状,那计算机的树长什么样子呢?
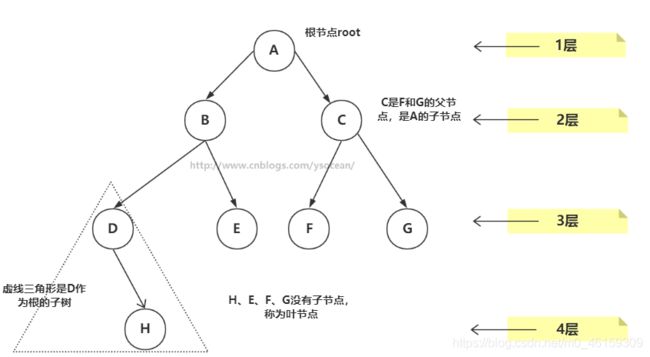
(请不要吐槽画工)
①、节点:上图的圆圈,比如A,B,C等都是表示节点。节点一般代表一些实体,在java面向对象编程中,节点一般代表对象。
②、边:连接节点的线称为边,边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。在Java当中通常表示引用。
树有很多种,向上面的一个节点有多余两个的子节点的树,称为多路树,而每个节点最多只能有两个子节点的一种形式称为二叉树,这也是我们讲解的重点。
2.树的常用术语
①、路径:顺着节点的边从一个节点走到另一个节点,所经过的节点的顺序排列就称为“路径”。
举个栗子:从A到H的路径路过A,B,D,H四个节点。这就被称为一个路径
②、根:树顶端的节点称为根。一棵树只有一个根。
③、父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;B是D的父节点。
简单的来说,就是一个树枝上又分叉了两根树枝,那么这个树枝就是那两个树枝的父亲。
④、子节点:一个节点含有的子树的根节点称为该节点的子节点;D是B的子节点。
⑤、兄弟节点:具有相同父节点的节点互称为兄弟节点;比如上图的D和E就互称为兄弟节点。
⑥、叶节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的H、E、F、G都是叶子节点。
意思就是,一个树枝没有分叉,那就长叶子了,长了叶子的树枝就是叶子树枝,也就是叶子节点
⑦、子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
听说过柳树吗,随便拔个树枝插土里都能生根长成树。子树就是柳树的树枝又生的树。
⑧、节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推。
⑨、深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
通俗易懂的说就是树的任意一个树枝到地面的高度
⑩、高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
3.二叉树的结构
二叉树也是树,自然和树的结构大同小异,光从名字来说,二叉树就是一个树枝分两个叉的树。所以说二叉树就是一个节点只能有两个子节点的树。现在应该都知道二叉树是什么了,那二叉树是怎么工作的呢?它查找一个节点,插入一个新节点,以及删除一个节点,遍历树等工作效率如何,下面我们来一一介绍。
既然是二叉树,那肯定要分左边的树枝和右边的树枝咯,那我给他写两个树枝。
private String rightNode;//右边的树枝
private String leftNode;//左边的树枝
那么树枝有了,这个树要做到,查找,插入的方法我们也要给他写出来
public Tree {
/*
*key:节点参数
*/
//查找节点
public String find(Object key);
//插入新节点
public boolean insert(Object key);
4.二叉树排序
所谓排序就是一个值按一定顺序排列,那二叉树排序的方法又是什么呢?
这边有七个数,分别是3,5,2,6,4,1,7。那么按照我们正常从大到小排序,那就是1,2,3,4,5,6,7。但是在我们二叉树中,得有一个根节点,那么我们把这个数组第一个数当成根,所以根就是3,比根小的数,就放在根的左边,比根大的数就放在根的右边。那么我们继续向下排序,第二个数是5,比3大 那就放在了根的右边,接下来看2比3小,那就放在3的左边,以此类推。最后的结果看下图:

这时候我们来巩固一下刚刚我们讲的几个知识点,这个二叉树的根就是3,父节点有3,2,5,6。叶节点那就是1,4,7。
现在来看看怎么用Java代码来实现这个过程。
import java.util.List;
import java.util.ArrayList;
public class NodeDemo {
public static void main(String args[]){
//定义一堆数字
int[] numbers = {
6,5,8,2,6,6,9};
//声明并实例化Node对象
Node roots = new Node();
//用foreach的方式把numbers的每一个值都以add方法添加到二叉树的节点上
for(int number : numbers){
roots.add(number); //调用添加方法
}
//输出二叉树每一个节点上的值
System.out.println(roots.values());
}
}
class Node {
private Node leftNode; //定义一个左节点
private Node rightNode; //定义一个右节点
private Object value; //定义节点当前值
//定义二叉树的add方法,其添加方式按上面所说添加,形参value是从numbers数组传递过来的值
public void add(Object value){
//判断当前节点是否有值,如果没有则把numbers传过来的值赋给当前节点
if(this.value == null){
this.value = value;
}else{
//如果传过来的值小于或等于当前节点的值则实例化一个Node对象给改节点的左节点,并且左节点调用add方法
if((Integer)value <= (Integer)this.value){
if(this.leftNode == null){
this.leftNode = new Node();
}
this.leftNode.add(value);
}else{
//如果传过来的值大于当前节点的值则实例化一个Node对象给改节点的右节点,并且右节点调用add方法
if(this.rightNode == null){
this.rightNode = new Node();
}
this.rightNode.add(value);
}
}
}
4.查找节点匹配值
- 首先给出一个值A,A会先和根比较大小。
- 比根大的就和右边的子节点比。
- 比根小就和左边的子节点比
- 找到匹配值则返回true,没有则返回flas
下面看代码
//查找节点
//对照上面的main方法
public boolean find(int key) {
private int findnumber = 10;
while(key != null){
if(findnumber > key){
//当前值比查找值大,搜索左子树
findnumber = key.leftNode;
}else if(findnumber < key){
//当前值比查找值小,搜索右子树
findnumber = key.rightNode;
}else{
return findnumber;
}
}
return null;//遍历完整个树没找到,返回null
}
5.遍历二叉树
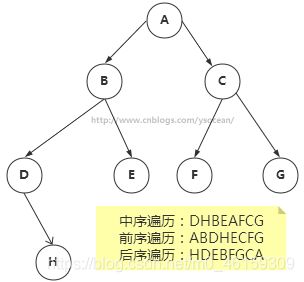
遍历树是根据一种特定的顺序访问树的每一个节点。比较常用的有前序遍历,中序遍历和后序遍历。而二叉搜索树最常用的是中序遍历。
①、中序遍历:左子树——》根节点——》右子树
②、前序遍历:根节点——》左子树——》右子树
//中序遍历
public void infixOrder(Node current){
if(current != null){
infixOrder(current.leftChild);
System.out.print(current.data+" ");
infixOrder(current.rightChild);
}
}
//前序遍历
public void preOrder(Node current){
if(current != null){
System.out.print(current.data+" ");
preOrder(current.leftChild);
preOrder(current.rightChild);
}
}
//后序遍历
public void postOrder(Node current){
if(current != null){
postOrder(current.leftChild);
postOrder(current.rightChild);
System.out.print(current.data+" ");
}
}
6.为什么要用二叉树
对于一般的二叉搜索树(Binary Search Tree),其期望高度(即为一棵平衡树时)为log2n,其各操作的时间复杂度(O(log2n))同时也由此而决定。但是,在某些极端的情况下(如在插入的序列是有序的时),二叉搜索树将退化成近似链或链,此时,其操作的时间复杂度将退化成线性的,即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况,但是在进行了多次的操作之后,由于在删除时,我们总是选择将待删除节点的后继代替它本身,这样就会造成总是右边的节点数目减少,以至于树向左偏沉。这同时也会造成树的平衡性受到破坏,提高它的操作的时间复杂度。
查询速度和二叉树的高度有关,高度越高,查询越慢,成反比关系,当二叉树是有序节点,就会退化为一条链表结构,那么查询一个数据,就要去遍历链表,那么效率大大降低,所有也就有了平衡二叉树。