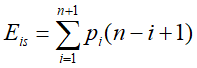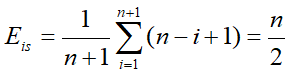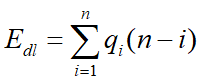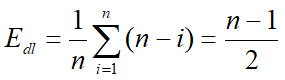数据结构&算法学习笔记——线性表
目录
线性表的类型定义
线性表(Linear_List)定义
线性表操作
线性表的ADT定义
线性表的应用
线性表的顺序表示和实现
线性表的顺序存储结构的表示
线性表的顺序存储结构实现
初始化和销毁
插入元素
插入算法分析
删除元素
删除算法分析
在顺序存储结构下实现“有序表的合并”
线性表优缺点分析
优点
缺点
线性表的链式表示和实现
线性表的链式存储结构的由来
线性表的链式存储结构的定义
单链表的结构的表示
单链表的操作的实现
初始化操作
获取单链表中指定位置的元素
插入操作
删除操作
建表操作
两个有序表的合并操作
循环链表
双向链表
线性表的应用
一元多项式的表示和相加
线性表的类型定义
-
线性表(Linear_List)定义
定义1:线性表是n(n≥0)个相同类型数据元素构成的有限序列,其中n为线性表的长度
定义2:含有n个数据元素的线性表是一个数据结构
Linear_list =(D,R),其中D={ai|ai ∈ ElemSet,i=1,2,…,n,n>=0}
R={N},N={<ai -1,ai >| ai -1,ai ∈ D,i=1,2,…,n}
说明:
1、n定义为表的长度,当n=0时,是一个空表
2、在非空的线性表中,记为( a1,a2 , …, ai -1,ai )有且仅有一个开始结点a1和一个终端结点an。其余的内部结点ai(2≦i≦n-1)都有且仅有一个直接前趋a i-1和一个直接后继ai+1
-
线性表操作
InitList(&L) 初始化,设定一个空表
DestroyList(&L) 删除表操作
ClearList(&L) 表置空操作
ListEmpty(L) 判空操作,若表为空,则返回true,否则返回false
ListLength(L) 求长度函数,返回表的长度
GetElem(L,i,&e) 取元素,返回当前元素
LocateElem(L,e,compare())
PriorElem(L,cur_e,&pre_e) 求前驱函数,返回当前元素的前一个元素
NextElem(L,cur_e,&next_e) 求后继函数,返回当前元素的后一个元素
ListInsert(&L,i,e) 前插操作,在当前元素之前插入一个元素
ListDelete(&L,i,&e) 删除操作,删除指定元素
……
-
线性表的ADT定义
ADT List {
数据对象:D={ ai |ai∈ ElemSet, i=1,2,...,n, n>=0}
数据关系:R1={
基本操作:
InitList(&L)
DestroyList(&L)
ClearList(&L)
ListEmpty(L)
ListLength(L)
GetElem(L,i,&e)
LocateElem(L,e,compare())
PriorElem(L,cur_e,&pre_e)
NextElem(L,cur_e,&next_e)
ListInsert(&L,i,e)
ListDelete(&L,i,&e)
}ADT List
-
线性表的应用
Eg2-1 利用两个线性表LA和LB分别表示两个集合A和B,现要求一个新的集合A=A∪B
void union(List &La,List Lb) {
//将La和Lb的长度分别保存至La_len和Lb_len中
La_len=listlength(La);
Lb_len=listlength(Lb);
//从Lb第一个元素开始, 对Lb的每个元素重复下列操作:
//获取Lb中当前元素,并在La中查找;如果不存在, 将其插在La的尾部
for(i=1;i<=Lb_ben;i++) {
getelem(lb,i,e);
if(!locateelem(la,e,equal))
listinsert(la,++la-en,e)
}
}Eg2-2 已知线性表LA和线性表LB中的数据元素按值非递减有序排列,现要求将LA和LB归并为一个新的线性表LC,且LC中的元素仍按值非递减有序排列
void mergelist(list la,list lb,list &lc)
initlist(lc);
int i=j=1;
int k=0;
la_len=listlength(la);
lb_len=listlength(lb);
while((i<=la_len)&&(j<=lb_len)){
getelem(la, i, ai);
getelem(lb, j, bj);
if(ai<=bj) { listinsert(lc,++k,ai); ++i; }
else{ listinsert(lc,++k,bj); ++j; } }
//将没有处理完的那个线性表的剩余数据元素依次插入到Lc尾部
while(i<=la_len){
getelem((la,i++,ai);
listinsert(lc,++k,ai); }
while(j<=lb_len){
getelem((lb,j++,bj);
listinsert(lc,++k,bi); }
}
线性表的顺序表示和实现
-
线性表的顺序存储结构的表示
定义:用一组地址连续的存储单元依次存储线性表的元素
template
class SqList
{
private:
T *elem;//保持不变,NULL不存在栈
int length;//实际存放元素的个数
int listsize;//可以容纳的最大元素的个数
public:
SqList();
~SqList();
void InputList_Sq();
void OutputList_Sq();
Status ListInsert_Sq(int i, T e);
Status ListDelete_Sq(int i, T &e);
int LocateElem_Sq(T e, Status(*compare)(T, T));
}; Eg2-3 如下线性表如果采用顺序存储
(0,1,2,3,4,5,6,7,8,9)
可以推导出每个元素在内存中的存储地址遵循这样的关系:
Loc(i)=Loc(0)+(i-0) (i=0,1,…,9 )
Eg2-4 如下线性表采用顺序存储方式
| 学号 |
姓名 |
性别 |
年龄 |
成 绩 |
|||
| 高数 |
英语 |
物理 |
体育 |
||||
| 98011 |
张娟 |
女 |
20 |
80 |
86 |
81 |
90 |
| 98012 |
赵军 |
男 |
19 |
82 |
72 |
89 |
86 |
| … |
… |
… |
… |
… |
… |
… |
… |
假设每一数据元素记为ai ,则每个ai占用空间为8,可以推导出每个元素在内存中的存储地址遵循这样的关系:
Loc(ai )=Loc(a1)+(i-1)*8
总结:
假设线性表为(a1,a2 , …, ai -1,ai , …, an ),每个元素ai所占的存储空间为L,则线性表的第i个元素ai的存储位置为:
Loc(ai)=Loc(a1)+(i-1)*L
特点:
1、逻辑顺序与物理顺序一致
2、属随机存取的存储结构,即存取每个元素所花时间相等
-
线性表的顺序存储结构实现
-
初始化和销毁
template
SqList::SqList() {
elem = new T[ListSize];
length = 0;
listsize = ListSize;
}
template
SqList::~SqList() {
delete[] elem;
}
-
插入元素
template
Status SqList::ListInsert_Sq(int i, T e) {
//在数组L的第i个元素之前插入新的元素e
//i的合法值为1<=i<=ListLength_Sq(L)+1
T *p;
if (i<1 || i>L.length + 1)return ERROR;
if (L.length >= L.listsize)
{ //容量已满,增加容量
T *newbase = new T[ListSize + listIncrease];
if (!newbase)return ERROR;
elem = newbase;
listsize += ListIncrease;
}
T *q = &(elem[i - 1]);//新节点的插入位置
for (p = &(elem[length - 1]); p >= q; --p)
*(p + 1) = *p;//往后移动
*q = e; //插入e
++L.length;
}
-
插入算法分析
T *q = &(elem[i - 1]);//新节点的插入位置
for (p = &(elem[length - 1]); p >= q; --p)
*(p + 1) = *p;//往后移动
*q = e; //插入e
++L.length;
分析:移动节点的次数不仅依赖于表的长度L.length,还依赖于插入点的位置i.
1、当i=L.length+1,也就是从表的末端加入,则不移动,其复杂度O(1)
2、当i=1时,也就从表头端加入,如果有n个元素,则需要移动n次,其复杂度O(n)
3、算法的平均期望
-
删除元素
template
Status SqList::ListDelete_Sq(int i, T &e) {
//删除数组中第i个元素,并用e返回其值
//i的合法值为1<=i<=ListLength_Sq(L)
T *p, *q;
if (i<1 || i>length)return ERROR;
p = &(elem[i - 1]);
e = *p;
q = elem + length - 1;//表的尾部位置
for (++p; p <= q; p++) *(p - 1) = *p;
--L.length;
return OK;
}
-
删除算法分析
for (++p; p <= q; p++) *(p - 1) = *p;
--L.length;分析:移动节点的次数同样依赖于表的长度L.length,和删除点位置i
1、当i=L.length,也就是删除末端的元素,则不移动,其复杂度O(1)
2、当i=1时,也就删除前端的元素,如果有n个元素,则需要移动n-1次,其复杂度O(n)
3、算法的平均期望
-
在顺序存储结构下实现“有序表的合并”
template
Status SqList::MergeList_Sq(SqList La, SqList Lb) {
//已知顺序线性表La和Lb的元素按值非递减排列
//归并La和Lb得到新的顺序表Lc,Lc的元素也是按值非递减排列
T *pa, *pb, *pc, *pa_last, *pb_last;
pa = La.elem;
pb = Lb.elem;
listsize = Lc.length = La.length + Lb.length;
pc = elem = new T[listsize];
if (!elem)
exit(OVERFLOW); //空间分配失败
pa_last = La.elem + La.length - 1;
pb_last = Lb.elem + Lb.length - 1;
while (pa <= pa_last && pb <= pb_last) { // 归并
if (*pa <= *pb) *pc++ = *pa++;
else *pc++ = *pb++;
}
while (pa <= pa_last) *pc++ = *pa++; // 插入La的剩余元素
while (pb <= pb_last) *pc++ = *pb++; // 插入Lb的剩余元素
} -
线性表优缺点分析
-
优点
具有简单、运算方便等优点,特别是对于小线性表或长度固定的线性表,采用顺序存储结构的优越性更为突出;
-
缺点
1、 顺序存储插入与删除一个元素,必须移动大量的数据元素,以此对大的线性表,特别是在元素的插入和删除很频繁的情况下,采取顺序存储很是不方便,效率低;
2、顺序存储空间容易满,出现上溢,程序访问容易出问题,顺序存储结构下,存储空间不便扩充;
3、顺序存储空间的分配问题,分多了浪费,分少了空间不足上溢。
线性表的链式表示和实现
-
线性表的链式存储结构的由来
线性表顺序结构最大的缺点就是: 插入和删除时需要移动大量的元素,效率低。
解决思路:
1、让当中毎个元素之间都留有一些空位置,这样要插入时, 就不至于移动。
2、所有的元素都不需要考虑相邻位置,哪有空位就存放在哪里。 但是要让每个元素知道它下一个元素的位置,这样,可以在第一个元素时,找到第二个元素的位置;在第二个元素时,再找到第三个元素的位置,从而所有元素可以通过遍历找到。
-
线性表的链式存储结构的定义
定义:用一组任意的存储单元(可能不连续)存储线性表的数据元素
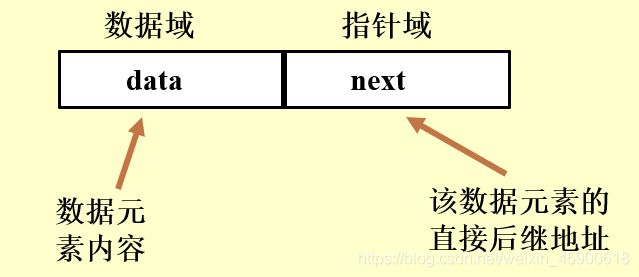
在链式存储结构中,每个存储结点不仅包含数据元素本身的信息(数据),还必须包含各个元素之间逻辑关系的信息,即包含直接后继结点的地址信息(指针域)。
特点:
1、逻辑顺序与物理顺序有可能不一致
2、属顺序存取的存储结构,即存取每个元素必须从第一个元素开始遍历,知道找到需要访问的元素,所以所花的时间不一定相等
-
单链表的结构的表示
template
struct Node
{
T data;
Node *next;
};
template
class LinkedList
{
private:
Node *head;
public:
LinkedList();
~LinkedList();
void CreateList(int n);
Status InputList();
void OutputList();
Status ListInsert(int i, T e);
Status ListDelete(int i, T &e);
Status GetElem_byID(int i, T &e);//已知下标返回值
Status GetElem_byKey(T key,int &i); //已知值返回下标
void MergeList(LinkedList La, LinkedList Lb);
Status Reverse();
}; -
单链表的操作的实现
-
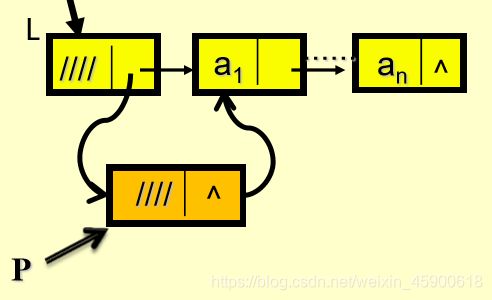
初始化操作
template
LinkedList::LinkedList()
{
head = new Node;
head->next = NULL;
} -
获取单链表中指定位置的元素
template
LinkedList::LinkedList()
{
head = new Node;
head->next = NULL;
}
template
Status LinkedList::GetElem_byID(int i,T &e)
{
Node *p;
p = head->next;
int j = 1; //初始化,p指向第一个结点,j为计数器
while (p && jnext;
++j;
}
if (!p || j > i)return ERROR;//第i个元素不存在
e = p->data; //取第i个元素
return OK;
} -
插入操作
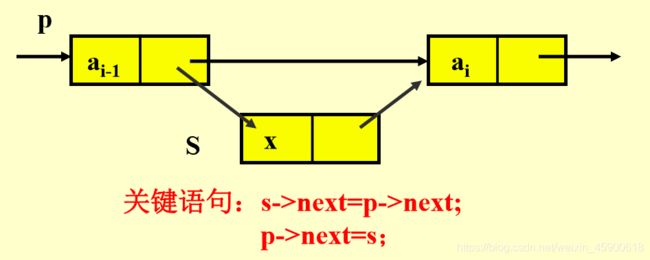
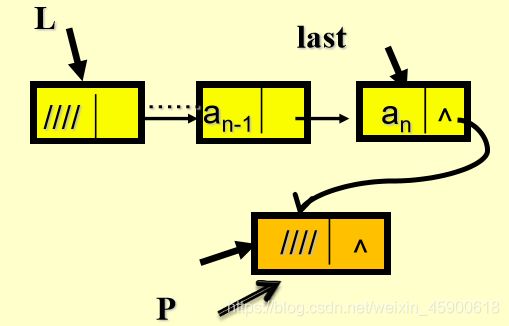
插入运算是将值为x的新结点插入到表的第i个结点的位置上,即插入到ai-1与ai 之间。首先找到ai-1的存储位置p,然后生成一个数据域为x的新结点*s,并令 结点*p的指针域指向新结点,新结点的指针域指向结点ai。从而实现三个结点 ai-1,x和ai之间的逻辑关系的变化,插入过程如图所示:
template
Status LinkedList::ListInsert(int i, T e)
{
Node *p, *s;
p = head;
int j = 0;
while (p&&j < i - 1)
{
p = p->next;
++j;
}
if (!p || j > i - 1)return ERROR;
s = new Node; //生成新结点
s->data = e;
s->next = p->next;
p->next = s;
return OK;
} 设链表的长度为n,合法的插入位置是1≦i≦n+1。注意当i=1时,是头结点,当 i=n+1时,是结点an。算法的时间主要耗费在查找操作上,故时间复杂度亦为O(n)。
-
删除操作
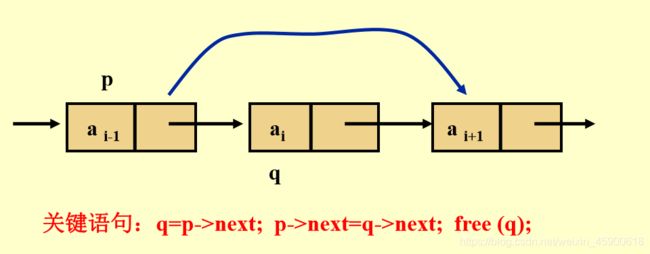
删除运算是将表的第i个结点删去。因为在单链表中结点ai的存储地 址是在其直接前趋结点 a i-1的指针域next中,首先找到a i-1的存储位置p。然后令p–>next指向ai的直接后继结点,即把ai从链上摘下。最后释放结点ai的空间,将其归还给“存储池”。删除过程如图所示:
template
Status LinkedList::ListDelete(int i, T &e)
{
Node *p, *q;
p = head;
int j = 0;
while (p->next&&j < i - 1) //寻找第i个结点,并令p指向其前驱
{
p = p->next;
++j;
}
if (!(p->next) || j > i - 1)return ERROR; //删除位置不合理
q = p->next;
p->next = q->next; //删除并释放结点
e = q->data;
delete q;
return OK;
}
-
建表操作
动态地建立单链表的常用方法有如下两种:
1、逆序建表(头插入法)
从一个空表开始,重复读入数据,生成新结点,将读入数据存放到新结点的数据域中,然后将新结点插入到当前链表的表头上,直到读入结束标志为止。
分析:
创建头结点;
重复下列操作n次:
输入元素信息;
创建结点;
将新结点插入到首端。
//头插法,建立链表:逆位序输入n个元素的值
//建立带表头结点的单链线性表L
template
Status LinkedList::CreateList(int n)
{
Node *p;
for (int i = n; i > 0; i--)
{
p = new Node; //生成新结点
if (!p) return ERROR;
p->data = rand();
p->next = head->next;
head->next = p; //插入到表头
}
return OK;
} 2、正序建表(尾插入法)
头插法建立链表虽算法简单,但生成的链表中结点的次序和输入的顺序相反。若希望二者次序一致,可采用尾插法建表。该方法是将新结点插入到当前链表的表尾上,为此必须增加一个尾指针r,使其始终指向当前链表的尾结点。
分析:
创建头结点;
设置last指针;
重复下列操作n次:
输入元素信息;
创建结点;
将新结点插入到尾端。
//尾插法,建立链表:正位序输入n个元素的值
//建立带表头结点的单链线性表L
template
Status LinkedList::InputList(int n)
{
Node *p, *last;
last = head; //保留last指针
for (int i = 1; i <= n; i++)
{
p = new Node;
if (!p) return ERROR;
p->data = rand();
last->next = p; //插入到表尾
last = p;
}
last->next = NULL;
return OK;
} -
两个有序表的合并操作
template
void LinkedList::MergeList(LinkedList La, LinkedList Lb) {
Node *pa, *pb, *pc, *p;
pa = La.head->next;
pb = Lb.head->next;
pc = head;
while (pa&&pb) {
if (pa->data <= pb->data) {
p = new Node();
p->data = pa->data;
pc->next = p;
pc = pc->next;
pa = pa->next;
}
else {
p = new Node();
p->data = pb->data;
pc->next = p;
pc = pc->next;
pb = pb->next;
}
}
while (pa)
{
p = new Node();
p->data = pa->data;
pc->next = p;
pc = pc->next;
pa = pa->next;
}
while (pb)
{
p = new Node();
p->data = pb->data;
pc->next = p;
pc = pc->next;
pb = pb->next;
}
} -
循环链表
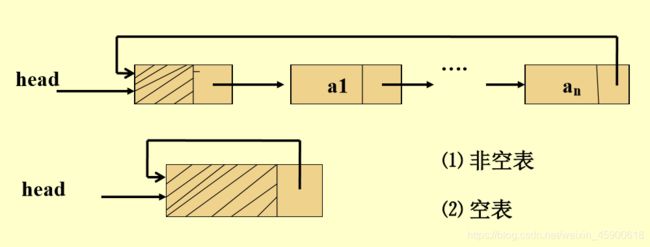
定义:是另外一种形式的链式存储结构。其特点是表中尾结点的指针域指向头结点,形成一个环。从表中任意一点出发都可以找到表中其他的结点。
循环链表的操作和线性链表的操作基本一致,但循环链表中没有NULL指针,故遍历操作时,终止条件不再是判断 p或 p->next是否为空,而是判断它们是否等于某一指定指针,如头指针或尾指针等。
Eg2-5 有一个带头结点的循环单链表L,设计一个算法统计其data域值为x的结点个数。算法描述如下:
int count(LinkList &L, ElemType x)
{
int n = 0;
LinkList p = L->next;
while (p != L) //L是头结点
{
if (p->data == x)
n++;
p = p->next;
}
return n;
}-
双向链表
定义:双向链表是在单链表的每个结点里再增加一个指向其直接前趋的指针域prior。这样就形成的链表中有两个方向不同的链,故称为双向链表。
结构类型定义:
template
struct DulNode
{
T data;
DulNode * prior;
DulNode * next;
};
template
class DulLinkedList
{
private:
DulNode *head;
public:
DulLinkedList();
~DulLinkedList();
Status CreateList(int n); //逆序建表
Status InputList(int n); //正序建表
void OutputList();
Status ListInsert(int i, T e);
Status ListDelete(int i, T &e);
Status GetElem_byID(int i, T &e);//已知下标返回值
Status GetElem_byKey(T key, int &i); //已知值返回下标
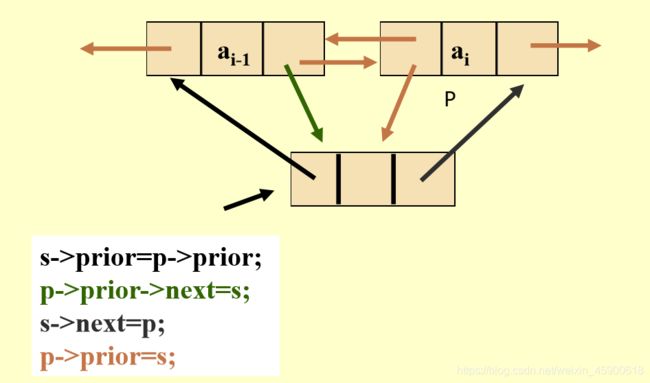
}; 插入操作:
template
Status DulLinkedList::ListInsert(int i, T e)
{
DulNode *p, *s;
p = head;
int j = 0;
while (p&&j < i - 1)//寻找第i-1个结点
{
p = p->next;
++j;
}
if (!p || j > i - 1)return ERROR; //i小于1或者大于表长
s = new DulNode; //生成新结点
s->data = e;
s->next = p->next; //插入L中,在第i-1个元素p之后插入s
p->next->prior = s;
p->next = s;
s->prior = p;
return OK;
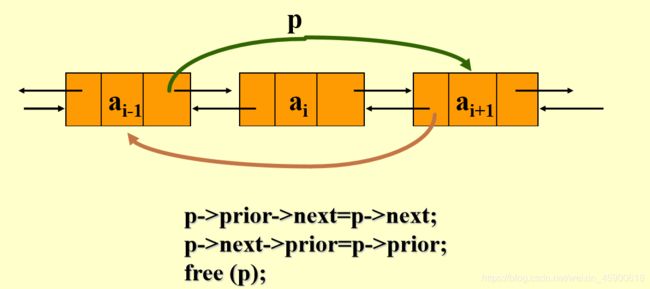
} 删除操作:
template
Status DulLinkedList::ListDelete(int i, T &e)
{
DulNode *p, *q;
p = head;
int j = 0;
while (p->next&&j < i - 1) //寻找第i个结点,并令p指向其前趋
{
p = p->next;
++j;
}
if (!(p->next) || j > i - 1)return ERROR; //删除位置不合理
q = p->next; //保存要删除的结点
p->next = q->next;
q->next->prior = p;
e = q->data;
delete q;
return OK;
} 线性表的应用
-
一元多项式的表示和相加