深度之眼Paper带读笔记GNN.02.LINE

前言

本课程来自深度之眼，部分截图来自课程视频。

文章标题：LINE: Large-scale Information Network Embedding
LINE：大规信息网络特征表示
作者：Jian Tang.etc
单位：MSRA. Microsoft Research Asia
发表会议及时间：WWW 2015
公式输入请参考：在线Latex公式

论文结构

Abstract：介绍背景及提出LINE模型，维护局部和全局网络结构
Introduction：介绍图的重要性、与以前的方法如MDS、ISOMAP、Laplacian eigenmap做对比，强调scalability；DeepWalk缺乏清晰的目标函数
Related Work：传统基于图的MDS、ISOMAP算法；Graph Factorization算法；DeepWalk算法等
Edge Sampling alias sampling：技术，时间复杂度分析，低度点和新点的处理
Model Optimization：模型的优化，负采样技术、SGD算法
LINE算法：1st Proximity、2nd Proximity以及两者的组合
Effectiveness：实验探究模型有效性：baselines选择，参数设定；多类数据集的多个任务：word analogy、document classification、multi-label classification
Experiments：可视化、性能和网络稀疏度、参数实验以及规模性
Discussion：总结提出了一种根据网络结构（一二阶相似度）的目标函数网络表征学习方法，强调了规模性

研究背景

几个缺点：数据稀疏性、高维、没有语义信息
传统的做法是对邻接矩阵进行分解，降维后获得特征向量
如何有效并且高效地表示图这一复杂数据结构
Given a network/graph $G=(V,E,W)$, where $V$ is the set of nodes, $E$ is the set of edges between the nodes, and $W$ is the set of weights of the edges, the goal of node embedding is to represent each node $i$ with a vector $u_i\in R^d$, which preserves the structure of networks.

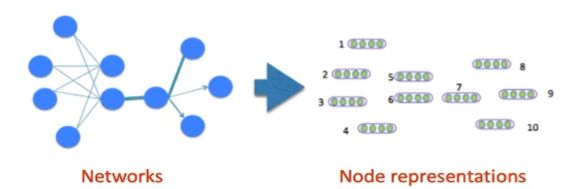
应用

网络表征后可以做很多下游任务（down-streaming tasks）：如节点分类、边预测、推荐通过文本构成网络后进行单词表征
E.g, Facebook social network->user representations (features)->friend recommendation

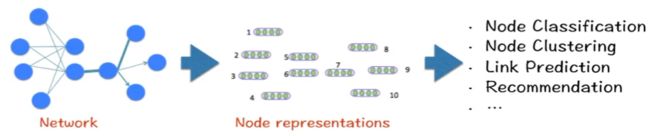
基本概念

一阶相似度：节点之间的局部相似度。但是，许多节点之间的链接是无法观察到的-sparsity.etc。1阶相似度不足以表征整个网络的结构
另外，一些动态图，图还在演化过程中，边还未生成，那么一阶相似度也不能很好描述结构。
二阶相似度：
节点邻域结构之间的接近度
“The degree of overlap of two people’s friendship networks correlates with the strength of ties between them”–Mark Granovetter
“You shall know a word by the company it keeps”–John Rupert Firth

基础知识补充

F1指标
真正例（True Positive，TP）：真实类别为正例，预测类别为正例
假正例（False Positive，FP）：真实类别为负例，预测类别为正例
假负例（False Negative，FN）：真实类别为正例，预测类别为负例
真负例（True Negative，TN）：真实类别为负例，预测类别为负例

真实类别	预测为正例	预测为负例
正例	TP	FN
负例	FP	TN

准确率（Accuracy，Acc）：
$$Acc=\frac{TP+TN}{TOTAL}$$
精确率，又称查准率（Precision，P）：
$$P=\frac{TP}{TP+FP}$$
召回率，又称查全率（Recall，R）：
$$R=\frac{TP}{TP+FN}$$
F1值：
$$F1=\frac{2\times P\times R}{P+R}$$
Macro-Fl vs Micro-F1
Macro-F1：分布计算每个类别（按ground truth的分类进行分别计算）的F1，然后做平均
Micro-F1：通过先计算总体的TP，FN和FP的数量，再计算F1

多类数据集

即网络类型有多个，任务类型也有多个。
多类网络：文本网络、社交网络、引用网络
多个任务单词推理（Word Analogy）、文本分类（Document Classification）、节点分类
（node classification）、可视化（Visualization）

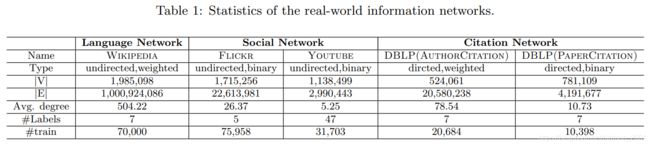
从平均degree可以知道YOUTUBE最稀疏。

研究意义

适用于任意类型的网络，有向无向、有权无权（思考DeepWalk、node2vec）。
清晰的优化目标函数，维护1st和2nd近似度。
规模化：SGD优化方法，百万级点和十亿万级的边可以在单机上几小时训练完。
是WWW2015目前引用量最高的文章。
与DeepWalk[2014]、node2vec[2016]文章一样，早期网络学习的代表性工作，经典baselines。
启发了大量基于网络结构（如triangle等）来做网络表征学习的工作。

泛读

摘要

1.提出的LINE算法适用于任意类型的信息网络：无向/有向、有权/无权。
2.LINE算法的目标函数同时保留了局部和全局的网络结构。
3.讨论算法在多个领域的网络上如单词网络、社交网络和引用网络上都验证了有效性。
4.强调了LINE算法的规模性，单机上几个小时之内可训练百万级网络。

论文标题

1. Introduction
2. Related Work
3. Problem Definition
4. LINE:Large-scale Information Network Embedding
   4.1Model Description
   4.2 Model Optimization
   4.3 Discussion
5. Experiments
   5.1 Experiments setup
   5.2 Quantitative Results
   5.3 Network Layouts
   5.4 Performance w.r.t.Network Sparsity
   5.5 Parameter Sensitivity
   5.6 Scalability
6. Conclusion

算法的比较

1.提出的顺序DeepWalk 2014，LINE 2015，Node2Vec 2016。
2.Node2Vec设置p=q=1时，等价于DeepWalk。
3.DeepWalk无太多可调的超参数（word2vec等相关参数不考虑），LINE可以选择1st order、2nd order或者组合，Node2Vec可调p、q。
4.DeepWalk和Node2Vec是基于随机游走启发的算法，LINE是基于网络结构启发的算法。

算法	Neighbor Expansion	Proximity	Optimization	Validation Data
LINE	BFS	1st or 2nd	负采样	No
DeepWalk	Random	2nd	层次softmax	No
Node2Vec	BFS+DFS	1st	负采样	Yes

LINE算法详解

KL散度

性质：非负；当且仅当p=q为0；非对称
KL散度是非负的。
当且仅当P和Q在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是“几乎处处”相同的时候，KL散度为0。
KL散度不是真的距离，它不是对称的：$D_{KL}(P||Q)\ne D_{KL}(Q||P)$
这个指标在李宏毅的课里面有讲过
假设原概率分布为$P(x)$，近似概率分布为$Q(x)$，则可使用KL散度衡量这两个分布的差异：
$$D_{KL}(P||Q)=E_{x\sim P}[\text{log}\frac{P(x)}{Q(x)}]=E_{x\sim P}[\text{log}P(x)-\text{log}Q(x)]$$
如果$x$是离散型变量，上式还可以写成如下形式：
$$D_{KL}(P||Q)=\sum _{i=1}^{N}P(x_i)\text{log}\frac{P(x_i)}{Q(x_i)}=\sum _{i=1}^{N}P(x_i)[\text{log}P(x_i)-\text{log}Q(x_i)]$$
实例

x	0	1	2	和
$P(x)$	0.36	0.48	0.16	1
$Q(x)$	0.333	0.333	0.333	1

$$\begin{array}{rl}{D}_{KL}(P||Q)& =\sum _{x\in X}P(x_i)\text{ln}\frac{P(x_i)}{Q(x_i)}\\ & =0.36\text{ln}\frac{0.36}{0.333}+0.48\text{ln}\frac{0.48}{0.333}+0.16\text{ln}\frac{0.16}{0.333}\\ & =0.0852996\end{array}$$
$$\begin{array}{rl}{D}_{KL}(Q||P)& =\sum _{x\in X}Q(x_i)\text{ln}\frac{Q(x_i)}{P(x_i)}\\ & =0.333\text{ln}\frac{0.333}{0.36}+0.333\text{ln}\frac{0.333}{0.48}+0.333\text{ln}\frac{0.333}{0.16}\\ & =0.097455\end{array}$$

交叉熵

交叉熵（cross-entropy）和KL散度联系很密切。同样地，交叉熵也可以用来衡量两个分布的差异
非负
和KL散度相同，交叉熵也不具备对称性
对同一个分布求交叉熵等于对其求熵。
$$H(P,Q)=-E_{x\sim P}\text{log}Q(x)$$
同样，离散变量的时候：
$$H(P,Q)=-\sum _{i=1}^{N}P(x_i)\text{log}Q(x_i)$$
有了这个定义，那么KL散度公式变成：
$$\begin{array}{rl}{D}_{KL}(P||Q)& =\sum _{i=1}^{N}P(x_i)[\text{log}P(x_i)-\text{log}Q(x_i)]\\ & =\sum _{i=1}^{N}P(x_i)\text{log}P(x_i)-\sum _{i=1}^{N}P(x_i)\text{log}Q(x_i)\\ & =-[-\sum _{i=1}^{N}P(x_i)\text{log}P(x_i)]+[-\sum _{i=1}^{N}P(x_i)\text{log}Q(x_i)]\\ & =-H(P)+H(P,Q)\end{array}$$
在很多时候上式中的$H(P)$是常数，所以以KL散度作为优化目标，通常可以等价于优化交叉熵。
计算实例：
$P_1=[10000]$
$Q_1=[0.40.30.050.050.2]$
$Q_2=[0.980.01000.01]$
$$\begin{array}{rl}H(P_1,Q_1)& =-\sum _i{P}_1(i)\text{log}{Q}_1(i)\\ & =-(1\text{log}0.4+0\text{log}0.3+0\text{log}0.05+0\text{log}0.05+0\text{log}0.2)\\ & =-\text{log}0.4\\ & \approx 0.916\end{array}$$
$$\begin{array}{rl}H(P_1,Q_2)& =-\sum _i{P}_1(i)\text{log}{Q}_2(i)\\ & =-(1\text{log}0.98+0\text{log}0.01+0\text{log}0.+0\text{log}0+0\text{log}0.01)\\ & =-\text{log}0.98\\ & \approx 0.02\end{array}$$
把$P_1$看做是标签，我们希望模型预测效果是第一维概率越大越好。

细节一：1阶相似度推导

1阶相似度：直接邻居，只能算无向图
结合KL散度的推导
先把原文的公式搬过来：
模型计算公式（两个点之间相互连接的概率）
$$p_1(v_i,v_j)=\frac{1}{1+\text{exp}(-u_i^T\cdot u_j)}\text{\hspace{1em}(1)}$$
其中$u$是顶点$v$的embedding表示
对于ground truth的概率（$w_{ij}$是两个点之间是否相邻，$W$是所有点之间相邻的总数，分母是针对图中所有的点）：
$${\hat{p}}_1(v_i,v_j)=\frac{w_{ij}}{W}\text{, where }W=\sum _{i,j\in E}{w}_{ij}\text{\hspace{1em}(2)}$$
计算二者的KL散度，并根据公式展开，第四个等号把上面的公式1和2代入3：
$$\begin{array}{rl}{O}_1& =KL({\hat{p}}_1(v_i,v_j),p_1(v_i,v_j))\\ & =\sum _{i,j\in E}{\hat{p}}_1(v_i,v_j)[\text{log}{\hat{p}}_1(v_i,v_j)-\text{log}{p}_1(v_i,v_j)]\\ & =\sum _{i,j\in E}{\hat{p}}_1(v_i,v_j)\text{log}{\hat{p}}_1(v_i,v_j)-\sum _{i,j\in E}{\hat{p}}_1(v_i,v_j)\text{log}{p}_1(v_i,v_j)\\ & =\sum _{i,j\in E}\frac{w_{ij}}{W}\text{log}\frac{w_{ij}}{W}-\sum _{i,j\in E}\frac{w_{ij}}{W}\text{log}{p}_1(v_i,v_j)\end{array}\text{\hspace{1em}(3)}$$
当网络固定的时候$w_{ij},W$都是固定的，是常数
$$O_1=-\sum _{i,j\in E}{w}_{ij}\text{log}{p}_1(v_i,v_j)$$
实际上，二者的KL散度就是交叉熵的公式，注意上式中$w_{ij}$不能省略因为不同顶点$w_{ij}$不一样，而$W$作为总的权重是不变的。

细节二：2阶相似度推导

2阶相似度：邻居间的比较，可以算有向图$v_j|v_i$表示从i到j的二阶相似度。顶点i可以看做是中心词，j可以看做是周围词。
结合KL散度的推导。

For each directed edge ($i,j$),we first define the probability of “context” $v_j$ generated by
vertex $v_i$ as:模型计算2阶相似度（预测值）：
$$p_2(v_j|v_i)=\frac{\text{exp}({u^{\prime }}_j^T\cdot u_i)}{{\sum }_{k=1}^{|V|}\text{exp}({u^{\prime }}_j^T\cdot u_i)}\text{\hspace{1em}(4)}$$
其中$|V|$是图中节点数量
对于ground truth的概率
$${\hat{p}}_2(v_j|v_i)=\frac{w_{ij}}{d_i}\text{\hspace{1em}(5)}$$
$d_i$是顶点$v_i$的出度。
有了模型计算值和ground truth的概率分布，就可以算二者的KL散度（其中${\lambda }_i$是节点i的重要程度，可以通过节点i的出入度数量来判断，原始应该是pagerank算法进行排序）【第三个等号将公式4和5代入】：
$$\begin{array}{rl}{O}_2& ={\lambda }_{i}KL({\hat{p}}_2(v_j|v_i),p_2(v_j|v_i))\\ & =\sum _{i\in V}{\lambda }_i{\hat{p}}_2(v_j|v_i)(\text{log}{\hat{p}}_2(v_j|v_i)-\text{log}{p}_2(v_j|v_i))\\ & =\sum _{i\in V}{\lambda }_i\frac{w_{ij}}{d_i}[\text{log}\frac{w_{ij}}{d_i}-\text{log}{p}_2(v_j|v_i)]\end{array}$$
这里作者用${\lambda }_i=d_i$代入上式：
$$\begin{array}{rl}{O}_2& =\sum _{i\in V}{w}_{ij}[\text{log}\frac{w_{ij}}{d_i}-\text{log}{p}_2(v_j|v_i)]\\ & =\sum _{i\in V}{w}_{ij}\text{log}\frac{w_{ij}}{d_i}-\sum _{i\in V}{w}_{ij}\text{log}{p}_2(v_j|v_i)\end{array}$$
图结构确定后，$w_{i}j，d_i$是常数，因此第一项是常数：
$$O_2\approx -\sum _{i\in V}{w}_{ij}\text{log}{p}_2(v_j|v_i)\text{\hspace{1em}(6)}$$

细节三：负采样的推导

由于公式6中可以看到有一项是$p_2(v_j|v_i)$，这个是针对图中所有顶点两两之间进行计算，复杂度为$O(n^2)$，为了简化计算，使得模型能够在大规模图数据上运行，模型引入了负采样简化计算。同样情况还出现在了公式4的分母$\text{exp}({u^{\prime }}_j^T\cdot u_i)$

w代表当前单词或者当前节点
c代表上下文或者邻居节点
D代表一个集合（可以看做训练集数据）
$$arg\underset{\theta }{\max }\prod _{(w,c)\in D}p(D=1|c,w;\theta )\prod _{(w,c)\notin D}p(D=0|c,w;\theta )$$
上式的意思是要找到一个参数$\theta$，使得当$w,c$属于集合D（出现在训练集中）的时候，P的概率最大化，当$w,c$不属于集合D（没有出现在训练集中）的时候，P的概率最小化
$$=arg\underset{\theta }{\max }\prod _{(w,c)\in D}p(D=1|c,w;\theta )\prod _{(w,c)\notin D}(1-p(D=1|c,w;\theta ))$$
连乘变连加，取log：
$$=arg\underset{\theta }{\max }\sum _{(w,c)\in D}\log p(D=1|c,w;\theta )+\sum _{(w,c)\notin D}\log (1-p(D=1|c,w;\theta ))$$
将概率用sigmoid或softmax公式代入，其中$v_c,v_w$是c和w对应的embedding：
$$\begin{gathered} =arg\underset{\theta }{\max }\sum _{(w,c)\in D}\log \frac{1}{1+e^{-v_c\cdot v_w}}+\sum _{(w,c)\notin D}\log (1-\frac{1}{1+e^{-v_c\cdot v_w}}) \\ =arg\underset{\theta }{\max }\sum _{(w,c)\in D}\log \frac{1}{1+e^{-v_c\cdot v_w}}+\sum _{(w,c)\notin D}\log (\frac{1}{1+e^{v_c\cdot v_w}}) \end{gathered}$$
根据sigmoid的定义：$\sigma (x)=\frac{1}{1+e^{(-x)}}$，上式可以写成：
$$=arg\underset{\theta }{\max }\log \sigma (v_c\cdot v_w)+\sum _{(w,c)\notin D}\log \sigma (-v_c\cdot v_w)$$

然后为了和论文的公式7一样，我们令：$v_c={u^{\prime }}_j^T,v_w=u_i$
$$=arg\underset{\theta }{\max }\log \sigma ({u^{\prime }}_j^T\cdot u_i)+\sum _{i=1}^K{E}_{v_n\sim p_n(v)}\log \sigma (-{u^{\prime }}_j^T\cdot u_i)\text{\hspace{1em}(7)}$$
加号后面那项就表示不存在的边，也就是负样本，K代表采样的个数。这个个数应该是和$v_n$这个节点的度$p_n(v)$有关。

细节四：alias table

梯度下降学习率优化
对于二阶相似度：
$$O_2\approx -\sum _{i\in V}{w}_{ij}\text{log}{p}_2(v_j|v_i)\text{\hspace{1em}(6)}$$
求其对$u_i$的偏导：
$$\frac{\partial O_2}{\partial u_i}=w_{ij}\cdot \frac{\partial \text{log}{p}_2(v_j|v_i)}{\partial u_i}$$
可以看到这里$w_{ij}$又是对所有的点进行计算，作为权重有大有小，大的时候会出现梯度爆炸，小的时候梯度会消失，学习率不好设置。
A simple treatment is thus to unfold a weighted edge into multiple binary edges, e.g., an edge with weight w is unfolded into w binary edges.
就是有邻接关系就设置为1，没有就设置为0.但是这样按邻接矩阵来存储对内存消耗比较大。
作者这里也按$w_{ij}$进行正比来对边进行采样计算，不对所有边进行计算。
不展开，具体到Node2Vec具体讲。
总体时间复杂度为：$O(dK|E|)$
这里的K就是公式7中负采样的边数量
d是embedding的维度
一条正样本边对应K条负样本的边，其时间复杂度为：$O(d(K+1))\sim O(dK)$
总共有$|E|$条边，优化的步数时间复杂度为：$O(|E|)$
上面两个相乘得到最后结果：$O(dK|E|)$

细节五：低度点的处理Low degree vertices

低度点：难以学习，因为度低邻居数少2阶相似度难学，用高阶信息补充（补充后就看做是直接邻居），这里面采用的是邻居的邻居
新点：保持其他点的embedding不变，计算新点的embedding
新点其他的处理方法：GraphSage模型（后面讲，主要处理动态图）

实验结果及分析

数据集

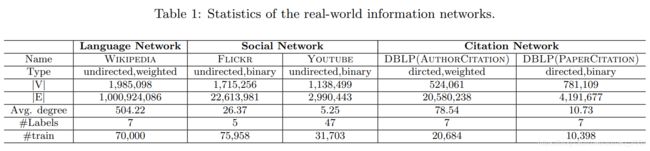
三类数据集。
wikipedia数据集上的单词类比实验

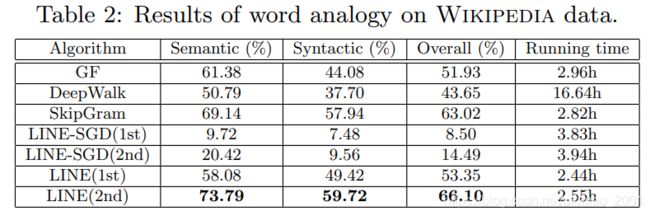
wikipedia数据集上的文本分类实验 document classification：
one-vs-rest logistic regression classifier：二分类器，七个分类要训练七个分类器。取某一个分类为一类，其他六类为一类，得到某一个分类的打分，如此做七次，得到七个打分，取最高者作为当前分类的预测结果。

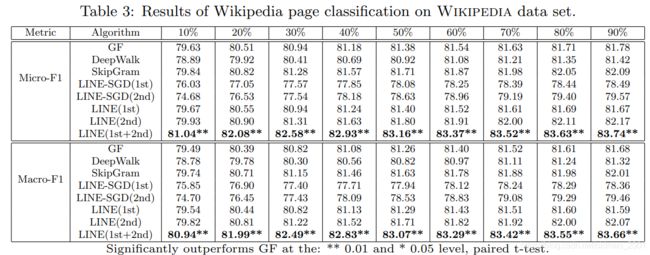
社交网络比较稀疏，因此一阶相似度比二阶相似度重要（从实验数据可以看到）
Flicker数据集上的节点分类实验 Node classification

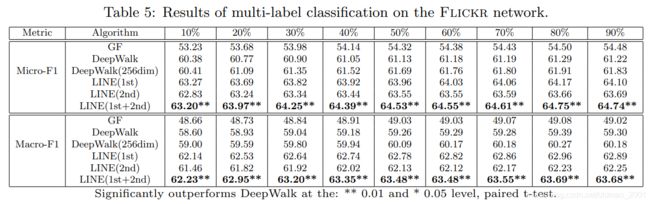
下图中，括号里面的数据是将稀疏的图中的节点通过邻居的邻居进行加边扩展（邻居上限为1000，超过性能并无提升。）后做的效果（下同）。

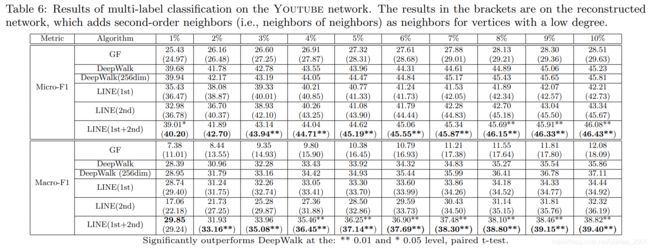
DBLP（作者网络）数据集上的节点分类实验 Node classification

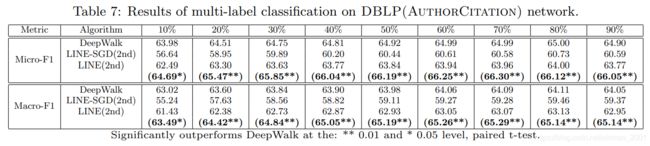
DBLP（论文网络）数据集上的节点分类实验Node classification

TSNE可视化，三类会议： WWW, KDD from “data mining,” NIPS, ICML from “machine learning,” and CVPR, ICCV from “computer vision.”

参数实验（略）

论文总结

关键点
图的一阶和二阶相似度的理解
图的一二阶相似度转化为目标函数
公式的推导
时间复杂度分析
图上的负采样，alias sampling
创新点
根据图的信息直接建模
不基于random walk
大规模数据集上的应用
丰富的实验论证效果
启发点
图的理解对网络表征学习的作用
基于图的结构启发了大量的工作（triangle、clique）
本文的作者Jian Tang老师是图机器学习的著名研究员，大家可以关注
算法的设计，通过KL散度将基于图结构的预测值和真实值进行比较
复杂时间复杂度分析
算法优化方法的选择

#代码复现（待填坑）

问题

负采样推导倒数第二行的第一项的求和怎么不见了？最大化参数为什么没有出现在最后公式中？
如果图比较稀疏，那么节点大多数都没有邻居，那么它们的二阶相似度都一样？是如何解决这个问题？
欢迎留言讨论