Python+机器学习的学习日记（2020.4.17-2020.4.21）

2020.4.17

学习了《Python编程 从入门到实践》 第二章

对字符串的首字母大写、全部大写、全部小写的操作

message.upper()
message.lower()
message.title()

去除字符串首端的空白、末端的空白、同时去除首尾的空白

message.lstrip()
message.lstrip()
message.strip()

粗略阅读Python之禅

学习了 李宏毅2020机器学习 Regression、误差来源、Gradient Decent部分

（小部分内容摘抄自：
the github page is: https://Sakura-gh.github.io/ML-notes）

Regression部分从预测口袋妖怪的战斗力开始引入，讲解了线性回归的基本原理，梯度下降的基本原理。随后讲解了利用高次方程来拟合一个更为复杂的曲线模型，越高次的方程越能更好的匹配训练集，但是也正是因为太过依赖于训练集，导致泛化性能不好，在测试集的表现中就非常不好，这就是过拟合。而欠拟合则是方程过于简单，对无论是测试集还是训练集来说都不能很好的进行匹配，这就是欠拟合。

在模型中加入了正则化的因子来限制模型中权重值的大小，是权重值尽可能的小，这样逼迫拟合出来的曲线趋近于平滑，从而有更强的泛化性能和抗噪声特性。当然正则化因子的选择也是有一个度的，当这个值过于小，对于曲线模型就不能起到平滑的作用，所以训练集中的噪声对模型的影响就很大，也就是模型过拟合，泛化能力差。那么相对的，当正则化因子过大，曲线过于平滑，则会导致欠拟合。

误差主要是来源于Bias和Variance，中文不知道怎么翻译算合适。图片表达的很直观：

这里涉及到一些统计学的内容，学习之后需要再次观看。

经过多次取样之后，对每一组样本进行线性回归，然后分以下2种情况：
1.如果使用简单的方程对这机组样本分别进行线性回归，可以发现这些曲线都是比较平滑的，并且聚的比较紧，这样的一组曲线他的Variance是比较小的。同时这些曲线的平均值所形成的曲线也是比较平滑的，但这样的平均值曲线是欠拟合的，所以它与真实的曲线（就是能产生样本的那个曲线）之间是有Bias的，而且曲线越平滑Bias就越大，这种情况局对应的左下角的图像。

2.如果使用复杂的方程对这机组样本分别进行线性回归，可以发现这些曲线都是比较弯弯曲曲，并且分散的很开，这样的一组曲线他的Variance是比较大的。同时这些曲线的平均值所形成的曲线也是比较弯曲的，但这样的平均值曲线是跟贴近真实曲线（就是能产生样本的那个曲线）的，所以它的Bias就会小，，这种情况局对应的右上角的图像。

所以选择模型应该综合考虑Bias和Variance这两个误差，取到一个比较中和的值。当Variance大的时候，说明你的模型过拟合了，可以增加更多的样本，或者引入正则化。当Bias大的时候，说明你的模型欠拟合了，可以增加更多的特征，或者使用更高次数的方程来代替你的模型。

随后还介绍了n折交叉验证的操作方法。

Gradient Decent部分介绍了learning rate的自适应改变方法，因为learning rate过小可能导致模型计算过于缓慢，learning rate过大则会导致梯度下降步子太大，直接越过最低点，无法得到loss function的最小值，所以要选择自适应的learning rate。

Adagrad是learning rate的自适应方法，在gradient descent中，我们希望微分值越大(斜率越大)更新的步伐要更大一些，因为这个时候表示离loss function的最低点还远。但是Adagrad的表达式中，分母表示梯度越大步伐越大，分子却表示梯度越大步伐越小，两者似乎相互矛盾。这其实是因为gradient越大，离最低点越远这件事情在有多个参数的情况下是不一定成立的。

可以看到a点离最小值点更远，但是微分却小。b点离最低点近，而微分更大。这种情况下就直接考虑最优步长的问题了。

面对loss function是一个椭圆时，通常要考虑Adagrad，因为正如图像中w1和w2的方向，在同一点处，两个方向的微分和它们距离最低点的距离并不是成正比的。

接下来是Stochastic Gradicent Descent（随机梯度下降），传统的梯度下降算法在进行loss 评估时，要将目前这个模型与所有样本点比对，大大增加了时间。而Stochastic Gradicent Descent只是随机选取一个样本点进行loss分析。如果有20个样本点，传统Gradicent Descent下降一步，Stochastic Gradicent Descent已经下降了20步，这种方法的最大优点就是快。

Feature Scaling(特征缩放)的思想是：样本的有些特征，转换为数字后很大，如房屋的面积。而有些特征转换为数字后又会很小，比如卫生间的个数。这样我们在对一个房屋价格进行预测（对收集到的房屋样本的特征对价格进行线性回归）时，这两种特征如果不加处理就放入模型，对模型而言是不好的。以为面积这个特征相对于卫生间的个数来说，二者的数值相差太大，导致loss function的俯视图从一个正圆，变到一个椭圆，而且这两个特征的数值差距越大，这个椭圆就更加椭。这样的结果前面已经说过，就要使用Adagrad。而且如果loss function是一个正圆的话，对模型的效率也是有提升的。

最后是利用Taylor Series（泰勒级数）来进行梯度下降。对于一个loss function（这里默认无穷阶可导）我们可以用Taylor Series来近似它，并且近似的级数越高，近似收敛域也越大（也就是近似函数与原函数相等的区域越大），所以我们可以使用Taylor Series在收敛域内求得loss function的最小值，然后一步一步逼近全局最小值。

2020.4.18

学习了《Python编程 从入门到实践》 第三章

学习了构建Python中的列表，访问其中的元素

#创建列表
names=['shanghai','chengdu','hangzhou']
#访问其中第二个元素
names[1]

向列表中修改、添加、删除元素

#修改其中第二个元素为'xian'
names[1]='xian'
#向列表最后增加元素'shenzhen'
names.append('shenzhen')
#向任意位置(选三号位)增加元素'qingdao'
names.insert(2,'qingdao')
#按位置删除
del names[1]
#删除之后还需使用
v=names.pop(1)
#根据值删除
names.remove('shanghai')

组织列表，列表排序是按首字母和首数字大小进行的

#永久性排序
names.sort()
#永久性倒序排序
names.sort(reverse=True)
#临时排序
names.sorted()
#l临时性倒序排序
names.sorted(reverse=True)
#永久在现有顺序上进行倒序
names.reverse()

获取列表长度

len(names)

学习了 李宏毅2020机器学习Classification: Probabilistic Generative Model部分

（小部分内容摘抄自：
the github page is: https://Sakura-gh.github.io/ML-notes）

这部分的学习真的让人回味无穷，醍醐灌顶。

课程根据口袋妖怪的各种属性（生命值，防御力，速度，特攻，特防…），来将口袋妖怪归类到不同的系（草，水，火，飞行，格斗，钢铁…）。个人觉得这个分类不可能太成功，因为每个系都有不同类型的口袋妖怪，就像每个系里都有擅长防御的妖怪，也有擅长攻击的妖怪，所以各种属性在各个系中的分布应该是差不多的，但是李宏毅老师最后还是做出了70%多的正确率，看来数据中隐藏的东西确实是有很多。

为了方便，就取通用系和水系两种妖怪来做实验。然后在各种属性里面取两个属性作为一个样本的基本属性。接下来画出两个系的样本分布图，应该是两个不同的散点图。那么之后再来一个新样本，我们也可以把它画到相应的散点图中去。

这两个散点图画出来以后，一定是有密有疏的，密集的地方代表这个地方出现的样本点，大概率属于这个系。那么对于新来的样本点来说，我们就可以根据它所处的位置的样本点疏密程度，来判断新样本点属于该系的概率大小，有点概率密度的意思。

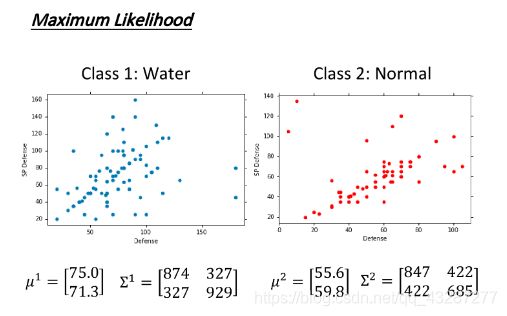
两幅散点图，我们都可以认为都是从一个高斯分布中抽样而来（也可以是别的分布，这个可以根据个人喜好和实际情况而定）。那么这样一来，我们就可以根据现有的训练样本来确定出最符合抽样结果的那个高斯分布（就是找出一个高斯分布，在这个模型上抽样，抽到现有的这么多训练样本的概率是最大的），其实就是最大似然估计。最后得到水系和通用系的两个高斯分布模型。

有了这两个模型之后我们就借助贝叶斯概率：

c1代表水系，c2代表通用系，等式是左边的p表示，x是来自水系的概率。现在p（x|c1）和p（x|c2）都已经知道（根据前面的高斯模型得出）。因为训练样本中有79只水系，61只通用系，所以p（c1）是79/(79+61)，p（c2）以此类推。那么至此p（c1|x）的概率也知道了。把概率值的图画出来就是左上角那个，以0.5作为分界线就是右上角那个：

概率论与数理统计学过，确定一个高斯分布，需要知道mu和sigma，mu决定它的顶点位置，sigma决定它的胖瘦、拉伸。我们之前得到的水系和通用系的mu和sigma都是不一样的，其实我们可以只将mu设置不同，而sigma让两者相同，这样的话，上面模型中的0.5分界线就会变成直线，接下来就是最闪光的时刻。

我们分析贝叶斯概率公式，可以得到如下结果：

这就是大名鼎鼎的sigmoid函数的由来。

再将图中的z化简，得到如下结果：
当两个高斯模型共用sigma的时候，就变成了一个线性模型，这样就解释了上面分界线变成直线的现象了。

这样子其实有点复杂，因为绕了一大圈，又求mu又求sigma，回来还是求w和b，明天将介绍直接求解w和b的方法。

2020.4.19
今日出门、头疼，只学了Python。

学习了《Python编程 从入门到实践》 第四章

#遍历整个列表
place=['shanghai','guangzhou','shenzhen','beijing','xian']
for i in place:
    print(i)

其中i是作为临时变量存在的。注意不要忘记缩进和冒号。

range()函数的用法：

#规定循环次数
for i in range(1,5)
    print(i)
#结果是打印1到4。

#使用range()创建数字列表
numbers=list(range(1,5))
#结果是[1，2，3，4]

对列表进行简单的计算：

#就是字面意思
sum(numbers)
min(numbers)
max(numbers)

列表切片：

number[0:3]   #表示numbers中第一到第三个元素
number[-3:]    #表示numbers中倒数第三到最后

遍历切片：

for i in numbers[3:]     
    print(i)      # 表示打印numbers中第二个到最后的元素们

复制列表：

numbers_ok=numbers[:]   #注意不能使用 numbers_ok=numbers 这样其实是两个变量指向了同一个列表。

Python中的元组使用小括号()来定义，元组不可修改，但是可以对元组变量名进行重新赋值，也可以同列表一样使用便利操作。

2020.4.20

学习了《Python编程 从入门到实践》 第五章

这一章Python的主要内容是if语句的使用，很简单就不再多说了。
检查特定值是否包含在列表中：

'shanghai' in place
'shanghai' not in place

检查列表是不是空的：

place=[]
if place:
     ...
else:
     print('这是个空列表')

2020.4.21

学习了《Python编程 从入门到实践》 第六章

这一章的主要内容是字典。
首先是创建字典，字典使用花括号创建，每一项包括一个健和一个值，键和值之间使用冒号分割，每一项之间使用逗号分割。

sun={
     'name':'sun','age':18,'home':'xinjiang'}

访问字典中的值

sun['name']

添加键值对

sun['glass']=True

删除键值对

del sun['age']

遍历字典

for key,value in sun.items()

遍历字典中的健、值

for key in sun.keys()

for value in sun.values()

多个字典可以存放在列表里，列表也可以作为值存放在字典里，字典也可以作为值存放在字典里。