相位解包裹（七）多频法相位解包裹（multi-frequency phase unwrapping）

之前讲了两种经典的空间相位解包裹算法，从这篇文章起就在介绍两种时间相位解包裹的算法。

首先先复习一下时间相位解包裹的基本原理和优势。

时间相位解包裹是根据同一位置（像素）不同时间得到的相位图来进行相位解包裹，获得的相位被称为绝对相位。在时间相位解包裹过程中，每个点的相位只与不同频率的相位图上同一位置的点有关，与其邻点无关，因此即使某点的相位由于相位混叠、相位噪声导致解包裹错误，这样的错误并不会传递。

空间相位解包裹是在同一张相位图中解包裹，所以错误会传递；时间相位解包裹是在时间序列上解包裹，所以错误不会在空间中传递。

 

 

多频法相位解包裹multi-frequency (hierarchical) phase unwrapping

时间相位解包裹也包含多种算法，首先讲的是多频法相位解包裹multi-frequency (hierarchical) phase unwrapping。从英文名字看，我觉得还可以翻译成分级相位解包裹，顾名思义，这个方法是用多个频率的相位图分级进行相位解包裹。

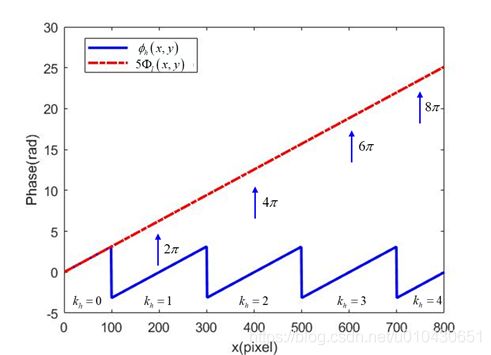
多频法相位解包裹，即投影多个不同频率的正弦条纹图样到被测物体上，分别提取出各频率正弦条纹图样的截断相位。同时要求频率最小（周期最大）的条纹图样一个周期就可以覆盖整个被测物体，则该频率条纹图样的相位不需要相位解包裹，其截断相位就已经等于连续相位

已知低频条纹的连续相位，如上图，根据下面两个式子，可通过低频条纹的连续相位解包裹高频条纹的截断相位，逐级恢复出最高频条纹的连续相位

以上两式中，下标表示高频条纹，下标表示低频条纹，表示条纹的波长。

 

相比空间相位解包裹，时间相位解包裹的方法原理要简单很多，算法实现也非常简单。

 

实验结果

放一个我做的结果，一共用了4个频率的条纹图样，三步相移提取相位，多频法解包裹相位。

 

 

多频法的小升级

多频法还有个小升级，我把相关文献放出来，在[6]、[7]，有兴趣可以去看一看。

该方法可以叫做几何约束(Geometrical constraint)的多频分级法 ，原理基本类似多频法。区别在于多频法相位解包裹中，初始的连续相位图是从一个周期就可以覆盖整个被测物体的频率很小（周期很大）的条纹图样中获取的，而几何约束的多频法相位解包裹中，初始的相位图是通过基于双目视觉的结构光系统标定获得相位——深度映射（我的文章后面也会讲到），根据该映射关系计算出某一深度时的连续相位图，根据该相位图，逐级解包裹高频条纹的截断相位，最后恢复出最高频条纹的连续相位。

由于原理基本一样，这里就不细讲了，主要是我还没体会到这种做法的优势在哪（来自学渣的提问）Orz

 

 

 

 

参考文献：

[1] Ghiglia D C, Pritt M D. Two-dimensional phase unwrapping: theory, algorithms, and software[M]. New York: Wiley, 1998.

[2] Zhang S. Absolute phase retrieval methods for digital fringe projection profilometry: A review[J]. Optics and Lasers in Engineering, 2018, 107: 28-37.

[3] Zuo C, Huang L, Zhang ML, et al. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review[J]. Optics and Lasers in Engineering, 2016, 85: 84-103.

[4] Zhang S. Digital multiple wavelength phase shifting algorithm[C]//Optical Inspection and Metrology for Non-Optics Industries. International Society for Optics and Photonics, 2009, 7432: 74320N.

[5] Hyun J S, Zhang S. Enhanced two-frequency phase-shifting method[J]. Applied optics, 2016, 55(16): 4395-4401.

[6] An Y, Hyun J S, Zhang S. Pixel-wise absolute phase unwrapping using geometric constraints of structured light system[J]. Optics express, 2016, 24(16): 18445-18459.

[7] Dai J, An Y, Zhang S. Absolute three-dimensional shape measurement with a known object[J]. Optics express, 2017, 25(9): 10384-10396.

 

 

声明：本文中的图片、公式等都和作者本人的毕业论文有关，如果抄袭盗用吃亏是你自己哦~实在有需要，这里建议你自己码一下公式，自己做一下相关的图哦亲。作者水平有限，如文中有错，请务必留言指正。如有学习交流需要，也可通过邮箱[email protected]联系我，大家一起讨论学习。