时间序列的总结
总结工作中用到的时间序列相关内容。
1、指数平滑的理论
指数平滑
R实践
# 基础包里的函数HoltWinters()
# 非季节性简单指数平滑 — models level(即上面简单指数平滑法)
fit <- HoltWinters(myts, beta=FALSE, gamma=FALSE)
# 非季节性性趋势模型 - models level and trend
fit <- HoltWinters(myts, gamma=FALSE)
# 季节性序列分解- models level, trend, and seasonal components
fit <- HoltWinters(myts)
gamma 对应季节性;belta代表趋势斜率;alpha代表平滑系数,当alpha越接近0,临近预测的观测值在预测中的权重就越小【注意,这里与excel不同】。
2、自回归模型(AR):
X t = α 1 X t − 1 + α 2 X t − 2 + . . . + α p X t − p + u t X_t = \alpha_1X_{t-1} + \alpha_2X_{t-2} +...+ \alpha_pX_{t-p} + u_t Xt=α1Xt−1+α2Xt−2+...+αpXt−p+ut
当随机扰动项是一个白噪声( u t = ε t u_t = \varepsilon_t ut=εt),则称为一个纯AR(p)过程,记为:
X t = α 1 X t − 1 + α 2 X t − 2 + . . . + α p X t − p + ε t X_t = \alpha_1X_{t-1} + \alpha_2X_{t-2} +...+ \alpha_pX_{t-p} + \varepsilon_t Xt=α1Xt−1+α2Xt−2+...+αpXt−p+εt
自回归模型首先需要确定一个阶数p,表示用几期的历史值来预测当前值。
自回归模型有很多的限制:
(1)自回归模型是用自身的数据进行预测
(2)时间序列数据必须具有平稳性
(3)自回归只适用于预测与自身前期相关的现象(时间序列的自相关性)
自相关系数PACF(p)
3、 滑动平均模型(MA):
u t = ε t + β 1 ε t − 1 + . . . + β q ε t − q u_t = \varepsilon_t + \beta_1\varepsilon_{t-1}+...+\beta_q\varepsilon_{t-q} ut=εt+β1εt−1+...+βqεt−q,其中 ε t \varepsilon_t εt表示白噪声序列。
特别的,当 X t = u t X_t = u_t Xt=ut,即时间序列当前值与历史值没有关系,而只依赖于历史白噪声的线性组合,就得到MA模型:
X t = ε t + β 1 ε t − 1 + . . . + β q ε t − q X_t = \varepsilon_t + \beta_1\varepsilon_{t-1}+...+\beta_q\varepsilon_{t-q} Xt=εt+β1εt−1+...+βqεt−q
4、自相关滑动平均模型(ARMA)
将AR(P)与MA(q)结合,得到一个一般的自回归移动平均模型ARMA(p,q):
X t = α 1 X t − 1 + α 2 X t − 2 + . . . + α p X t − p + ε t + β 1 ε t − 1 + . . . + β q ε t − q X_t = \alpha_1X_{t-1} + \alpha_2X_{t-2} +...+ \alpha_pX_{t-p} + \varepsilon_t + \beta_1\varepsilon_{t-1}+...+\beta_q\varepsilon_{t-q} Xt=α1Xt−1+α2Xt−2+...+αpXt−p+εt+β1εt−1+...+βqεt−q
5、 ARIMA模型
将自回归模型(AR),滑动平均模型(MA),差分结合,就形成了ARIMA(p,d,q),其中p,d,q三个参数的确认,也是时间序列模型最难的部分。
6、 组合模型
时间序列趋势主要受到长期趋势(T)、季节变动(S)、周期波动(C)和不规则波动(I)四个因素影响,可构建
加法模型: x t = T t + S t + C t + ε t x_t = T_t+S_t+C_t+\varepsilon_t xt=Tt+St+Ct+εt
乘法模型: x t = T t ∗ S t ∗ C t ∗ ε t x_t = T_t*S_t*C_t*\varepsilon_t xt=Tt∗St∗Ct∗εt
7、示例
已知15年至18年逐月的交易额,且已知部分月份做过大型促销活动,现面临19年业务预算,请按照时间序列给出19年的逐月交易预估,作为预算建议。
GMV2<- read_excel("D:develop\\GMV_ts2.xlsx")
View(GMV2)
GMV2_ts=ts(GMV2[,2],start=c(2015,1),frequency = 12)
GMV2_ts=GMV2_ts[,1]
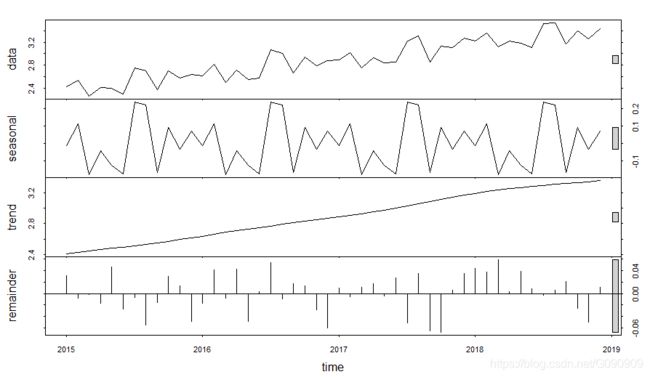
plot(stl(GMV2_ts,s.window='period'))
auto.arima(GMV2_ts)
GMV2_ts_ts=arima(GMV2_ts,order=c(0,0,0),seasonal=list(order=c(1,1,0),period=12))
GMV2_ts_ts
plot(GMV2_ts_ts$residuals)
abline(h=0)
qqnorm(GMV2_ts_ts$residuals)
qqline(GMV2_ts_ts$residuals)
GMV2_fo=forecast(GMV2_ts_ts,12)
plot(GMV2_fo)
判断通过R的auto.arima()计算参数p,d,q

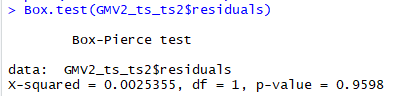
残差检验
模型的预测结果:

这里观测预测出来的序列波动,发现与已知业务波动趋势变化较大,因此需要重选参数p,d,q。
使用R自带的ADF检验来判断d,ACF()、PACF()来判断q和p。