数据结构与算法之哈希表

数据结构与算法系列文章

数据结构与算法之哈希表

数据结构与算法之跳跃表

数据结构与算法之十大经典排序

数据结构与算法之哈希表

该系列为博主自己学习记录数据结构与算法的实现。
本篇文章主要介绍哈希表（Hash Table，又称散列表）的原理、部分源码、以及练习实现。

一、哈希表原理

该部分主要用于介绍哈希表相关概念与原理。

(一)、概念

1. 哈希表定义

哈希表，又称散列表，英文名为Hash Table。实质上是一种对数组进行了扩展的数据结构，可以说哈希表是在数组支持下标直接索引数据(value)的基础上进行优化并尽可能在常数时间内对数据进行增、删、改、查等操作。
这一标准具有唯一性 ，我们称为键值key，比如，在学校里我们的学号是我们的唯一标识，在社会我们的身份证号码是我们的唯一标识，而哈希表就是通过某一种手段将这一唯一标识转化(也可以成为映射)为哈希表中的索引下标，如下图中唯一标识123456映射成了3，345215映射成了4等等。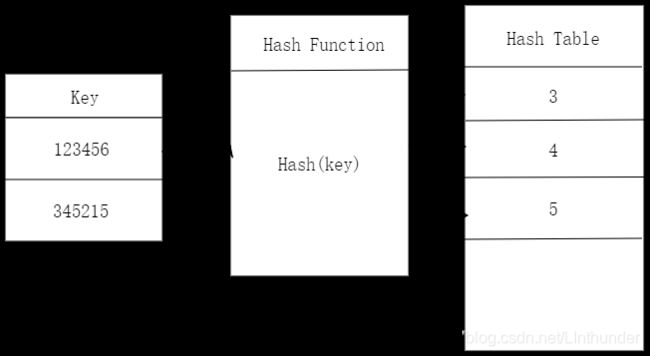

2. 哈希函数

哈希表就是通过某一种手段将这一唯一标识转化(也可以成为映射)为哈希表中的对应位置。而则这一手段/映射方法就称为哈希函数(Hash Function)，其输入参数为键值(key)。

3. 哈希冲突

不管什么数据结构，存储空间都是有限的，也就是说存储的数据量是一定的，那么当要存储的数据量超过这一数据结构当前容量(capacity)，就会发生至少两个键值对应在哈希表的同一个位置。比如，哈希表中有十个位置，那么现在要存放十一个数字到十个位置，即至少有两个数字会存放到同一个位置，这也就是鸽巢原理(抽屉原理)。

(二)、哈希函数的设计

1.哈希函数部分源码

哈希函数的实现设计决定了最后我们的哈希表中元素排列。下面为哈希函数设计源码

static final int hash(Object key) {
     
   int h;
   return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
//d字符串的哈希值计算
public int hashCode() {
     
  int var1 = this.hash;
  if(var1 == 0 && this.value.length > 0) {
     
    char[] var2 = this.value;
    for(int var3 = 0; var3 < this.value.length; ++var3) {
     
      var1 = 31 * var1 + var2[var3];
    }
    this.hash = var1;
  }
  return var1;
}

上述为其中一种哈希函数的设计，其主要是通过对容量取余来进行映射，对于字符型的键值先按位进行一个多项式计算再进行容量取模。
此处也可以看出，哈希函数的设计并不复杂，不复杂主要是为了不在计算哈希值时浪费太多的时间，这只是一种设计方式，你也可以设计其他形式的哈希函数。

2.源码哈希函数中一些细节探究

如上图所示，hashCode返回值为32位，即可以映射2³²=4*10⁹个下标，哈希函数的映射在此情况下映射较为均匀，但是如果直接申请这么大的数组，则会直接内存爆掉，因此进行了下面的操作

(h = key.hashCode()) ^ (h >>> 16)

该步骤将hashCode的高16位移至低16位然后与原低16位哈希码进行混合，哈希码的随机性进一步加大，同时注意到有得到的hashCode如果有一位变化则哈希值就会改变。这同样减小了冲突的可能。

int index = hash(key)&(capacity-1);

此处计算了index即为在哈希表中的位置，进行按位与操作，即进行了取余操作,这种操作会效率更高一些。
例子：
0110 1110 1101 0111 & 0000 0000 0000 1111 = 0000 0000 0000 0111
28375%16 = 7

index = hash(key)%capacity

哈希函数确定后，剩下的就是如何解决鸽巢原理的问题即哈希冲突的解决办法。
引申：为什么HashMap的数组长度必须是2的次幂
因为只有这样，与capacity-1进行与操作才能够是正常的取模操作。上述即为例子。

3.哈希函数设计

所以，如果我们要设计哈希函数，要保证两点才是一个较为便捷的哈希函数。
(1). 哈希函数不能过于复杂，以防止在计算哈希值处花费太多时间。
(2). 生成的哈希值要尽可能分布均匀且随机，以减小哈希冲突发生的概率。

(三)、哈希冲突的解决

目前来说，哈希冲突的解决方法有两大类链表寻址法(Linking Addressing)和开放寻址法（Opening Addressing）。

1. 链表寻址法(Linking Addressing)

如上图所示即为链表寻址法的精髓，哈希函数将键值映射到哈希表中的每个位置，我们称之为桶(bucket)/槽(slot)而每个桶中会对应一个链表，将哈希值相同的键值数据放到相应桶中即可。链表插入的好处就不用多说了，节点使用时再申请，较好的利用了空间。
当插入时，哈希函数计算到相应的桶，然后头节点或者尾节点插入即可，在java的HashMap（与HashTable有区别，但是大致近似）中，Java7叫Entry而Java8中叫Node，而在java8以前使用的是头插法，java8之后改为了尾部插入，此处与扩容机制有关，以后再介绍，今天先介绍哈希表的原理。而当进行查找或者删除操作时候，就与链表长度有关了，不多介绍。
关于插入、查找、删除等方面的时间复杂度，可以采用改变链表结构的形式(如红黑树结构)来进行优化。

2. 开放寻址法(Opening Addressing)

开放寻址法思想比较简单：如果出现一个key2进行hash(key)后映射的位置与key1进行hash(key)后映射的位置一致（即发生了哈希冲突），那么从该位置往下寻找到第一个空位时将key2的数据放入。而从该位置往下寻找空闲位置的过程又称为探测。

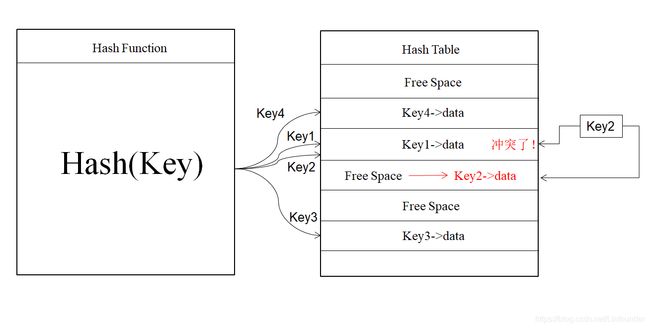
探测又主要分为三类：
(1).线性探测（Linear Probing）
线性探测即寻找空闲位置时，从当前冲突位置一个位置一个位置向下寻找:

Hash(Key)+0、Hash(Key)+1、Hash(Key)+2、Hash(Key)+3、Hash(Key)+4、Hash(Key)+5……

线性探测的方法有着很明显的弊端，就是随着空闲位置的越来越少，哈希冲突可能性增加，这就导致对哈希表进行操作时线性探测时间会加大，最坏情况下可达到O(n)，而平方探测和双重哈希就是为了减小探测时间而存在的。
(2).平方探测（Quadratic Probing）
寻找空闲位置时，从当前冲突位置按照如下方式即距离冲突位置的平方值进行探测:

Hash(Key)+0、Hash(Key)+1²、Hash(Key)+2²、Hash(Key)+3²……

平方探测：
当表大小为素数时，当表的空闲位置大于等于一半时，总能够插入一个新的元素。

(3).双重哈希（Double hashing）
寻找空闲位置时，从当前冲突位置按如下方式即采用多个哈希映射函数进行探测:

Hash1(Key)、Hash2(Key)、Hash3(Key)……

注意:
在开放寻址法中，查询一个键值的数据是否在哈希表中，如果在查找到该键值所对应的数据前遇到了空闲位置，则认定为不存在该键值，这就要求在对于一个键值所对应的哈希表中位置进行删除时，不可以直接将该桶置空，因此我们需要加上一个标志位deleted表示该位置数据已经删除，请继续往下寻找。

二、扩容机制

上面说到哈希冲突是不可避免的，并且当桶都用完了(即使是链表寻址，链表长度十分大的时候，增删改查操作也不是那么容易进行的)，新的数据就不能加进来了，这时就需要用到了扩容机制。

(一)、装载因子

而我们不可能说等到桶都装满之后才对哈希表进行扩容操作，因此我们需要找到一个阈值标准——当填入表中的元素个数达到一定值的时候就开始扩容操作。这一标准即为装载因子(load factor)。当然扩容不是那么简单的扩容，还需要重新进行哈希rehash。
因为此时就不再是单纯的复制过程，容量改变意味着取余操作即键值所对应的的桶改变了。
先说说装载因子吧。

装载因子=已经在哈希表的元素个数/哈希表的容量

很明显装载因子与哈希冲突的可能性成正比，装载因子越大，哈希冲突发生的可能性越大。
以下是HashMap源码中的一些参数。

    /**
     * The default initial capacity - MUST be a power of two.
     */
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
    /*……*/
	/**
     * The load factor used when none specified in constructor.
     */
	static final float DEFAULT_LOAD_FACTOR = 0.75f;
    /**
     * The bin count threshold for using a tree rather than list for a
     * bin.  Bins are converted to trees when adding an element to a
     * bin with at least this many nodes. The value must be greater
     * than 2 and should be at least 8 to mesh with assumptions in
     * tree removal about conversion back to plain bins upon
     * shrinkage.
     */
    static final int TREEIFY_THRESHOLD = 8;

    /**
     * The bin count threshold for untreeifying a (split) bin during a
     * resize operation. Should be less than TREEIFY_THRESHOLD, and at
     * most 6 to mesh with shrinkage detection under removal.
     */
    static final int UNTREEIFY_THRESHOLD = 6;

    /**
     * The smallest table capacity for which bins may be treeified.
     * (Otherwise the table is resized if too many nodes in a bin.)
     * Should be at least 4 * TREEIFY_THRESHOLD to avoid conflicts
     * between resizing and treeification thresholds.
     */
    static final int MIN_TREEIFY_CAPACITY = 64;

HashMap初始化默认容量为16。
树结构与非树结构是针对链表寻址法构建的哈希表，JDK1.8中，对HashMap进行了优化:
当链表长度大于8(TREEIFY_THRESHOLD)时，链表转换为红黑树
当链表长度小于6(UNTREEIFY_THRESHOLD)时，则红黑树又转换成链表。
当进行树结构化时，链表装入的元素数量最小为64(MIN_TREEIFY_CAPACITY)，这是用来避免调整大小和树化阈值之间冲突。

(二)、如何扩容

如前文所说，当装载因子达到一定阈值时(Java默认为0.75)就开始进行扩容操作，并且每次扩容，容量大小为原来的2倍。
前面说到，扩容不是简单的复制，那么如何能够更好的进行扩容机制呢？
你可能会说，那最简单的扩容不就是新申请一个二倍空间的哈希表，然后重新映射不就完了。
理论上是这样，但是当数据量十分巨大时这一过程着实费时间，因此一次性完成数据量的迁移是我们不推荐的。
一次性完成数据量的迁移很难，那可不可以分多次进行数据的搬移呢？
答案是肯定的，采用均摊/分摊的思想进行扩容搬移数据就比较方便啦。
首先，我们先申请相应大小的容量空间。
其次，在每一次插入数据的时候进行搬移：先将所需插入的数据放入到新哈希表中，然后将从旧的哈希表中拿出一个数据放到新的哈希表中。
最后，如果有任何涉及到查询的操作，先对新的哈希表进行查询再到旧的哈希表进行查询。
这样扩容操作效率就高了很多。在加倍扩容机制中，分摊时间复杂度之后，其扩容是时间复杂度为O(1)。

(三)、提问

结合我自己原来所学和他人博客，提出两个小问题。

1. 为什么装载因子设置为0.75？

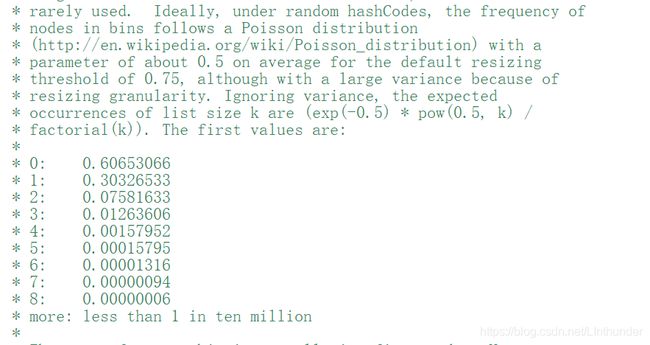
如图，在源码中，有数据研究表明，在随机hashCodes中，桶内的点数频率满足泊松分布，比如桶中有0个点的概率是0.6左右(自我理解如此)。
意思就是有大佬数据员已经给你测试过了，装载因子在0.75的时候，你的现有容量的利用率和需要扩容的频繁度可以较好的协调，不会过早的扩容导致空间和时间的浪费也不会太晚扩容导致哈希冲突发生过多。

2. 为什么要采用容量加倍策略？

这一部分内容，本节采取容量递增与容量倍增对比来说明为何容量加倍策略达到能达到O(1)。
初始容量为0的空表中连续输入n =m*I(n>>2)个元素
a) 容量递增策略：每次追加固定大小的容量I
在第1,I+1,2I+1,3I+1,……次插入扩容
时间：0, I , 2I,……, (m-1)*I
总时间为：I(m-1)m/2=O(n2),均摊时间为O(n)
b) 容量递增策略：每次按照2倍扩容
在第1,2,4,8,……2^m=n 次插入扩容
时间：1, 2, 4,……,2^m=n
总时间为：O(n),均摊时间为O(1)

因此可以看出容量加倍策略的均摊时间复杂度可以降为O(1)。

三、练习实现

下面给出链表寻址法的java代码实现

import java.util.*;

public class LinkingAddressingHashTable<T> {
     
	private static final int DEFAULT_TABLE_SIZE = 101;
	private List<T>[] myLists;
	private int currentSize;
	private int capacity;
	public LinkingAddressingHashTable(){
     
		this(DEFAULT_TABLE_SIZE);
	}
	public LinkingAddressingHashTable(int size){
     
			capacity=nextPrime(size);
			myLists = new LinkedList[nextPrime(capacity)];
			for(int i=0;i<capacity;i++) {
     
				myLists[i] = new LinkedList<>();
			}
	}
	public int nextPrime(int n) {
     
		if(n%2==0)n++;
		for(;!isPrime(n);n+=2);
		return n;
	}
	public boolean isPrime(int n) {
     
		if(n==2||n==3)return true;
		if(n==1||n%2==0)return false;
		for(int i=3;i*i<=n;i+=2){
     
			if(n%i==0) return false;
		}
		return true;
	}
	public void insert(T x) {
     
		List<T> whichList = myLists[myHash(x)];
		if(!whichList.contains(x)) {
     
			whichList.add(x);
			if(++currentSize>capacity) {
     
				reHash();
			}
		}
	}
	public void remove(T x) {
     
		List<T>whichList = myLists[myHash(x)];
		if(whichList.contains(x)) {
     
			whichList.remove(x);
			currentSize--;
		}
	}
	public boolean contains(T x) {
     
		List<T> whichList = myLists[myHash(x)];
		return whichList.contains(x);
	}
	public void makeEmpty() {
     
		for(int i=0;i<capacity;i++) {
     
			myLists[i].clear();
		}
	}
	public int myHash(T x) {
     
		int hashVal = x.hashCode();
		hashVal%=capacity;
		if(hashVal<0) {
     
			hashVal += capacity;
		}
		return hashVal;
	}
	public static int hash(String key,int tableSize) {
     
		int hashVal = 0;
		for(int i=0;i<key.length();i++) {
     
			hashVal = 27*hashVal + key.charAt(i);//hashVal是有符号32位整形
		}
		hashVal%=tableSize;
		if(hashVal<0) hashVal+=tableSize;
		return hashVal;
	}
	public void reHash() {
     
		List<T>[] oldLists = myLists;
		myLists = new List[nextPrime(2*capacity)];
		for(int j=0;j<capacity;j++) {
     
			myLists[j] = new LinkedList();
		}
		currentSize=0;
		for(List<T> list :oldLists) {
     
			for(T item:list) {
     
				insert(item);
			}
		}
	}
	public static void main(String[] args) {
     
		LinkingAddressingHashTable<String> ht = new LinkingAddressingHashTable();
		ht.insert("Zhang San");
		ht.insert("Li Si");
		String x = "Zhang San";
		System.out.print(ht.contains(x));
	}
}

B站同步：数据结构与算法之哈希表