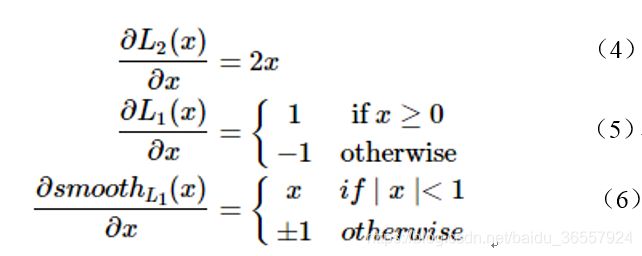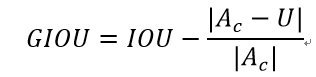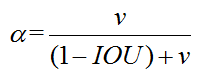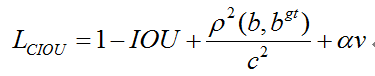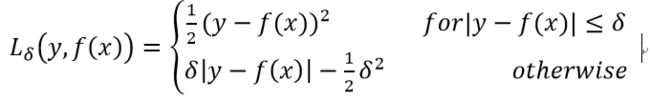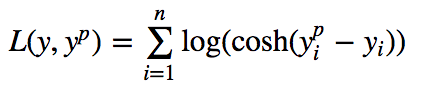目标检测回归损失函数简介

目标检测任务的损失函数由Classificition Loss和Bounding Box Regeression Loss两部分构成。本文介绍目标检测任务中近几年来Bounding Box Regression Loss Function的演进过程，其演进路线：

SmoothL1/IoU/GIoU/DIoU/CIoU Loss

本文按照此路线进行讲解。

1、Smooth L1 Loss

1.1均方误差MSE (L2 Loss)

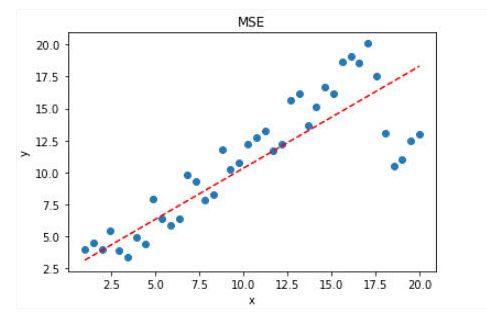
均方误差（Mean Square Error,MSE）是模型预测值f(x)与真实样本值y之间差值平方的平均值，其公式如下

其中，yi和f(xi)分别表示第i个样本的真实值及其对应的预测值，n为样本的个数。忽略下标i，设n=1，以f(x)−y为横轴，MSE的值为纵轴，得到函数的图形如下：

MSE的函数曲线光滑、连续，处处可导，便于使用梯度下降算法，是一种常用的损失函数。而且，随着误差的减小，梯度也在减小，这有利于收敛，即使使用固定的学习速率，也能较快的收敛到最小值。

当y和f(x)也就是真实值和预测值的差值大于1时，会放大误差；而当差值小于1时，则会缩小误差，这是平方运算决定的。MSE对于较大的误差（>1>1）给予较大的惩罚，较小的误差（<1<1）给予较小的惩罚。也就是说，对离群点比较敏感，受其影响较大。

如果样本中存在离群点，MSE会给离群点更高的权重，这就会牺牲其他正常点数据的预测效果，最终降低整体的模型性能。 如下图

可见，使用 MSE 损失函数，受离群点的影响较大，虽然样本中只有 5 个离群点，但是拟合的直线还是比较偏向于离群点。

1.2平均绝对误差MAE（L1 loss）

平均绝对误差（Mean Absolute Error,MAE) 是指模型预测值f(x)和真实值y之间距离的平均值，其公式如下：

MAE=i=1n|fxi-yi|n 

忽略下标i，设n=1，以f(x)−y为横轴，MAE的值为纵轴，得到函数的图形如下：

MAE曲线连续，但是在y−f(x)=0处不可导。而且 MAE 大部分情况下梯度都是相等的，这意味着即使对于小的损失值，其梯度也是大的。这不利于函数的收敛和模型的学习。但是，无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解。相比于MSE，MAE有个优点就是，对于离群点不那么敏感。因为MAE计算的是误差y−f(x)的绝对值，对于任意大小的差值，其惩罚都是固定的。

针对上面带有离群点的数据，MAE的效果要好于MSE。

1.3 MSE和MAE的选择

从梯度的求解以及收敛上，MSE是由于MAE的。MSE处处可导，而且梯度值也是动态变化的，能够快速的收敛；而MAE在0点处不可导，且其梯度保持不变。对于很小的损失值其梯度也很大，在深度学习中，就需要使用变化的学习率，在损失值很小时降低学习率。

对离群（异常）值得处理上，MAE要明显好于MSE。如果离群点（异常值）需要被检测出来，则可以选择MSE作为损失函数；如果离群点只是当做受损的数据处理，则可以选择MAE作为损失函数。

总之，MAE作为损失函数更稳定，并且对离群值不敏感，但是其导数不连续，求解效率低。另外，在深度学习中，收敛较慢。MSE导数求解速度高，但是其对离群值敏感，不过可以将离群值的导数设为0（导数值大于某个阈值）来避免这种情况。

在某些情况下，上述两种损失函数都不能满足需求。例如，若数据中90%的样本对应的目标值为150，剩下10%在0到30之间。那么使用MAE作为损失函数的模型可能会忽视10%的异常点，而对所有样本的预测值都为150。这是因为模型会按中位数来预测。而使用MSE的模型则会给出很多介于0到30的预测值，因为模型会向异常点偏移。

这种情况下，MSE和MAE都是不可取的，简单的办法是对目标变量进行变换，或者使用别的损失函数，例如：Huber，Log-Cosh等。

1.4 Smooth L1 Loss

在Faster R-CNN以及SSD中对边框的回归使用的损失函数都是Smooth L1作为损失函数：

其中，x=f(xi)−yi为真实值和预测值的差值。对比L1 Loss 和L2 Loss，其中x为预测框与groud truth之间的差异：

 上面损失函数对x的导数为：

     

上面导数可以看出：

根据公式（4），当x增大时，L2的损失也增大。 这就导致在训练初期，预测值与 groud truth 差异过于大时，损失函数对预测值的梯度十分大，训练不稳定。

根据公式（5）,L1对x的导数为常数，在训练的后期，预测值与ground truth差异很小时，L1的导数的绝对值仍然为1，而 learning rate 如果不变，损失函数将在稳定值附近波动，难以继续收敛以达到更高精度。

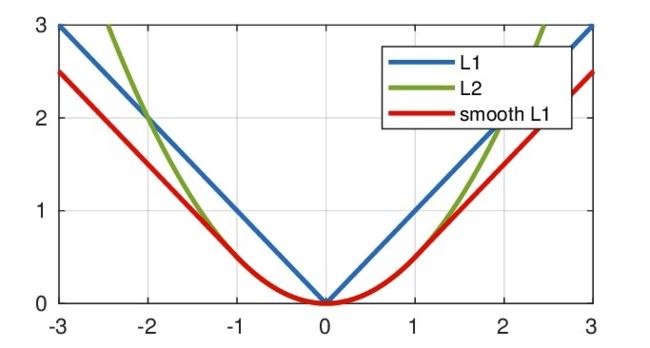
根据公式（6），Smotth L1在x较小时，对x的梯度也会变小。 而当x较大时，对x的梯度的上限为1，也不会太大以至于破坏网络参数。SmoothL1完美的避开了L1和L2作为损失函数的缺陷。L1 Loss ,L2 Loss以及SmoothL1放在一起的函数曲线对比

从上面可以看出，该函数实际上就是一个分段函数，在[-1,1]之间实际上就是L2损失，这样解决了L1的不光滑问题，在[-1,1]区间外，实际上就是L1损失，这样就解决了离群点梯度爆炸的问题

缺点：

上面的三种Loss用于计算目标检测的Bounding Box Loss时，独立的求出4个点的Loss，然后进行相加得到最终的Bounding Box Loss，这种做法的假设是4个点是相互独立的，实际是有一定相关性的

实际评价框检测的指标是使用IOU，这两者是不等价的，多个检测框可能有相同大小的   Loss，但IOU可能差异很大，为了解决这个问题就引入了IOU Loss

2、IOU Loss

2.1优点

IoU就是我们所说的交并比，是目标检测中最常用的指标，在anchor-based的方法中，他的作用不仅用来确定正样本和负样本，还可以用来评价输出框（predict box）和ground-truth的距离。

可以说它可以反映预测检测框与真实检测框的检测效果。

还有一个很好的特性就是尺度不变性，也就是对尺度不敏感（scale invariant）， 在regression任务中，判断predict box和gt的距离最直接的指标就是IoU。(满足非负性；同一性；对称性；三角不等性)

上图中的红色点表示目标检测网络结构中Head部分上的点（i,j），绿色的框表示Ground truth框, 蓝色的框表示Prediction的框，IoU loss的定义如上，先求出2个框的IoU，然后再求个-ln(IoU)，实际很多是直接定义为IoU Loss = 1-IoU

2.2 作为损失函数会出现的问题(缺点)

如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小（重合度）。同时因为loss=0，没有梯度回传，无法进行学习训练。

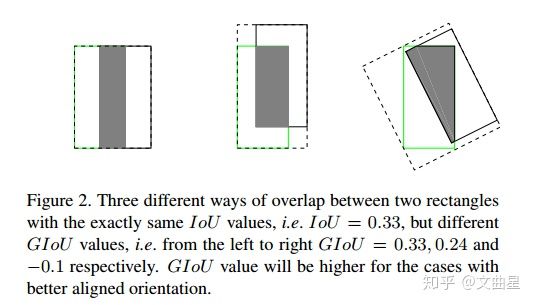
IoU无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

3、GIOU

3.1 简介

在CVPR2019中，一论文提出了GIoU的思想。由于IoU是比值的概念，对目标物体的scale是不敏感的。然而检测任务中的BBox的回归损失(MSE loss, l1-smooth loss等）优化和IoU优化不是完全等价的，而且 Ln 范数对物体的scale也比较敏感，IoU无法直接优化没有重叠的部分。

这篇论文提出可以直接把IoU设为回归的loss。

上面公式的意思是：先计算两个框的最小闭包区域面积Ac  (通俗理解：同时包含了预测框和真实框的最小框的面积)，再计算出IoU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重得到GIoU。

3.2 特性

·与IoU相似，GIoU也是一种距离度量，作为损失函数的话，，满足损失函数的基本要求

·GIoU对scale不敏感

·GIoU是IoU的下界，在两个框无限重合的情况下，IoU=GIoU=1

·IoU取值[0,1]，但GIoU有对称区间，取值范围[-1,1]。在两者重合的时候取最大值1，在两者无交集且无限远的时候取最小值-1，因此GIoU是一个非常好的距离度量指标。

·与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。

总的来说，GIOU包含了IOU所有的优点，同时克服了IOU的不足。

4、DIOU

4.1 优化的方向

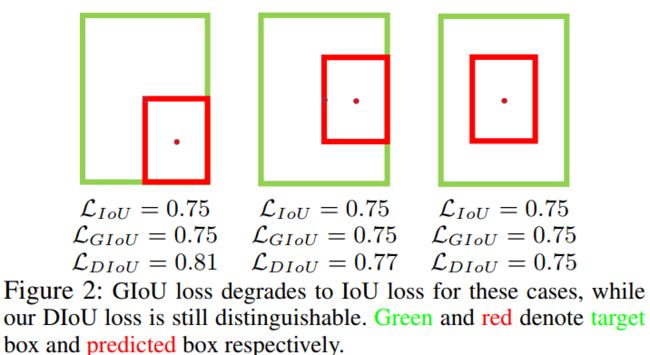
当目标框完全包裹预测框的时候，IoU和GIoU的值都一样，此时GIoU退化为IoU, 无法区分其相对位置关系；此时作者提出的DIoU因为加入了中心点归一化距离，所以可以更好地优化此类问题。

基于IoU和GIoU存在的问题，作者提出了两个问题：
a. 直接最小化anchor框与目标框之间的归一化距离是否可行，以达到更快的收敛速度？
b. 如何使回归在与目标框有重叠甚至包含时更准确、更快？

4.2 DIOU

其中， b、bgt  分别代表了预测框和真实框的中心点，且ρ 代表的是计算两个中心点间的欧式距离。c 代表的是能够同时包含预测框和真实框的最小闭包区域的对角线距离。

优点：

·与GIoU loss类似，DIoU loss（ LDIOU =1-DIOU）在与目标框不重叠时，仍然可以为边界框提供移动方向。

·DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。

·对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快，而GIoU损失几乎退化为IoU损失。

·DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效。

5、CIOU

同时考虑到框回归的3个几何因素（重叠区域，中心点距离，宽高比），基于DIOU，再次提出CIOU，进一步提高收敛速度和回归精度。另外，可以将DIOU结合NMS组成DIOU-NMS，来对预测框进行后处理。其惩罚项如下面公式：

其中α是权重函数

v用来度量长宽比的相似性，定义为 ：，。

完整的 CIoU 损失函数定义：

最后，CIoU loss的梯度类似于DIoU loss，但还要考虑 v的梯度。在长宽在(0,1）情况下， 的值通常很小，会导致梯度爆炸，因此在  实现时替换成1

附：

1.Huber Loss

本质上，Huber损失是绝对误差，只是在误差很小时，就变为平方误差。Huber损失结合了MSE和MAE的优点。但是，Huber损失的问题是可能需要不断调整超参数delta。

2.Log-Cosh损失函数

Log-Cosh是应用于回归任务中的另一种损失函数，它比L2损失更平滑，是预测误差的双曲余弦的对数。

优点：对于较小的x，log(cosh(x))近似等于(x^2)/2，对于较大的x，近似等于abs(x)-log(2)。这意味着‘logcosh’基本类似于均方误差，但不易受到异常点的影响。它具有Huber损失所有的优点，但不同于Huber损失的是，Log-cosh二阶处处可微。

很多机器学习模型，比如XGBoost，使用牛顿法来寻找最好结果，因此需要二阶导数（海塞函数）。对于像XGBoost这样的机器学习框架，二次可微函数更为有利。