Beta分布,二项分布,Dirichlet分布,多项式分布新解
- 阅读说明
- beta分布与二项分布
- 共轭先验
- beta分布与Dirichlet分布
- Dirichlet分布与多项式分布
0. 阅读说明
这四个分布是LDA的基础,很多人废了好久,才把公式推导搞明白。结果发现,这几个的实际意义搞不懂。他们之间的关系也理解不深刻。为此,特做此博文。
此博文并无半点抄袭,完全原创,因此如果你要转载,请注明出处(也好让俺风光风光)
如果看完这篇博文后:
1. 你有了一种恍然大悟的快感
2. 你发现之前读过的资料都是千篇一律抄来抄去却并没有get到痛点。而这篇博文却可以举重若轻,足够深刻
那么希望你看在博主相国大人兢兢业业的份儿上:
哪怕只捐1毛钱,也是一种心意。通过这样的方式,也可以培养整个行业的知识产权意识和服务精神。我可以和您建立更多的联系,并且在相关领域提供给您更多的资料和技术支持。
手机扫一扫,即可:
附:《春天里,我们的拉萨儿童图书馆,需要大家的帮助》
如果你看完之后,觉得并没有想象中的美妙,或者觉得内容有误:
请一定要联系博主:
E-mail:[email protected]
我会给你打赏的!
1. beta分布与二项分布
假设一枚硬币正面朝上的概率为 x ,则反面朝上的概率为 1−x ,现在我投掷100次,30次朝上,于是我会认为, x=0.3 . 现在我再做一组试验,投掷100次29次朝上,这一次我认为 x2=0.29 ,这样,我不断地一组一组做。我就会得到很多 x 。
| x | Group1 | Group2 | Group3 | …… |
|---|---|---|---|---|
| x | 0.3 | 0.31 | 0.28 | …… |
如图所示:
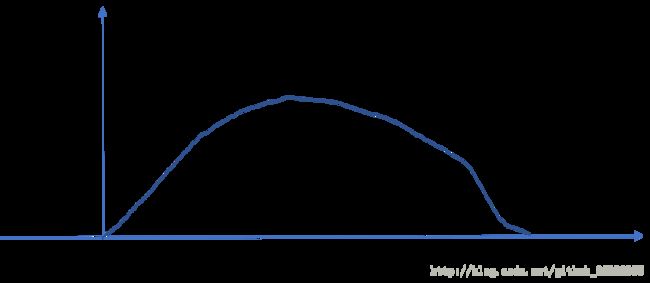
横轴为x的取值。纵轴为x取得某一值出现的次数。这条曲线是一条有零点0,1的曲线,因此根据高中的知识,我们就可以设这条曲线为:
有的宝宝不知道高中知识里哪里有这么个东西。还记得有句话叫做“奇过偶不过”吗?只不过上面这个图当中,我们只关心0-1区间并不关心外面的东西。因此你随意写都可以的。比如,如果一个多项式曲线零点为 x0,x1,x2 那么这个曲线可以写成 (x−x0)α0(x−x1)α1(x−x2)α2 .
同样的,上面那个图可以写成 (x−0)α0(x−1)α1 .于是我说我写成这样也可以:(x−0)α0(1−x)α1你同意不?
你说你不同意,这样曲线不反过来了吗?
我说没问题:
在0-1之间,我写成 (x−0)α(x−1)4 和 (x−0)α(1−x)4 一个意思。
在0-1之间,我写成 (x−0)α(x−1)3 ,图像反过来了,所以我最好应该写成 (x−0)α(1−x)3 。
你说好玩不好玩?
你要是还没明白是怎么回事,那你还是别继续看了。顺道也放弃计算机行业吧。(微笑)
但是,这条曲线还不能说是概率密度函数,因为它在定义域上的积分为必为1.为了保证为1我们可以令曲线与x轴围成的面积为 B(α,β) ,这样我们可以构造一个概率密度函数:
据说有的宝宝连 Γ 函数都不知道,看这里《深入浅出LDA(1)》
我们不妨再来看看二项分布的概率密度公式:
为了让你看懂,我们把这个式子按照 (0.2) 的样子改写一下:
这个改写与之前的并不是完全等价,不过没关系,无非就差几个系数而已。更主要的,我们发现前面的组合操作只不过就是一个系数,仅此而已。因此式子 (0.4) 本质上就是:
与(0.1)不同的是,这里 α,β 是我们感兴趣的,也就是变量。根据二项分布的意义,这 两个变量分别表达正面朝上的次数和反面朝上的次数(当然,并不是绝对的次数,因为我们之前说了,无非就差几个常数而已)。而到了 β 分布里,我们感兴趣的不是朝上朝下的次数了,而是给定了这些次数,让你估计朝上或者朝下的概率。
所以,聪明的你也发现了, β 分布与二项分布的关系是:
二项分布是给定事件概率,让你估计出现的次数。
β 分布是给定了出现的次数,让你估计给定事件的概率。
实际上,这背后的原理还有一个更加深层次的解释:那就是 β 分布是二项分布的共轭先验。
2.共轭先验
为了解释这个概念,我们还是顺着之前的线索,慢慢来:
我们刚刚说过:
- 二项分布是给定事件概率,让你估计出现的次数。
- β 分布是给定了出现的次数,让你估计给定事件的概率。
好了,现在我做了n组实验了,我想知道进行到此时这个概率应该估计为多少比较好呢?
为此,我们使用上面的第2条,也就是 β 分布。
这样一来我们就得到了当前最新的概率估计。但是我们还是要继续做实验的,我们开始做第 n+1 组实验了哦。
现在我们想知道的是,刚才的最新的概率估计到底靠不靠谱呢?我们于是在假定这个概率正确的情况下,来猜一猜我这第 n+1 组实验里,正面朝上应该多少次比较有可能呢?
为此,我们使用上面的第1条,也就是二项分布。
这样一来我们就得到了当前最新的概率估计。但是我们还是要继续做实验的,我们开始做第 n+2 组实验了哦……
这是一个无穷尽的过程,随着你实验的进行,我们最终可以让概率 x 的估计越来越靠谱。
这个迭代的过程,我们刚才的表述中已经无比清晰地向我们展现了如下的关系:
上面这个式子两个 β 分布无非就是参数不同而已,但都是 β 分布。
在贝叶斯理论中,我们把等式左侧的部分叫做后验概率,等式右侧第一项叫做似然,第二项叫做先验概率。贝叶斯理论认为:后验概率 ∝ 似然 × 先验概率。
而在我们的这个场景中,我们发现,这里的后验概率与先验概率遵循同样的分布律。我们把这种情况叫做共轭。即:
此时的先验概率和后验概率互为共轭。
此时的先验概率叫做似然的共轭先验。
以后,只要我们说“A分布是B分布的共轭先验”,你就应该立即明白:A分布 ∝ B分布 × A分布。
接下来,是时候亮出 beta 分布与Dirichlet分布了!
3. beta分布与Dirichlet分布
首先让我们来复习一下之前说过的话:
α,β 两个变量分别表达正面朝上的次数和反面朝上的次数
如果你忘记这个为什么了,点击这里跳转到刚才对应的部分
β 分布的概率密度为:
其中:
Dirichlet分布:
其中:
很多同学连式子 (1.3,1.4) 都看不懂,这就让人尴尬了。
我们如果把 β 分布的密度公式按照Dirichlet的形式改写一下可以变成如下的几种写法:
令 x1=x,x2=1−x,α1=α,α2=β 显然有 x1+x2=1 ,
并且满足: x1+x2=1
这是一个二维的联合概率分布。同时也是Dirichlet在 K=2 时候的情景。
如果我们只考察其中一个变量,那么就可以写成类似于 (1.1) 原来的方程:
或者:
式子 (1.6,1.7) 是单变量,或者说是一维的概率分布,也就是我们原来的 β 分布。这两个图像是互补类似的,因此接下来我们只表示这两个中的一个。
式子 (1.6,1.5) 可以分别表达为下面的示意图:

这个图表达的是公式 (1.6) ,也就是我们说的 β 分布。
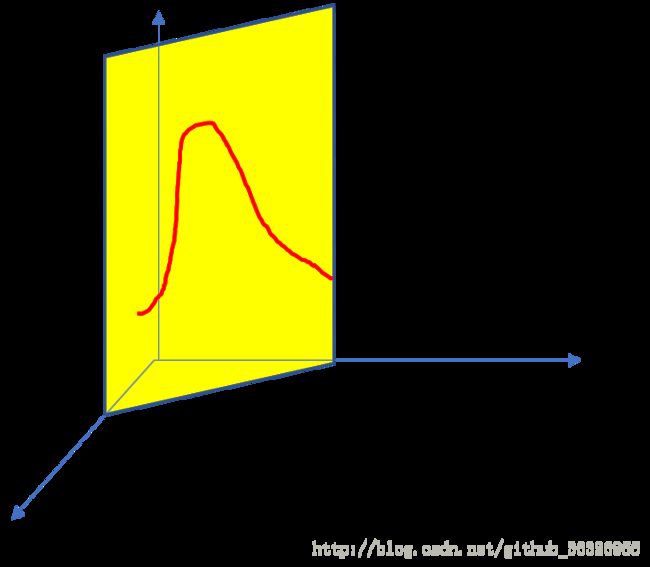
这个图表达的是公式 (1.5) ,也就是我们说的Dirichlet分布在K取2时候的场景。
你会发现: β 分布,可以看作是二维Dirichlet分布在每一个维度上的投影。
那么,如果我们将维度扩充到3维呢?
还是之前投硬币的例子,只是这一次是三个面,不妨叫做骰子。我们每一组试验做了100次,做了无穷多组。这样没组试验都可以得到三个面各自朝上的概率。如下:
| x⃗ =(x1,x2,x3) | Group1 | Group2 | Group3 | …… |
|---|---|---|---|---|
| x1 | 0.3 | 0.31 | 0.28 | …… |
| x2 | 0.25 | 0.22 | 0.27 | …… |
| x3 | 0.45 | 0.47 | 0.45 | …… |
事实上,如果我们只看其中一个维度的话,比如,只看 x1 ,那么我们可以把这里的 x2+x3 看做公式 (1.6) 的 (1−x1) .所以,单独看每一个维度,图像为:

与公式 (1.6) 的示意图一样,也是一个 β 分布。
而如果我们看 (x1,x2,x3) 整体时,我们看的是这三个维度的联合概率分布。也就是我们说的 K=3 时候的Dirichlet分布。如下图所示:

由于这里面仍然有 x1+x2+x3=1 ,而这个东西是三维空间里的一个面(我们把它叫做单纯性),所以有的资料说,Dirichlet分布在K-1维的单纯性中。
我们仍然可以认为: β 分布,可以看作是三维Dirichlet分布在每一个维度上的投影(请注意,我说的是每一个维度,不是每一个二维坐标平面)。
好了,讲到这里,其实Dirichlet的物理意义你也差不多清楚了。接下来,我们来说说多项式分布。聪明的你应该也看出来了,按照我们之前发现 β 分布与二项分布的方法。你现在似乎自己也能发现Dirichlet分布与多项式分布的关系了。
4. Dirichlet分布与多项式分布
什么是多项式分布?
一个多面体有 k 个面,每个面朝上的概率为 p⃗ =(p1,p2,⋯,pk) ,显然有 ∑ki=1pi=1 . 现在抛掷这个多面体 n 次,各个面朝上的次数为 x1,x2,⋯,xk ,显然有 ∑ki=1xi=n . 问这件事情发生的概率是多少?
即:求 p(x1,x2,⋯,xk|p⃗ ,n)
假如我们已经知道了这 n 次结果中,哪些是面1朝上,哪些是面2朝上……,那么这个概率就很简单了: px11px22⋯pxkk
现在的问题是我们不知道哪些是面1朝上,哪些是面2朝上……所以要做一个组合:
为了解决这个问题,我们首先需要从 n 次试验中,找 x1 次试验,将这几次试验结果指定为面1朝上。再从剩下的 n−x1 次试验结果中,找 x2 次试验,将这几次试验结果指定为面2朝上……
于是:
p(x1,x2,⋯,xk|p⃗ ,n)=Cx1nCx2n−x1Cx3n−x1−x2⋯Cxkn−x1−x2−⋯−xk−1px11px22⋯pxkk=n!Πki=1xi!Πki=1pxii
这就是多项式分布的来历。进一步的,二项分布可以认为是二维平面上取得一个点 x⃗ =(x1,x2) 的概率。多项式分布可以认为是k维空间里,取得向量点 x⃗ =(x1,x2,⋯,xk) 的概率。
看到多项式分布这个式子,你会一惊,这家伙跟Dirichlet公公差不都啊。是的,所谓区别无非就是:Dirichlet的超参数是多项式分布的所求变量。多项式的超参数是Dirichlet所求变量。具体是怎么对应的,相信,看过第1节末尾和第2节的你,应该不在话下。
因此同样的,你会明白:Dirichlet分布是多项式分布的共轭先验。
接下来,我来问一个小问题,看看你脑袋瓜子聪不聪明:
Dirichlet分布中的超参数 α⃗ 的物理意义是什么?
如果你不知道答案,请见这里
最后,祝大家天天开心(微笑)
[email protected]
http://blog.csdn.net/github_36326955
I devote myself to dive into typical algorithms on machine learning and deep learning, especially the application in the area of computational personality. My research interests include computational personality, user portrait, online social network, computational society, and ML/DL. In fact you can find the internal connection between these concepts:
In this blog column, I will introduce some typical algorithms about machine learning and deep learning used in OSNs(Online Social Networks), which means we will include NLP, networks community, information diffusion,and individual recommendation system. Apparently, our ultimate target is to dive into user portrait , especially the issues on your personality analysis.
All essays are created by myself, and copyright will be reserved. You can use them for non-commercical intention and if you are so kind to donate me, you can scan the QR code below. All donation will be used to the library of charity for children in Lhasa.
手机扫一扫,即可:
附:《春天里,我们的拉萨儿童图书馆,需要大家的帮助》