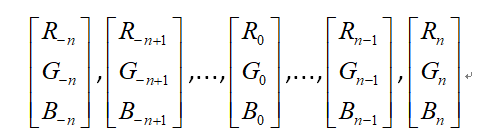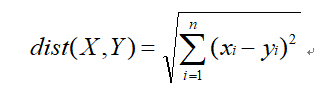图像处理——边缘轮廓拟合算法

前言：
在标注工具上标注时，时常有锯齿形的轮廓需要耗费大量脑细胞来标，因为懒所以思考。。。
需求：简单的点条直线，并调整相应的参数，算法将自动拟合出轮廓曲线，完成此边的标注任务。

算法流程：

1. 读取XML文件的房屋标注框信息，每条边的两个起始点连成一条直线方程。

2. 在此直线方程上取m个等距离的“基点”（m值可调节）。

3. 以每个“基点”为中心，作一条法线，左右各长为n个像素的距离（n值可调节）。

4. 将法线上的每个像素点排成一个列向量：
   

5. 相似度计算——求每两个相邻列向量之间的欧氏距离：
   

6. 欧式距离最大值点即为所求得的“边界位置点”。

7. 将“基点”向“边界位置点”偏移，连接所有新的点，拟合成曲线。

python代码：

from xml.dom.minidom import parse
import re
import cv2
import numpy as np
import math
import time

# 获取直线上‘基点’的坐标
def straightline(p1, p2, m):
    x_spacing = (p2[0] - p1[0]) / (m + 1)
    y_spacing = (p2[1] - p1[1]) / (m + 1)
    return [[p1[0] + i * x_spacing, p1[1] + i * y_spacing] for i in range(1, m + 1)]

# 图像坐标系与数学坐标系变换
def transforme(List,H):
    for i in range(len(List)):
        List[i][1] = H - List[i][1]
    return List

# 过每一个基点，作垂线，
# 设直线方程为Ax+By+C=0，则垂线的斜率k=B/A=(a[0]-a[1])/(b[1]-b[0]);Ci=(a[1]-a[0])P[i][0]+(b[1]-b[0])P[i][1]
# 垂线上距离基点长度为L的点的坐标为（Px+L/(sqrt((1+k)^2)),k*Px+kL/(sqrt((1+k)^2)+Ci)
def verticalline(P, i, L, N, H, d1, d2):
    Pv = []
    d1[1] = H - d1[1]
    d2[1] = H - d2[1]
    if L < N:
        for n in range(1, N + 1):
            k = (d1[0] - d2[0]) / (d2[1] - d1[1])
            Ci = P[i][1] - k * P[i][0]
            Pv.append([round(P[i][0] + L / (math.sqrt((1 + k) ** 2))),
                       round(k * (P[i][0]) + (k * L) / (math.sqrt((1 + k) ** 2)) + Ci)])
            L = n + 1
    return Pv

def detect(K,M,N):
    dom = parse(xmlpath)
    rootdata=dom.documentElement
    image_list=rootdata.getElementsByTagName('image')
    for image in image_list:
        name=image.getAttribute("name")
        H=int(image.getAttribute("height"))
        W=int(image.getAttribute("width"))
        polygon_list = rootdata.getElementsByTagName('polygon')

    img = cv2.imread(name)
    for polygon in polygon_list:
        points_arry = []
        label=polygon.getAttribute("label")
        points_list=polygon.getAttribute("points")
        points_list=re.split(r'[,;]', points_list)
        points_list=list(float(points_list[i]) for i in range(len(points_list)))
        if (len(points_list) % 2 == 0):
            for idx in range(0, len(points_list), 2):
                points_arry.append([points_list[idx], points_list[idx + 1]])
        points_arry.append(points_arry[0])
        print('points_arry:', points_arry)

        #获取第一组端点
        for i in range(0,len(points_arry)-1):
            d1=points_arry[i]
            d2=points_arry[i+1]
            P = straightline(d1, d2, m=M)
            P = transforme(P,H)
            line = [d1]
            for i in range(len(P)):
                Pv = verticalline(P, i, L=1, N=N,H=H,d1=d1,d2=d2)
                Pv = transforme(Pv,H)
                # 获取像素值
                R = []
                G = []
                B = []
                for n in range(len(Pv)):
                    B.append(img[Pv[n][1], Pv[n][0], 0])
                    G.append(img[Pv[n][1], Pv[n][0], 1])
                    R.append(img[Pv[n][1], Pv[n][0], 2])

                # 计算相邻点的相似度
                J = []
                S = []
                for j in range(len(R)):
                    J.append(j + 1)
                    S.append(math.sqrt(R[j] ^ 2 + G[j] ^ 2 + B[j] ^ 2))

                # 返回边界点的索引值
                Index = J[S.index(max(S))]
                # 返回坐标点并可视化
                X0, Y0 = Pv[Index - 1][0], Pv[Index - 1][1]
                line.append([X0, Y0])
            line.append(d2)

            # 将边界点连成一条可视化线
            line = np.array(line, np.int32)
            line = line.reshape((-1, 1, 2))
            cv2.polylines(img, [line], False, (0, 0, 255), 1)
            cv2.imshow("image", img)
    cv2.imwrite("./output/" + str(K) + ".bmp", img)