遗传算法、蚁群算法、粒子群算法解决TSP总结 matlab代码
一、引言
旅行商问题(Traveling Salesman Problem)就是一个经销商从n个城市中的某一城市出发,不重复的走完其余的n-1个城市并回原出发点,求所有可能的路径中路径长度最短的一条。TSP搜索空间随着城市数n的增加而增大,所有的旅程路线组合数为(n-1)!/2。当城市数较大时,TSP难以用遍历的方法找到最短路径。
遗传算法、蚁群算法、粒子群算法都是群优化算法,也就是说我们会在解空间里面同时设置许多个个体然后来组成一个群体来进行搜索寻找最优解。好比我们现在有一个任务,周围有好多个人寻找搜索,而不是一个人寻找搜索。遗传算法里多个个体组成一个种群、蚁群算法的蚂蚁、粒子群算法的粒子都是群优化算法的体现。
本文分别利用以上三种算法来解决31个城市的TSP问题。
二、遗传算法解决TSP问题
遗传算法简介:
遗传算法是一种通过模拟自然进化过程搜索最优解的方法。基本步骤包括:编码、产生初始种群、计算适应度函数值、选择、交叉、变异、产生下一代种群、解码。
适应度函数用来评价个体的性能到底好不好;选择体现进化,更优的个体生存下来进化到下一代可能性比较大;交叉变异保持了样本的多样性,避免算法陷入局部寻优局部求解的误区。
计算适应度函数值->选择->交叉->变异 不停的循环迭代,最后直到满足一定的终止条件。
用来解决TSP问题:
1.编码:在TSP问题中直接用一条路径来对应基因的编码是最简单的表示方式。例如:旅程(3->2->5->8->4->1->6->7)可以直接编码表示为(3 2 5 8 4 1 6 7)
2.适应度函数:计算路径的距离
3.选择算子:轮盘赌法。注意路径越短被选择的概率应该越高,反之路径越长被选择的概率应该越低,因此可以将路径的距离长度取倒数后,再进行轮盘赌选择。
4.交叉算子:基于路径表示的编码方法,要求每个的染色体编码中不允许有重复的基因码,也就是每个城市只能访问一次。因此基本遗传算法的交叉操作不再适用。
本文选用部分匹配交叉法(Partial-MappedCrossover),原理如下:
首先随机产生两个交叉点,定义这两点间的区域为匹配区域,并交换两个父代的匹配区域,如下所示:
父代A:12|3456|789
父代B:54|6921|783
交换后变为:
tempA:12|6921|789
tempB:54|3456|783
对于tempA、tempB中匹配区域以外出现的数码重复,要依据匹配区域内的位置建立映射关系,然后替换,映射关系:
1<->6<->3
2<->5
9<->4
最终结果:
子代A:35|6921|784
子代B:29|3456|781
5.变异算子:在TSP问题中基于二进制编码的变异操作不适用,不能直接将其中一个数码变成另外一个数码(会出现城市的重复)。因此可以随机的在路径抽取两个城市,然后交换他们的位置。这样就实现了个体编码的变异。
%% 1.清空环境变量
clear all;
clc;
%% 2.导入数据
load citys_data.mat; %数据集的变量名为citys
%% 3.计算城市间相互距离
n=size(citys,1);
D=zeros(n,n);
for i=1:n
for j=i+1:n
D(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));
D(j,i)=D(i,j);
end
end
%% 4.初始化参数
m=2000; %种群个数
pop=zeros(m,n); %种群
crospro=0.8; %交叉概率
mutpro=0.1; %变异概率
gen=1; %迭代计数器
genmax=2000; %最大迭代次数
fitness=zeros(m,1); %适应度函数值
Route_best=zeros(genmax,n); %各代最佳路径
Length_best=zeros(genmax,1); %各代最佳路径的长度
Length_ave=zeros(genmax,1); %各代路径的平均长度
%% 5.产生初始种群
% 5.1随机产生初始种群
for i=1:m
pop(i,:)=randperm(n);
end
% 5.2计算初始种群适应度函数值
for i=1:m
for j=1:n-1
fitness(i)=fitness(i) + D(pop(i,j),pop(i,j+1));
end
fitness(i)=fitness(i) + D(pop(i,end),pop(i,1));
end
% 5.3计算最短路径及平均距离
[min_Length,min_index]=min(fitness);
Length_best(1)=min_Length;
Route_best(1,:)=pop(min_index,:);
Length_ave(1)=mean(fitness);
%% 6.迭代寻找最佳路径
while gen<=genmax
% 6.1更新迭代次数
gen=gen+1;
% 6.2选择算子(轮盘赌法)
P=1./fitness;
P=P/sum(P); %计算每一个城市的概率
Pc=cumsum(P); %计算累积概率
popnew=zeros(m,n);
for i=1:m
target_index=find(Pc>=rand);
target=pop(target_index(1),:);
popnew(i,:)=target;
end
% 6.3交叉算子(部分匹配交叉)
for i=1:2:n %两两之间相互交叉
if crospro>rand %判断是否进行交叉
child1path=zeros(1,n);
child2path=zeros(1,n);
setsize=floor(n/2)-1; %匹配区域城市的数量
offset1=randi(setsize); %匹配区域的下边界
offset2=offset1+setsize-1; %匹配区域的上边界
%匹配区域
for j=offset1:offset2
child1path(j)=popnew(i+1,j);
child2path(j)=popnew(i,j);
end
% 非匹配区域
for j=1:offset1-1
child1path(j)=popnew(i,j);
child2path(j)=popnew(i+1,j);
end
for j=offset2+1:n
child1path(j)=popnew(i,j);
child2path(j)=popnew(i+1,j);
end
% 子代1冲突检测
for j=offset1:offset2
if ~ismember(child1path(j),popnew(i,offset1:offset2)) %不在交叉段内
%寻找映射关系
a1=child1path(j);
a2=popnew(i,j);
while ismember(a2,child1path(offset1:offset2))
temp_index=find(popnew(i+1,:)==a2);
a1=a2;
a2=popnew(i,temp_index);
end
%寻找重复数字位置
b1=find(child1path==child1path(j));
if length(b1)>1
if b1(1)>offset2||b1(1)1
if b2(1)>offset2||b2(1)rand %判断是否变异
%随机抽两个数字
y=round(rand(1,2)*(n-1)+1);
%交换位置
temp=popnew(i,y(1));
popnew(i,y(1))=popnew(i,y(2));
popnew(i,y(2))=temp;
end
end
% 6.5计算新一代种群适应度函数值
pop=popnew;
fitness=zeros(m,1);
for i=1:m
for j=1:n-1
fitness(i)=fitness(i) + D(pop(i,j),pop(i,j+1));
end
fitness(i)=fitness(i) + D(pop(i,end),pop(i,1));
end
% 6.6计算最短路径及平均距离
[min_Length,min_index]=min(fitness);
Length_ave(gen)=mean(fitness);
if min_Length 三、蚁群算法解决TSP问题
蚁群算法简介:
蚁群算法灵感来源于蚂蚁在寻找食物过程中的行为。蚂蚁在觅食时会在经过的路径上释放信息素,并且能够感知环境中信息素的含量浓度大小。蚂蚁释放的信息素浓度大小表征了这条路径距离食物的远近:这条路径距离越短,蚂蚁释放的信息素浓度越高。蚂蚁觅食时会以较大概率选择信息素浓度较高的路径,并且在走过这条路径时会释放自己身上的信息素。这样这条路走的蚂蚁越来越多,信息素浓度越高,就会形成一个正反馈。同时路径上信息素的浓度会随着时间的推进而衰减。
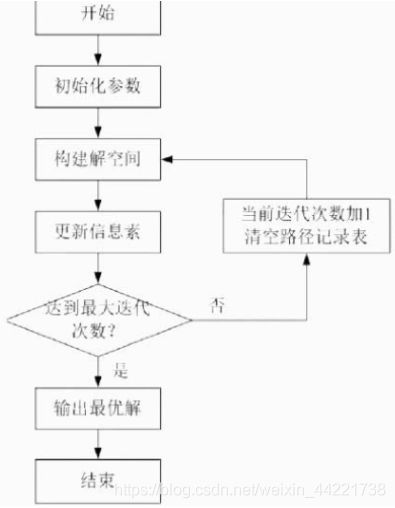
蚁群算法通过 产生路径表->更新信息素->清空路径表 不停的循环迭代来寻找最优解。信息素最大的路径代表最短路径。
用来解决TSP问题:
1.产生路径表:在计算各个城市的访问概率后,用轮盘赌选择下一个访问城市,避免局部最优。
2.更新信息素:对于蚂蚁释放的信息素浓度,本文选用蚁周模型。
%% 1.清空环境变量
clear all;
clc;
%% 2.导入数据
load citys_data.mat; %数据集的变量名为citys
%% 3.计算城市间相互距离
n=size(citys,1);
D=zeros(n,n);
for i=1:n
for j=1:n
if i~=j
D(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));
else
D(i,j)=1e-4;
end
end
end
%% 4.初始化参数
m=50; %蚂蚁数量
alpha=1; %信息素重要程度因子
beta=5; %启发函数重要程度因子
rho=0.1; %信息素挥发因子
Q=1; %常系数
Eta=1./D; %启发函数
Tau=ones(n,n); %信息素矩阵
Table=zeros(m,n); %路径记录表
iter=1; %迭代次数初值
itermax=200; %最大迭代次数
Route_best=zeros(itermax,n); %各代最佳路径
Length_best=zeros(itermax,1); %各代最佳路径的长度
Length_ave=zeros(itermax,1); %各代路径的平均长度
%% 5.迭代寻找最佳路径
while iter<=itermax
% 5.1随机产生各个蚂蚁的起点城市
start=zeros(m,1);
for i=1:m
temp=randperm(n);
start(i,:)=temp(1);
end
Table(:,1)=start;
citys_index=1:n;
% 5.2产生解空间(路径表)
%逐个蚂蚁路径选择
for i=1:m
%逐个城市路径选择
for j=2:n
tabu=Table(i,:); %已访问城市
allow_index=~ismember(citys_index,tabu);
allow=citys_index(allow_index);
P=allow;
% 5.3计算城市间转移概率
for k=1:length(allow)
P(k)=Tau(Table(i,j-1),allow(k))^alpha * Eta(Table(i,j-1),allow(k))^beta;
end
P=P/sum(P);
% 5.4轮盘赌法选择下一个访问城市
Pc=cumsum(P);
target_index=find(Pc>=rand);
target=allow(target_index(1));
Table(i,j)=target;
end
end
% 5.5计算各个蚂蚁的路径距离
Length=zeros(m,1);
for i=1:m
for j=1:n-1
Length(i,1)=Length(i,1)+D(Table(i,j),Table(i,j+1));
end
Length(i,1)=Length(i,1)+D(Table(i,end),Table(i,1));
end
% 5.6计算最短路径及平均距离
if iter==1
[min_Length,min_index]=min(Length);
Length_best(iter)=min_Length;
Route_best(iter,:)=Table(min_index,:);
Length_ave(iter)=mean(Length);
else
[min_Length,min_index]=min(Length);
Length_best(iter)=min(Length_best(iter-1),min_Length);
Length_ave(iter)=mean(Length);
if Length_best(iter-1)>min_Length
Route_best(iter,:)=Table(min_index,:);
else
Route_best(iter,:)=Route_best(iter-1,:);
end
end
% 5.7更新信息素
Delta_Tau=zeros(n,n);
%逐个蚂蚁计算
for i=1:m
%逐个城市计算
for j=1:n-1
Delta_Tau(Table(i,j),Table(i,j+1))=Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,end),Table(i,1))=Delta_Tau(Table(i,end),Table(i,1)) + Q/Length(i);
end
Tau=(1-rho)*Tau+Delta_Tau;
% 5.8迭代次数加1,清空路径表
iter=iter+1;
Table=zeros(m,n);
end
%% 6.结果显示
best_route=Route_best(end,:);
best_length=Length_best(end,:);
disp(['最短距离: ' num2str(best_length)]);
disp(['最短路径: ' num2str(best_route)]);
%% 7.绘图
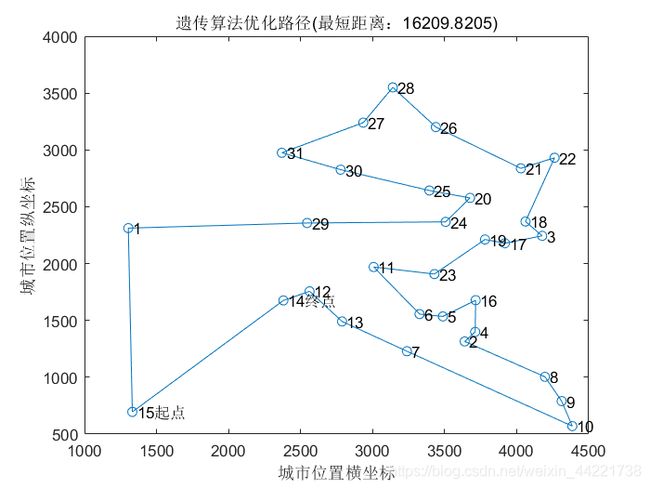
figure(1)
plot([citys(best_route,1);citys(best_route(1),1)],[citys(best_route,2);citys(best_route(1),2)],'o-')
for i=1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(best_route(1),1),citys(best_route(1),2),' 起点');
text(citys(best_route(end),1),citys(best_route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(best_length) ')'])
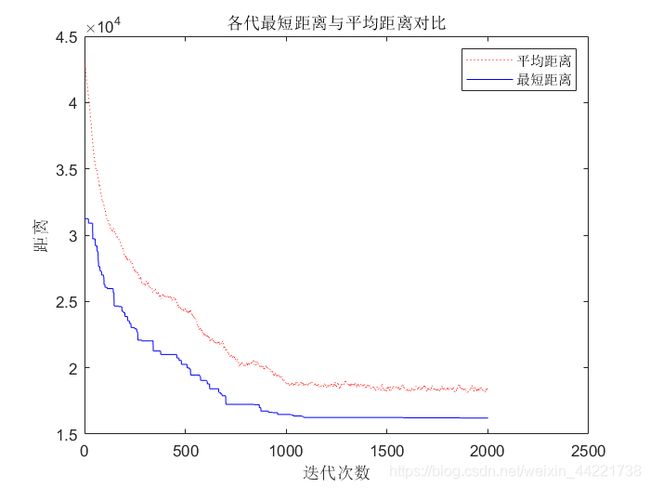
figure(2)
plot(1:itermax,Length_ave,'r:',1:itermax,Length_best,'b-')
legend('平均距离','最短距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
四、粒子群算法解决TSP问题
粒子群算法简介:
粒子群算法源自于对鸟类捕食问题的研究。基本步骤包括:粒子位置和速度初始化、计算适应度函数值、计算个体极值和群体极值、更新速度和位置、更新适应度函数值、更新个体极值和群体极值。
粒子相当于遗传算法里的染色体,他对应的就是解空间里面的一个解。速度是一个矢量,代表的是每个粒子下一次搜索的方向和快慢。个体极值:某一个粒子在多次迭代后它所经历的适应度函数值最好的位置,只是一个粒子的最优。群体极值:所有粒子在多次迭代后它们所经历的适应度函数值最好的位置,是整个群体的最优
更新速度和位置->更新适应度函数值->更新个体极值和群体极值 不停的循环迭代,最后直到满足一定的终止条件。
用来解决TSP问题:
在TSP问题中,粒子的位置可以使用路径来表示,速度如何表示却是一个难题。基本粒子群算法的速度和位置更新公式不再适用,因此本文重新定义了速度和位置的更新公式。
本文重新定义了速度,以及三个运算规则:位置-位置,常数*速度,位置+速度
1.速度定义为交换序列,位置1+速度=位置2定义为位置1通过速度这个交换序列变成位置2,速度中每一个索引对应的数字意为:位置1中索引为该数字的城市与位置1中索引为速度索引的城市对调,例如:
位置1=[5 4 3 2 1]
位置2=[1 2 3 4 5]
位置2[1]=位置1[5]
因此位置1[1]与位置1[5]互换位置,速度[1]=5
交换位置之后:
位置1=[1 4 3 2 5]
位置2=[1 2 3 4 5]
位置2[2]=位置1[4]
因此位置1[2]与位置1[4]互换位置,速度[2]=4
交换位置之后:
位置1=[1 2 3 4 5]
位置2=[1 2 3 4 5]
位置2[3]=位置1[3]
因此位置1[3]与位置1[3]互换位置,速度[3]=3
由此可以推导,速度=[5 4 3 4 5]
位置2-位置1即为速度
2.常数*位置定义为:速度中的每一个值以该常数的概率保留,避免过早陷入局部最优解。
%% 1.清空环境变量
clear all;
clc;
%% 2.导入数据
load citys_data.mat; %数据集的变量名为citys
%% 3.计算城市间相互距离
n=size(citys,1);
D=zeros(n,n);
for i=1:n
for j=i+1:n
D(i,j)=sqrt(sum((citys(i,:)-citys(j,:)).^2));
D(j,i)=D(i,j);
end
end
%% 4.初始化参数
c1=0.1; %个体学习因子
c2=0.075; %社会学习因子
w=1; %惯性因子
m=500; %粒子数量
pop=zeros(m,n); %粒子位置
v=zeros(m,n); %粒子速度
gen=1; %迭代计数器
genmax=2000; %迭代次数
fitness=zeros(m,1); %适应度函数值
Pbest=zeros(m,n); %个体极值路径
Pbest_fitness=zeros(m,1); %个体极值
Gbest=zeros(genmax,n); %群体极值路径
Gbest_fitness=zeros(genmax,1); %群体极值
Length_ave=zeros(genmax,1); %各代路径的平均长度
ws=1; %惯性因子最大值
we=0.8; %惯性因子最小值
%% 5.产生初始粒子
% 5.1随机产生粒子初始位置和速度
for i=1:m
pop(i,:)=randperm(n);
v(i,:)=randperm(n);
end
% 5.2计算粒子适应度函数值
for i=1:m
for j=1:n-1
fitness(i)=fitness(i) + D(pop(i,j),pop(i,j+1));
end
fitness(i)=fitness(i) + D(pop(i,end),pop(i,1));
end
% 5.3计算个体极值和群体极值
Pbest_fitness=fitness;
Pbest=pop;
[Gbest_fitness(1),min_index]=min(fitness);
Gbest(1,:)=pop(min_index,:);
Length_ave(1)=mean(fitness);
%% 6.迭代寻优
while genposition_minus_position.m
function change=position_minus_position(best,pop)
%记录将pop变成best的交换序列
for i=1:size(best,1)
for j=1:size(best,2)
change(i,j)=find(pop(i,:)==best(i,j));
temp=pop(i,j);
pop(i,j)=pop(i,change(i,j));
pop(i,change(i,j))=temp;
end
end
end
constant_times_velocity.m
function change = constant_times_velocity(constant,change)
% 以一定概率保留交换序列
for i=1:size(change,1)
for j=1:size(change,2)
if rand>constant
change(i,j)=0;
end
end
end
end
position_plus_velocity.m
function pop = position_plus_velocity(pop,v)
%利用速度记录的交换序列进行位置修正
for i=1:size(pop,1)
for j=1:size(pop,2)
if v(i,j)~=0
temp=pop(i,j);
pop(i,j)=pop(i,v(i,j));
pop(i,v(i,j))=temp;
end
end
end
end
五、总结
| 遗传算法 | 蚁群算法 | 粒子群算法 | |
|---|---|---|---|
| 优化推进方式 | 选择交叉变异操作 | 信息素浓度的更新 | 速度位置更新 |
| 信息传递 | 种群互相共享信息 | 信息素 | 个体极值和群体极值 |