弱对偶和强队偶的简单证明
目录
-
- 前言
- 弱对偶证明
- 强队偶在几何上的证明
前言
由KKT条件可以通过拉格朗日乘子将一个含不等式和等式的约束条件的最小化问题转为一个拉格朗日函数。
含 约 束 的 原 问 题 = { min x f ( x ) x ∈ R n m i ( x ) ≤ 0 i = 1 , 2... , m n j ( x ) = 0 j = 1 , 2 , . . . , n (1) 含约束的原问题=\begin{cases} \min_{x} f(x)& x\in\ R^n \\ m_i(x) \leq 0 & i = 1,2...,m \\ n_j(x) = 0 & j = 1,2,...,n \end{cases} \tag{1} 含约束的原问题=⎩⎪⎨⎪⎧minxf(x)mi(x)≤0nj(x)=0x∈ Rni=1,2...,mj=1,2,...,n(1)
拉 格 朗 日 函 数 = { min x max λ , η L ( x , λ , η ) = f ( x ) + ∑ i = 0 m λ i m i + ∑ j = 0 n η j n j λ i ≥ 0 λ i m i = 0 (2) 拉格朗日函数=\begin{cases} \min_{x}\max_{\lambda,\eta} L(x,\lambda,\eta) = f(x) + \sum_{i=0}^m\lambda_im_i + \sum_{j=0}^n\eta_j n_j \\ \lambda_i \geq 0 \\ \lambda_i m_i = 0 \end{cases} \tag{2} 拉格朗日函数=⎩⎪⎨⎪⎧minxmaxλ,ηL(x,λ,η)=f(x)+∑i=0mλimi+∑j=0nηjnjλi≥0λimi=0(2)
弱对偶证明
首先将拉格朗日函数转为其对偶问题。
对 偶 问 题 = { max λ , η min x L ( x , λ , η ) λ i ≥ 0 λ i m i = 0 (3) 对偶问题=\begin{cases} \max_{\lambda,\eta}\min_{x} L(x,\lambda,\eta) \\ \lambda_i \geq 0 \\ \lambda_i m_i = 0 \end{cases} \tag{3} 对偶问题=⎩⎪⎨⎪⎧maxλ,ηminxL(x,λ,η)λi≥0λimi=0(3)
弱对偶定义:(对偶问题 ≤ \leq ≤ 原问题)
max λ , η min x L ( x , λ , η ) ≤ min x max λ , η L ( x , λ , η ) \max_{\lambda,\eta}\min_{x} L(x,\lambda,\eta) \leq \min_{x}\max_{\lambda,\eta} L(x,\lambda,\eta) λ,ηmaxxminL(x,λ,η)≤xminλ,ηmaxL(x,λ,η)
- 证明
max λ , η min x L ( x , λ , η ) ≤ min x max λ , η L ( x , λ , η ) \max_{\lambda,\eta}\min_{x} L(x,\lambda,\eta) \leq \min_{x}\max_{\lambda,\eta} L(x,\lambda,\eta) λ,ηmaxxminL(x,λ,η)≤xminλ,ηmaxL(x,λ,η)
∵ min x L ⏟ A ( λ , η ) ≤ L ≤ max λ , η L ⏟ B ( x ) \because \underbrace{\min_{x} L}_{A(\lambda,\eta)} \leq L \leq \underbrace{\max_{\lambda,\eta} L}_{B(x)} ∵A(λ,η) xminL≤L≤B(x) λ,ηmaxL
∴ A ( λ , η ) ≤ B ( x ) \therefore A(\lambda,\eta) \leq B(x) ∴A(λ,η)≤B(x)
∴ max λ , η A ( λ , η ) ≤ min x B ( x ) \therefore \max_{\lambda,\eta}A(\lambda,\eta) \leq \min_{x} B(x) ∴λ,ηmaxA(λ,η)≤xminB(x)
故 可 得 : max λ , η min x L ( x , λ , η ) ≤ min x max λ , η L ( x , λ , η ) 故可得:\max_{\lambda,\eta}\min_{x} L(x,\lambda,\eta) \leq \min_{x}\max_{\lambda,\eta} L(x,\lambda,\eta) 故可得:λ,ηmaxxminL(x,λ,η)≤xminλ,ηmaxL(x,λ,η)
强队偶在几何上的证明
强队偶定义:((对偶问题 = 原问题))
max λ , η min x L ( x , λ , η ) = min x max λ , η L ( x , λ , η ) \max_{\lambda,\eta}\min_{x} L(x,\lambda,\eta) =\min_{x}\max_{\lambda,\eta} L(x,\lambda,\eta) λ,ηmaxxminL(x,λ,η)=xminλ,ηmaxL(x,λ,η)
- 证明
为了简化问题,将原问题进行简化。
原 问 题 = { min x f ( x ) x ∈ R n m 1 ( x ) ≤ 0 x ∈ M m (4) 原问题=\begin{cases} \min_{x} f(x)& x\in\ R^n \\ m_1(x) \leq 0 & x\in M^m \end{cases} \tag{4} 原问题={ minxf(x)m1(x)≤0x∈ Rnx∈Mm(4)
对 偶 问 题 = { max λ min x L ( x , λ ) λ ≥ 0 λ m 1 = 0 (5) 对偶问题=\begin{cases} \max_{\lambda}\min_{x} L(x,\lambda) \\ \lambda \geq 0 \\ \lambda m_1 = 0 \end{cases} \tag{5} 对偶问题=⎩⎪⎨⎪⎧maxλminxL(x,λ)λ≥0λm1=0(5)
设原问题最优解P* = min f ( x ) \min_{}f(x) minf(x)
对偶问题的最优解D* = max λ \max_{\lambda} maxλ min x \min_{x} minxL(x, λ \lambda λ)
令原问题的定义域为D = dom f ⋂ \bigcap ⋂ dom m1
设m1(x) = u,f(x) = t,
则下图的区域设为G = {(u,t)| x ∈ \in ∈ D}
所以,P* = inf { t | (u,t) ∈ \in ∈ G ∩ \cap ∩ u ≤ \leq ≤ 0} ,即在下图的阴影部分取t轴上的最小值。
同理,D* = max λ \max_{\lambda} maxλ min x \min_{x} minxL(x, λ \lambda λ) = max λ \max_{\lambda} maxλ min x \min_{x} minx (t+ λ \lambda λu)
设g( λ \lambda λ) = min x \min_{x} minx( λ \lambda λ)
在 λ \lambda λ固定的情况下,t+ λ \lambda λu = 0为下图过原点的一条直线,通过向上平移,在刚好经过区域G时,可得最小的g( λ \lambda λ),如下图的黄线部分。
但当 λ \lambda λ可以改变时,当直线同时可区域G最下端两个点相切时,可取最小的值D*,如下图的红线部分。
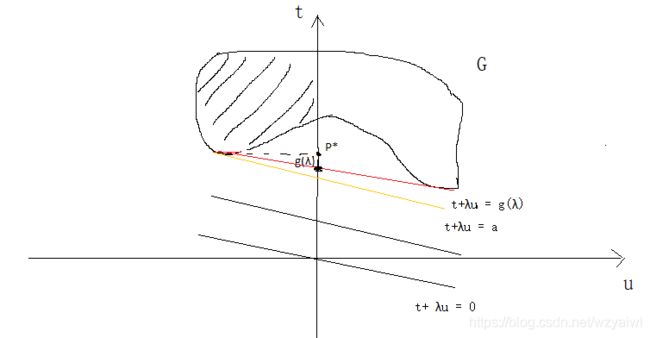
上图可知,对于凹形的边界,符合弱对偶性, P* > max λ \max_{\lambda} maxλg( λ \lambda λ) ⟹ \Longrightarrow ⟹ 原问题 > 对偶问题。
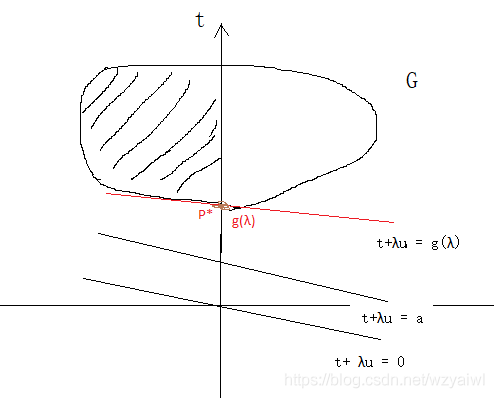
上图可知,对于凸形的边界,符合强对偶性,P* = max λ \max_{\lambda} maxλg( λ \lambda λ) ⟹ \Longrightarrow ⟹ 原问题 = 对偶问题。