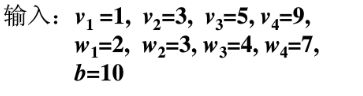【算法】动态规划 背包问题 python

博主根据老师讲义，自己手撸代码，若有错误，多谢指出。直接上代码

目录

0 讲义 

问题定义    子问题划分（ 备忘录函数   标记函数）

举个栗子

1 代码

1.1 code：背包问题

1.2 code：追踪解

1.3 code：主函数

---

0 讲义 

0.1 问题定义

建模

0.2 子问题划分

备忘录函数

标记函数

0.3 举个栗子

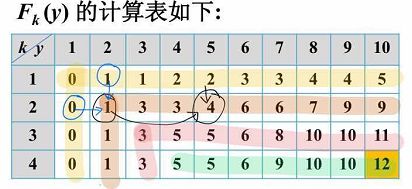
备忘录函数的计算顺序可以是这样的：第一行→第一列→第二行→第二列→。。。→第4行

就像博主画的轨迹一样

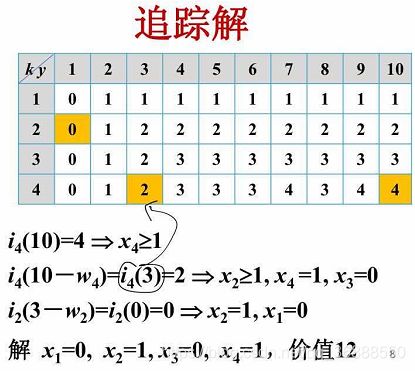
追踪解的过程 附赠一个伪代码 虽然感觉不是很难

1 直接上代码

1.1 code：背包问题

import numpy as np

"""
背包物品上限n个，重量上限为b
第i个物品的重量、价值分别为w[i],v[i]
子问题的界定：对前k个物品进行分析，背包重量不超过y
注意，为了使物品序号都从1开始，初始化的时候会多一行一列
"""
# def bag(w=[0,2,3,4,7], v=[0,1,3,5,9], n=4, b=10, k=1, y=1, memo=None, seq=None):
def bag(w, v, n, b, k=1, y=1, memo=None, seq=None):
    if k==1 and y==1:  
        
        # 最开始的时候，初始化数组
        memo = np.zeros([n+1,b+1], dtype=int)
        seq = np.zeros([n+1,b+1], dtype=int)
        
        for j in range(y,b+1):  # 遍历第一行，此时, 重量上限为j, 物品都是第1个
            memo[k,j] = math.floor(j / w[k]) * v[k]
            if memo[k,j] != 0 : seq[k,j] = 1
                
        for i in range(k,n+1):  # 遍历第一列, 此时,重量上限都为1, 物品都是第i个
            memo[i,y] = math.floor( 1 / w[i] ) * v[i]
            if memo[i,y] != 0 : seq[i,y] = i
                
    else:  # 其他情况，memo[i,j] = max(memo[k-1, y], memo[k, y-w[i] + v[i]])
        
        for j in range(y,b+1):  # 先横着遍历
            p = memo[k-1,j]
            q = memo[k, j-w[k]] + v[k] if j-w[k] >=0 else 0
            if p > q: 
                memo[k,j] = p
                seq[k,j]  = seq[k-1, y]
            else:
                memo[k,j] = q
                seq[k,j]  = k if q!=0 else 0
        
        for i in range(k,n+1):  # 竖着遍历
            p = memo[i-1,y]
            q = memo[i, y-w[i]] + v[i] if y-w[i] >=0 else 0
            
            if p > q: 
                memo[i,y] = p
                seq[i,y]  = seq[i-1, y]
            else:
                memo[i,y] = q
                seq[i,y]  = k if q!=0 else 0
    
    # 遍历下一个
    if k < n and y < b: bag(w,v,n,b,k+1,y+1,memo,seq)
    return memo,seq
        

"""
meno = 
[[ 0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  1  1  2  2  3  3  4  4  5]
 [ 0  0  1  3  3  4  6  6  7  9  9]
 [ 0  0  1  3  5  5  6  8 10 10 11]
 [ 0  0  1  3  5  5  6  9 10 10 12]]

seq = 
[[0 0 0 0 0 0 0 0 0 0 0]
 [0 0 1 1 1 1 1 1 1 1 1]
 [0 0 1 2 2 2 2 2 2 2 2]
 [0 0 1 2 3 3 3 3 3 3 3]
 [0 0 1 2 3 3 3 4 3 4 4]]
"""

 

1.2 code：追踪解

def trace(seq, w, k=0, y=0, ans=[]):
    if len(ans)==0:  # 初始化答案数组，最开始的k，y在seq的最后一行、最后一列
        ans = np.zeros(len(seq), dtype=int)  # 注意，开头多了一个数0
        k,y = np.shape(seq) - np.array([1,1])
        
    next_k = seq[k, y]
    next_y = y - w[next_k]
    ans[next_k] += 1
    
    if next_k != 0: 
        trace(seq, w, next_k, next_y, ans)
        
    return ans[1:]  # 初始化的时候多了一位，返回要去掉一位

"""
ans = array([0, 1, 0, 1])
"""

1.3 code：主函数

# 主函数
b = eval(input('请输入购物车容量：'))
n = eval(input('请输入物品种类个数：'))
w, v = [0], [0]  # 物品的序号是从1开始，所以数组开头要加个0
w.extend(eval(input('请输入物品重量：')))
v.extend(eval(input('请输入物品价值：')))

m,s = bag(w, v, n, b)
ans = trace(s,w=[0,2,3,4,7])

# 输出解
string = ''
for i in range(n):
    string += 'X%d=%d,'%(i+1, ans[i])
print('解 %s 价值%d'%(string, m[-1,-1]))

"""
请输入购物车容量：10
请输入物品种类个数：4
请输入物品重量：2,3,4,7
请输入物品价值：1,3,5,9
解 X1=0,X2=1,X3=0,X4=1, 价值12
"""