【图解算法】栈和队列的构造和相互实现、最小栈

算法题这里不会讲解基础概念，如果连栈和队列都不清楚的同学们，可能需要自己先去了解下。如果以前学过但是忘了的，是可以用本篇文章来回忆相关细节的。这篇文章会放代码，代码能力一般的同学建议在电脑上完成阅读。

问题描述

1. 如何用数组实现固定长度的栈和队列？【基础】
2. 如何只用队列实现一个栈？【有一定技巧】
3. 如何只用栈实现一个队列？【有一定技巧】
4. 如何实现一个最小栈，即一个具备返回最小值函数的栈？【有一定难度和技巧性】

使用数组实现固定长度的栈

对于大多数人而言，这题就是送分题，当然，在面试场景下，如何确保又快又准地完成这道题目，就需要考验我们的coding能力了，对于自认为基础较好的同学，建议花一两分钟思考下push和pop函数的设计，然后再往下看进行验证；对于自认基础一般的同学，建议花5-10 分钟写一下这个代码，写完再进行验证；对于没有学过的同学，建议看看思路即可。

废话少说，我们都知道栈的特性：先进后出，后进先出（FILO），因此，关键考虑点就是push函数和pop函数如何设计。

首先我们构建一个栈类：

class Stack {
     
    vector<int> arr;
    int size; // 栈当前长度
public:
    Stack(int len) {
      // 构造函数，len 为初始化大小
        arr.resize(len); // 给数组分配空间，调用 arr.size() 可以得到这个 len
        size = 0;
    }
};

push函数，首当其冲的就是边界考虑，如果栈已经满了，我们不能继续加到数组中，否则会溢出；至于push进去，我们使用size++非常方便和简洁，因为size一开始是0，而第一个位置的下标也是0，当我们推入一个数字后，size又应该增加一。

void push(int num) {
     
    if (size == arr.size()) {
      // 边界，面试时容易忽略
        throw "the stack is full!";
    }
    arr[size++] = num;
}

pop函数，依然要考虑边界，如果栈已经是空的了，那么就不能继续推出；至于被推出的数据我们并不需要做特殊的处理，实际上我们只需要标记好栈的当前长度即可。

int pop() {
     
    if (size == 0) {
      // 如果栈为空，则不再推出
        throw "the stack is empty!";
    }
    return arr[--size];
}

另外，这里我们模仿了java中的栈的弹出写法，不像cpp中为无返回值，我们会返回被推出的数的值。

使用数组实现固定长度的队列

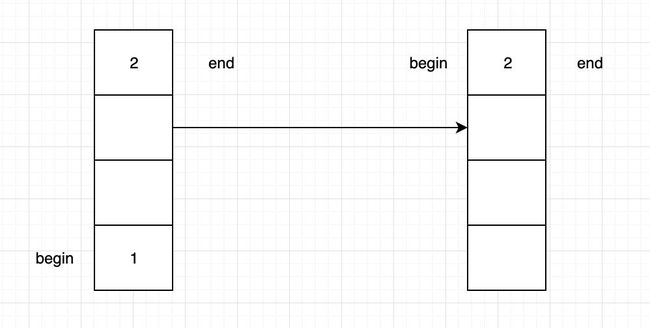
所谓队列，即先进先出，后进后出（FIFO）的结构。有了前面写栈的经验，这里就不多说了，重点依然是边界，当然队列我们需要充分利用数组的空间，因此需要两个变量，分别记录开始和结尾。

构造队列类：

class Queue {
     
    vector<int> arr;
    int size;  // 队列当前长度
    int begin; // 起始位置下标
    int end; 	 // 结束位置下标
public:
    Queue(int size) {
     
        arr.resize(size);
        size = 0;
        begin = 0;
        end = 0;
    }
};

push函数：

void push(int num) {
     
    size++;
    arr[end] = num;
    end = (size == arr.size() - 1) ? 0 : end + 1;
}

要注意，当end到达数组的末尾，但当前长度 < 数组大小时，说明数组前部分还有空位（即begin > 0）。

如果size和arr.size() - 1相等，说明当前队列已经到达末尾了，end需要回到开头；否则，end向后移即可。

pop函数：

int pop() {
     
    if (size == 0) {
      // 队列已经空了，不能再弹出了。
	      throw "the queue is empty!!";
        return NULL;
    }
    int tmp = begin;
    size--;
    begin = (begin == arr.size() - 1) ? 0 : begin + 1;
    return arr[tmp];
}

关于这句begin = (begin == arr.size() - 1) ? 0 : begin + 1;，如果begin到达了队列的末尾，此时pop弹出，那么begin需要回到数组开头，否则，begin自增即可。

如何只用队列实现一个栈

只用队列实现栈，没有接触过这道题的同学，咋一看会比较懵逼，但实际上往往是忽略了队列的个数。事实上我们可以使用两个队列来实现。

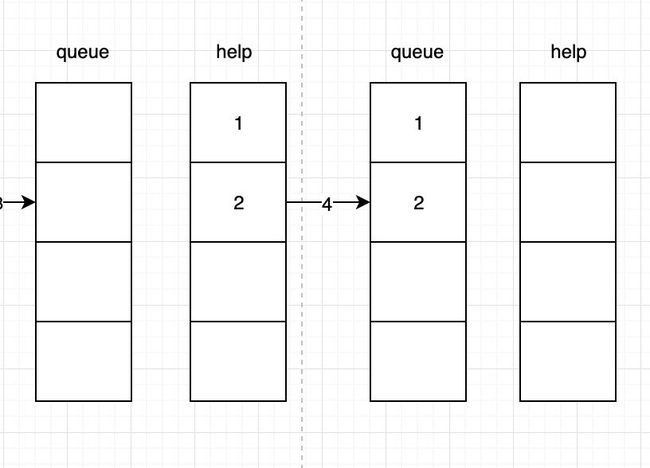
如下图所示，我们使用两个队列queue和help来实现这个栈：

首先我们先在queue˙中放入三个数，注意这里使用的是队列，此时我们想要弹出3，而队列只能取最前面的数，因此我们要另辟蹊径：

1. queue.size() > 1，将queue的队首弹出并压入help中；
2. queue.size() > 1，将queue的队首弹出并压入help中；
3. queue.size() == 1，暂存当前队首（栈顶元素），这是我们待会要返回出去的数；

4. 也是最关键的一步，我们将queue和help交换：
5. 返回前面暂存的栈顶元素即可。

至此，我们相当于完成了pop函数，而push函数，实际上判断一下边界（如果有的话），存入queue中即可。

代码实现：

class Stack{
     
    queue<int> my_queue;	// 数据队列
    queue<int> help;			// 辅助队列
public:
    void push(int num) {
      // 这里我没有使用固定数组，因此无需判断边界
        my_queue.push(num);
    }
  
    int pop() {
     
        if (my_queue.empty()){
      // 判断边界
            cout<<"the stack is empty!"<<endl;
            return NULL;
        }
        while (my_queue.size() > 1) {
     
            help.push(my_queue.front());
            my_queue.pop();
        }
        int res = my_queue.front(); // 暂存栈顶元素
        my_queue.pop();
        swap(); // 交换两个队列
        return res;
    }

    void swap() {
     
        queue<int> temp = my_queue;
        my_queue = help;
        help = temp;
    }
};

如何只用栈实现一个队列

有了前面用队列实现栈的经验，接下来考虑用栈实现队列也会更加简单。同样的，我们使用两个栈来实现队列。

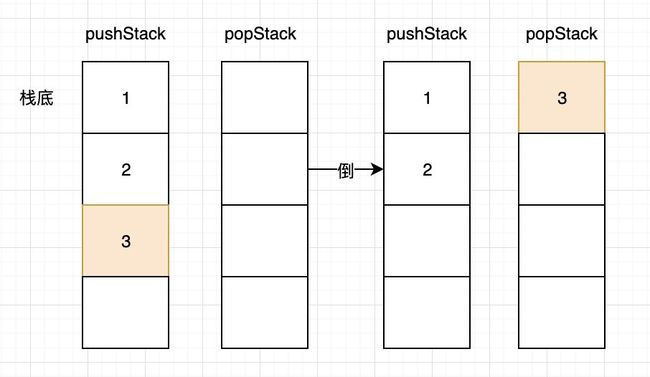
队列是先进先出，而栈是后进先出，那么我们怎么用栈实现呢？脑子灵光的同学们可能已经想到了：把一个栈倒入另一个栈里：

关键部分来了，我们只需每次倒栈的时候将pushStack中的数据全部倒入popStack，且popStack为空时才进行倒栈操作即可。（大家可以思考一下为什么？）

倒栈操作实现：

void pushToPop() {
     
   while(!push_stack.empty()) {
     
     pop_stack.push(push_stack.top());
     push_stack.pop();
   }
}

其他部分代码：

class Queue{
     
    stack<int> push_stack;
    stack<int> pop_stack;

    void pushToPop() {
     ...}

public:
    void push(int num) {
     
        push_stack.push(num);
    }

    int pop() {
     
        if (pop_stack.empty()) {
     
            pushToPop();
        }
        if(pop_stack.empty()) {
     
            cout <<"the queue is empty!" << endl;
        }
        int top = pop_stack.top();
        pop_stack.pop();
        return top;
    }
};

如何实现一个最小栈，即一个具备返回最小值函数的栈？

这一题就比较有意思了，我们如何实现一个栈，能随时的获取这个栈里面的最小值呢？可能有朋友会不假思索的说这很简单，用一个变量来存最小值就好了。嘿，这就忘了一点了，栈是会变化的，假如当前栈顶是最小值，你弹出之后，去哪里找次小值呢？

大部分同学在此处就会懵逼了，那应该怎么做呢？

其实很简单，我们再拿一个栈来存储最小值即可：即我们有一个dataStack和一个minStack，前者存储数据，后者存储最小值；那么最小值该怎么存呢？

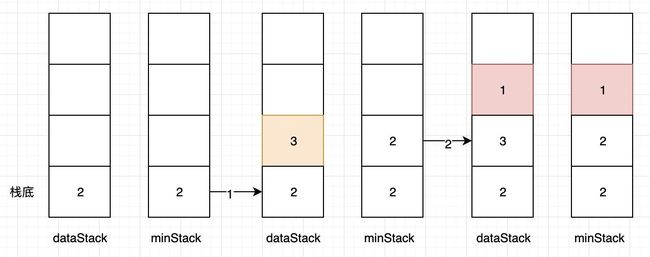
和数据栈并行的存，也就是说最小栈的长度和数据栈的长度一致，每个数据代表同等长度下的栈的最小值。

画个图你们就明白了：

0. 当我们一开始压入2时，因为此时minStack为空，所以直接压入即可；
1. 当我们压入3的时候，此时3 > minStack.top()即3 > 2，因此，我们压入当前的最小值2；
2. 当我们压入1的时候，此时1 < minStack.top()即1 < 2，因此，我们压入新的最小值1。
3. 弹栈操作则更加简单，minStack只需跟随dataStack进行弹栈即可。

代码实现如下：

class MinStack {
     
    stack<int> data_stack; // 数据栈
    stack<int> min_stack;  // 最小栈
public:
    void push(int num) {
     
        if (min_stack.empty()) {
      // minStack为空，直接推入
            min_stack.push(num);
        } else if (min_stack.top() < num) {
      // 新推入的值大于最小值，则依然推入最小值
            min_stack.push(min_stack.top());
        } else {
      // 否则推入新的最小值
            min_stack.push(num);
        }
        // 数据栈不论什么情况下都直接推入数据即可
        data_stack.push(num);
    }

    int top() {
     
        return data_stack.top();
    }

    int pop() {
     
        int top = data_stack.top();
        min_stack.pop();
        data_stack.pop();
        return top;
    }

    int getMin() {
      // 此处使用STL实现，边界就不用自行处理了，当然面试时可以加上
        return min_stack.top();
    }
};

推荐阅读

【面试必会】全网最具深度的三次握手、四次挥手讲解

【面试必会】一文搞懂 TopK 问题及其变种