cht讲算法——数论——欧几里得算法与拓展欧几里得算法（1）

欧几里得算法与拓展欧几里得算法（1）——数论中的beatsaber

哈罗大家好我是cht。

今天正式开死数论部分的讲解！

一、欧几里得算法的思路

众所周知，beatsaber是一个yxc巨佬喜爱的VR游戏。
（大佬：烂人你怎么又开始扯游戏了
好了好了一会大家就知道了。

1-1欧几里得算法用来解决什么东西

其实朴素欧几里得算法最大的用途就是：

求最大公因最小公倍数。

这里要先介绍一点点小东西：
$\frac{a\times b}{(a,b)}=[a,b]$
简明一点，就是：
$a\times b÷a与b的最大公约数=a与b的最小公倍数$
证明如下：
$$\begin{gathered} 令d=(A,B); \\ 则a=\frac{A}{d} \\ b=\frac{B}{d} \\ (a,b)=1 \\ 可列出短除： \\ d|A,B \\ \cdot \cdot —— \\ \cdot \cdot a,b \\ (Markdown并没有短除功能 \\ 此时把A与B分解质因数： \\ A=p_1^{{\alpha }_1}\times p_2^{{\alpha }_2}\times p_3^{{\alpha }_3}\times \cdots \\ B=q_1^{{\beta }_1}\times q_2^{{\beta }_2}\times q_3^{{\beta }_3}\times \cdots \\ d必然包含在其中一个因子里， \\ 不妨设: \\ d=p_x^{{\alpha }_x}=q_y^{{\beta }_y} \\ \because d=p_x^{{\alpha }_x}=q_y^{{\beta }_y} \\ \therefore a=A÷p_x^{{\alpha }_x},b=B÷q_y^{{\beta }_y} \\ 所以可以推出： \\ [A,B]=\frac{a\times b}{(a,b)} \end{gathered}$$

---

1-2欧几里得算法的证明

好我们继续。
朴素欧几里得算法是如何求出来的呢？
请看下面的流程图。

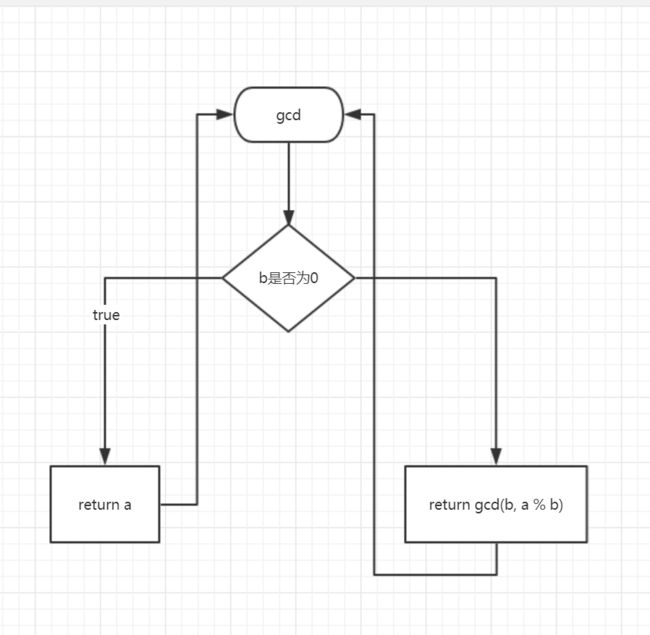
那我们如何理解这个return gcd(b, a % b)呢？
这就是小学奥数中的辗转相除法了。
具体证明可以参考百度百科，这里提供一版y总的证明。
$$\begin{gathered} 令d=gcd(a,b); \\ \because d=gcd(a,b); \\ \therefore \\ d\mathrm{m}\mathrm{o}\mathrm{d}a\equiv 0 \\ d\mathrm{m}\mathrm{o}\mathrm{d}b\equiv 0 \\ \therefore d\mathrm{m}\mathrm{o}\mathrm{d}a\times x+b\times y\equiv 0 \\ \because d\mathrm{m}\mathrm{o}\mathrm{d}a\times x+b\times y\equiv 0 \\ \therefore gcd(a,b)=gcd(b,a-c\times b); \\ \because d\mathrm{m}\mathrm{o}\mathrm{d}a\equiv 0 \\ \therefore gcd(a,b)=gcd(b,a\mathrm{m}\mathrm{o}\mathrm{d}b); \\ 证毕。 \end{gathered}$$

---

二、欧几里得算法的实现

其实证明一套套，代码就3行。

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

……

---

三、套入题目

题目在此
给定n对正整数ai,bi，请你求出每对数的最大公约数。

输入格式
第一行包含整数n。

接下来n行，每行包含一个整数对ai,bi。

输出格式
输出共n行，每行输出一个整数对的最大公约数。

数据范围
$$\begin{gathered} 1\le n\le 10^5, \\ 1\le a[i],b[i]\le 2\ast 10^9 \end{gathered}$$
输入样例：

2
3 6
4 6

输出样例：

3
2

本题需要加上输入输出。
按照顺序输出gcd就行了。

#include
using namespace std;
int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}
int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        int a, b;
        cin >> a >> b;
        cout << gcd(a, b) <

这是我的全部分享

bye~

不过最后还是需要说一句话：

gcd的过程不像 beat saber 吗