ST表——杨子曰数据结构
ST表——杨子曰数据结构
今天我们来曰一种O(1)查询的数据结构——ST表
它,就是RMQ问题的克星!
给你一个数列,对于询问[l,r],输出区间[l,r]内的最大值(你喜欢最小值也可以啦!)
这……我用线段树O(log n)(搞一搞不久好了吗?
不好!!!我们是追求速度的人,由于它没有更新操作,我们可以做到O(1)查询
我们的ST表闪亮登场!!
(在下面的东西前你也可以先阅读一下:谈谈最近公共祖先(LCA)——杨子曰算法,有助于理解)
黑喂狗:
ST表最最重要的思想就是——倍增
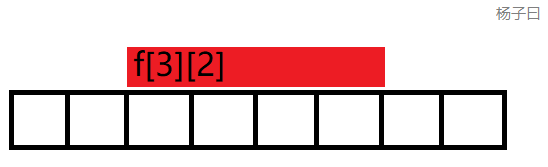
我们开一个数组 f [ i ] [ j ] f[i][j] f[i][j]表示区间 [ i , i + 2 j − 1 ] [i,i+2^j-1] [i,i+2j−1]内的最大值,也就是从 a [ i ] a[i] a[i]开始数 2 j 2^j 2j个数里面的最大值
Look at the 图,比如这就是 f [ 3 ] [ 2 ] f[3][2] f[3][2]表示的最大值区间:
好的,理解了这个数组的含义以后我们来看,怎么求出这个倍增数组?
扫一遍
初始值很简单 f [ i ] [ 0 ] = a [ i ] f[i][0]=a[i] f[i][0]=a[i]
那如何转移呢?
其实就一句话(和倍增求LCA一样):
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
很好理解吧!
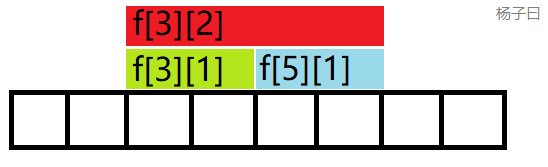
我们来举个例子,比如我们现在就是要求 f [ 3 ] [ 2 ] f[3][2] f[3][2],我们可以从 f [ 3 ] [ 1 ] f[3][1] f[3][1]和 f [ 5 ] [ 1 ] f[5][1] f[5][1]转移过来,也就是要把我们要求的区间一剖为二:
完美,我们成功把预处理的复杂度做到了O(n log n):
for (int i=1;i<=n;i++){
f[i][0]=a[i];
}
for (int j=1;j<=20;j++){//注意i和j的循环顺序
for (int i=1;i+(1<<j)-1<=n;i++){
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
好的,我们现在已经得到了f数组,那我们如何利用它去求出区间最大值呢?
区间的长度不一定是2的整数次幂呀!肿么办!!!
太简单了,比如我们要查询区间 [ 2 , 7 ] [2,7] [2,7]的最大值,我把它变成 m a x ( f [ 2 ] [ 2 ] , f [ 4 ] [ 2 ] ) max(f[2][2],f[4][2]) max(f[2][2],f[4][2]):
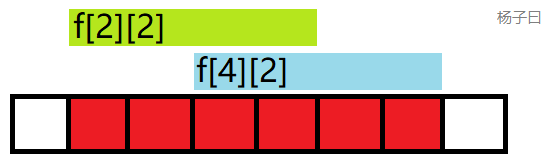
两段区间重叠在一起完全没有关系的呀!
也就是说,如果查询的区间是 [ l , r ] [l,r] [l,r],我们给出的答案就是: m a x ( f [ l ] [ l + ⌊ l o g 2 ( r − l + 1 ) ⌋ ] , f [ l − 2 ⌊ l o g 2 ( r − l + 1 ) ⌋ ] [ ⌊ l o g 2 ( r − l + 1 ) ⌋ ] ) max(f[l][l+\lfloor log_2(r-l+1) \rfloor],f[l-2^{\lfloor log_2(r-l+1) \rfloor}][\lfloor log_2(r-l+1) \rfloor]) max(f[l][l+⌊log2(r−l+1)⌋],f[l−2⌊log2(r−l+1)⌋][⌊log2(r−l+1)⌋])
仔细地研究一下这个式子,它讲的其实就是找到一个小于区间长度(r-l+1)的最大2的整数次幂,作为我们重叠的两段小区间的长度,然后取靠着左端点的这段,和靠着右端点的这段去一个max就行了!
OK,完事
c++代码(洛谷【P3865】):
#includeST表:哈哈哈,打不过我吧,没办法我就是这么强大!
线段树:你动态更新一个个我看看
ST表:……
于HG机房