c++全套流水账——染色法判断二分图,DFS的实践与应用
最近刷题比较多所以分享比较短也很少有视频了大家谅解一下。
染色法判断二分图
关于acwing
什么是二分图
二分图就是只你可以把一个图的点拉到左右两边。
这样它们就会变成两个集合。
那我们把原来图的边保留进这两个集合中。
最后如果我们可以使得这两个集合内部没有任何边,所有边都是两边互相连通的,我们称这个图为二分图。
否则不是二分图。
具体图片:
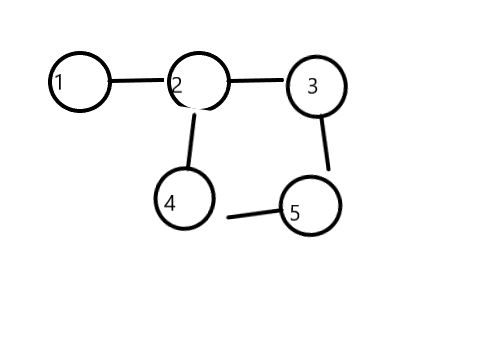
这个图是二分图吗?
是的。


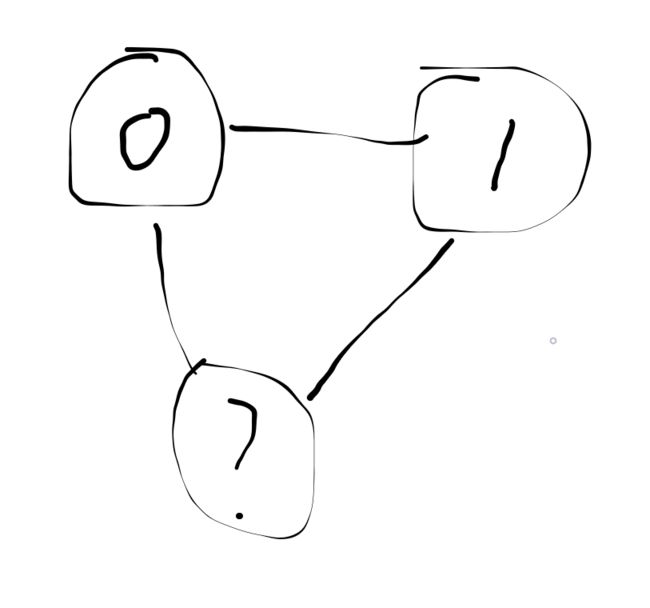
那这个呢?
不是。

好了我们一会就证明为啥第二个一定不是。
二分图的特性
其实很简单,不能有奇数环。
啥是奇数环?
就是环上的点的数量是奇数。
很简单吧。
那我们是如何证明的呢?
请看下图。
我们把一个奇数环染色。
如果我们的这个是二分图:
那我们由一条边相连的两个点的数应该是不同的。
所以我们用01标完后我们就可以把标0的点放在1号集合。
标1的点放在2号集合。
这就很弱了对吧,我们给一个奇数环标一下就知道了。
染色法判断二分图
依据上面这个原理,我们诞生了染色法。
我们可以把所有点染色撑出0,1。
那怎么染色呢?
没错就是dfs。
dfs搜索可以用来染色。
每次我们判断一下就好了。
判断一下如果我们的两个相邻的点染色相同,则这个图不是二分图。
那这个就很简单了。
我们来看一下具体模板题。
[模板]染色法判定二分图
本题题目:
给定一个n个点m条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数n和m。
接下来m行,每行包含两个整数u和v,表示点u和点v之间存在一条边。
输出格式
如果给定图是二分图,则输出“Yes”,否则输出“No”。
数据范围
1≤n,m≤1e5
输入样例:
4 4
1 3
1 4
2 3
2 4
输出样例:
Yes
首先我们看一下数据范围。
数据范围是100000,我们再+一个10。
const int N = 100010;
或者:
const int N = 1e5 + 10;
接下来是读入。
这个就很简单了。
我们只要调用add函数存一个邻接表就行了。
注意是邻接表不是邻接矩阵!!!
一:
const int N = 100010;
int n, m, h[N], e[N], ne[N], idx, color[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
二:
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i ++)
{
int a,b;
cin >> a >> b;
add(a, b);
}
memset那行很重要!如果一不小心忘写了……
就挖了……
有一次就因为这玩意找了半个小时的bug,最后自闭了/误
然后我们来看看中间这个部分。
我们的的dfs有这么几个参数:
- u,表示需要染色的点
- c,表示染的颜色
所以:
bool dfs(int u, int c)
然后我们来想一下怎么判断。
我们遍历一遍所有点然后看一下染色结果就行了。
这个也没啥好讲的。
bool f = true;
for(int i = 1; i <= n; i ++)
{
if(!color[i])
{
if(!dfs(i, 0))
{
f = false;
break;
}
}
}
接着我们来说一下dfs部分怎么写。
首先标记这个点。
color[u] = c;
接下来我们遍历一下。
for(int i = h[u]; i != -1; i = ne[i])
用j表示这个点。
int j = e[i];
接下来看一下这个点有没有染过色,如果没染过就继续往深里执行。
这不就是DFS吗?我好能水
if(!color[j])
{
if(!dfs(j, 3 - c)) return false;
}
否则我们判断一下两个点染的色是否一样。
一样就返回false。
else if(color[j] == c) return false;
这里的color就是这个被遍历到的点染的色。
c就是这个点染的色。
所以判断这俩东西是否相等就行了。
最后如果这波都挺下来了就返回true。
dfs部分完整代码:
bool dfs(int u, int c)
{
color[u] = c;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(!color[j])
{
if(!dfs(j, 3 - c)) return false;
}
else if(color[j] == c) return false;
}
return true;
}
输出我就不水了,大家看完整代码吧。
#include
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int color[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool dfs(int u, int c)
{
color[u] = c;
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(!color[j])
{
if(!dfs(j, 3 - c)) return false;
}
else if(color[j] == c) return false;
}
return true;
}
int main()
{
cin >> n >> m;
for(int i = 0; i < m; i ++)
{
int a,b;
cin >> a >> b;
add(a, b);
}
bool f = true;
for(int i = 1; i <= n; i ++)
{
if(!color[i])
{
if(!dfs(i, 0))
{
f = false;
break;
}
}
}
if(f) cout << "Yes";
else cout << "No";
return 0;
}