Fast Gradient Sign Attack（FGSM）算法小结

Fast Gradient Sign Attack（FGSM）算法小结

---

对抗攻击引发了机器学习一系列的思考，训练出来的model是否拥有强大的泛化能力？模型的准确率是否真实？
在对抗攻击中添加一些肉眼无法识别的噪声可能会对识别效果产生巨大的影响。

什么是对抗攻击

对抗攻击的核心思想就是人为地制造干扰项去迷惑模型，使模型产生错误的结果。在计算机视觉中，对抗攻击就是在原图上添加一些人为无法识别的噪声生成干扰图片，使得模型作出错误的判断。

对抗攻击分类

无目标的对抗攻击：只是让目标模型的判断出错

有目标的对抗攻击：引导目标模型做出我们想要错误判断

以对目标模型的了解程度为标准，对抗攻击又可以分成白盒攻击和黑盒攻击

白盒攻击：在已经获取机器学习模型内部的所有信息和参数上进行攻击

黑盒攻击：在神经网络结构为黑箱时，仅通过模型的输入和输出，逆推生成对抗样本。

FGSM算法原理

直观来看就是在输入的基础上沿损失函数的梯度方向加入了一定的噪声，使目标模型产生了误判。
如下图所示：原图加上超参数 ϵ 乘与 损失梯度生成新的干扰图片。

如下图所示为生成干扰图片的完整公式：x*表示对抗样本，x表示原样本，J() 表示损失函数，ϵ 表示超参数。

对于某个特定的模型而言，FGSM将损失函数近似线性化（对于神经网络而言，很多神经网络为了节省计算上的代价，都被设计成了非常线性的形式，这使得他们更容易优化，但是这样”廉价”的网络也导致了对于对抗扰动的脆弱性）。

也就是说，即是是神经网络这样的模型，也能通过线性干扰来对它进行攻击。

FGSM实例

导入所需包

import torch
from torchvision import datasets, transforms
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt

初始化超参数等全局变量

epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "../datasets/lenet_mnist_model.pth"  # 使用的预训练模型路径
use_cuda=True

定义网络结构

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()

        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()

        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)


    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))

        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)

        return F.log_softmax(x, dim=1)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../datasets', train=False, download=True, transform=transforms.Compose([
        transforms.ToTensor(),
    ])),
    batch_size=1, shuffle=True
)
device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")

model = Net().to(device)

model.load_state_dict(torch.load(pretrained_model, map_location='cpu'))
model.eval()

定义对抗图片生成函数

def fgsm_attack(image, epsilon, data_grad):
    """
    获取扰动图片
    :param image: 原始图片
    :param epsilon: 扰动量
    :param data_grad: 损失梯度
    :return:
    """
    # Collect the element-wise sign of the data gradient
    sign_data_grad = data_grad.sign()

    # Create the perturbed image by adjusting each pixel of the input image
    perturbed_image = image + epsilon*sign_data_grad

    # Adding clipping to maintain [0,1] range
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    # Return the perturbed image
    return perturbed_image

测试函数定义

def test(model, device, test_loader, epsilon):
    # Accuracy counter
    correct = 0
    adv_examples = []

    for data, target in test_loader:

        data, target = data.to(device), target.to(device)

        # Set requires_grad attribute of tensor. Important for Attack
        data.requires_grad = True

        output = model(data)
        init_pred = output.max(1, keepdim=True)[1]

        if init_pred.item() != target.item():
            continue

        # loss
        loss = F.nll_loss(output, target) # 用于多分类的负对数似然损失函数（Negative Log Likelihood) loss(x,label)=−xlabel

        model.zero_grad()

        loss.backward()

        # Collect datagrad
        data_grad = data.grad.data

        perturbed_data = fgsm_attack(data, epsilon, data_grad)
        output = model(perturbed_data)
        final_pred = output.max(1, keepdim=True)[1]

        if final_pred.item() == target.item():
            correct += 1
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(), final_pred.item(), adv_ex))
        else:
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(), final_pred.item(), adv_ex))

    # Calculate final accuracy for this epsilon
    final_acc = correct / float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))

    # Return the accuracy and an adversarial example
    return final_acc, adv_examples

开始测试

accuracies = []
examples = []
for eps in epsilons:
    acc, ex = test(model, device, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

# Plot several examples of adversarial samples at each epsilon
cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title("{} -> {}".format(orig, adv))
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

下图所示为测试结果图：

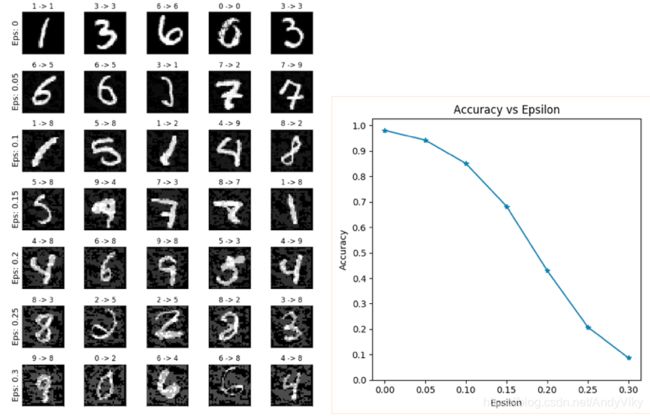
最后得出超参数 ϵ 越大(但是不超过 1 )生成的干扰图片就越有效。

完整代码:
https://github.com/AndyandViky/ML-study/blob/master/pytorch/adversarial-example.py
Reference
https://undefinedf.github.io/2018/11/02/对抗攻击之FGSM/
https://pytorch.org/tutorials/beginner/fgsm_tutorial.html