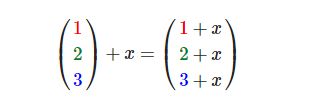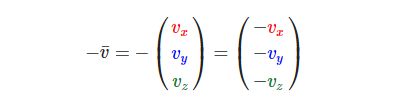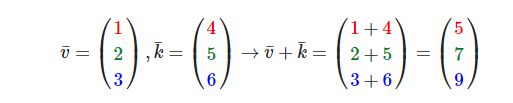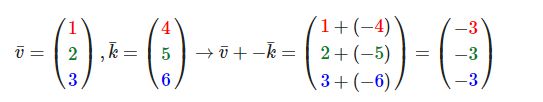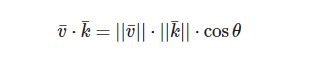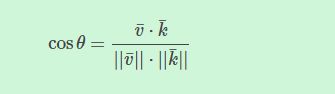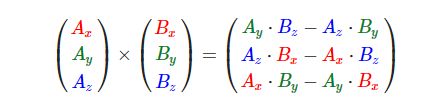3D数据基础——向量介绍与3D向量类的实现
向量
向量最基本的定义就是一个方向。或者更正式的说,向量有一个方向(Direction)和大小(Magnitude,也叫做强度或长度);向量可以在任意维度(Dimension)上,但是我们通常只使用2至4维。如果一个向量有2个维度,它表示一个平面的方向(想象一下2D的图像),当它有3个维度的时候它可以表达一个3D世界的方向。
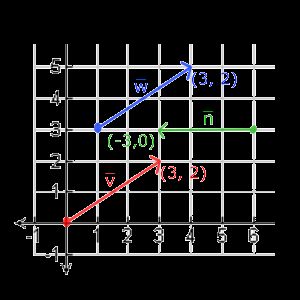
下面你会看到3个向量,每个向量在2D图像中都用一个箭头(x, y)表示。我们在2D图片中展示这些向量,因为这样子会更直观一点。你可以把这些2D向量当做z坐标为0的3D向量。由于向量表示的是方向,起始于何处并不会改变它的值。下图我们可以看到向量v¯v¯和w¯w¯是相等的,尽管他们的起始点不同:
由于向量是一个方向,所以有些时候会很难形象地将它们用位置(Position)表示出来。为了让其更为直观,我们通常设定这个方向的原点为(0, 0, 0),然后指向一个方向,对应一个点,使其变为位置向量(Position Vector)(你也可以把起点设置为其他的点,然后说:这个向量从这个点起始指向另一个点)。比如说位置向量(3, 5)在图像中的起点会是(0, 0),并会指向(3, 5)。我们可以使用向量在2D或3D空间中表示方向与位置.
1. 向量与标量的运算
标量(Scalar)只是一个数字(或者说是仅有一个分量的向量)。当把一个向量加/减/乘/除一个标量,我们可以简单的把向量的每个分量分别进行该运算。对于加法来说会像这样:
2. 负向量
对一个向量取反会将其方向逆转;在一个向量的每一个分量前加负号就可以取反了(或者向量乘以标量-1);
3. 向量的大小
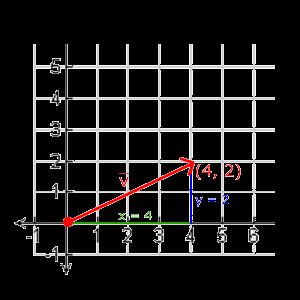
使用勾股定理(Pythagoras Theorem)来获取向量的长度(Length)/大小(Magnitude)。如果你把向量的x与y分量画出来,该向量会和x与y分量为边形成一个三角形:
4. 向量的加减
向量的加法可以被定义为是分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量:
向量v = (4, 2)和k = (1, 2)可以直观地表示为:
就像普通数字的加减一样,向量的减法等于加上第二个向量的相反向量:
两个向量的相减会得到这两个向量指向位置的差。这在我们想要获取两点的差会非常有用。
5. 标准化向量
有一个特殊类型的向量叫做单位向量(Unit Vector)。单位向量有一个特别的性质——它的长度是1。我们可以用任意向量的每个分量除以向量的长度得到它的单位向量n^n^:
我们把这种方法叫做一个向量的标准化(Normalizing)。单位向量头上有一个^样子的记号。通常单位向量会变得很有用,特别是在我们只关心方向不关心长度的时候(如果改变向量的长度,它的方向并不会改变)。
6. 向量点乘
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。可能听起来有点费解,我们来看一下公式:
可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的长度之积,得到的结果就是夹角的余弦值,即cosθ。通过上面点乘定义式可推出:
点乘的计算:
7. 向量叉乘
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。接下来的教程中这会非常有用。下面的图片展示了3D空间中叉乘的样子:
两个相交向量A和B的叉乘:
3D向量类实现
#pragma once
#include
class Vector3 {
public:
float x, y, z;
//构造函数
//默认构造函数,不执行任何操作
Vector3() {}
//复制构造函数
Vector3(const Vector3 &V)
:x(V.x)
,y(V.y)
,z(V.z){}
//带参数的构造函数,用三个值完成初始化
Vector3(float nx, float ny, float nz)
:x(nx)
,y(ny)
,z(nz){}
//重载赋值运算符,并返回引用,以实现左值
Vector3 & operator = (const Vector3& v)
{
x = v.x;
y = v.y;
z = v.z;
return *this;
}
//重载 == 操作符
bool operator == (const Vector3& v)
{
return x == v.x && y == v.y && z == v.z;
}
//重载 != 操作符
bool operator != (const Vector3 &v)
{
return x != v.x || y != v.y || z != v.z;
}
//置为0向量
void zero() { x = y = z = 0; }
//重载一元“-”操作符
Vector3 operator-() const
{
return Vector3(-x,-y,-z);
}
//重载+ 和 - 运算符
Vector3 operator+(const Vector3& v)
{
return Vector3(x + v.x, y + v.y, z + v.z);
}
Vector3 operator-(const Vector3& v)
{
return Vector3(x - v.x,y - v.y,z - v.z);
}
//与标量的乘法
Vector3 operator*(float a) const
{
return Vector3(a*x,a*y,a*z);
}
//与标量的除法
Vector3 operator/(float a)const
{
float oneOverA = 1.0f / a;//这里不对a是否为0 进行检查
return Vector3(x*oneOverA,y*oneOverA,z*oneOverA);
}
//重载自反运算符
Vector3& operator +=(const Vector3 &v)
{
x += v.x;
y += v.y;
z += v.z;
return *this;
}
Vector3& operator -=(const Vector3 &v)
{
x -= v.x;
y -= v.y;
z -= v.z;
return *this;
}
Vector3& operator *=(float a)
{
x *= a;
y *= a;
z *= a;
return *this;
}
Vector3& operator /=(float a)
{
float oneOverA = 1.0f / a;
x *= oneOverA;
y *= oneOverA;
z *= oneOverA;
return *this;
}
//向量标准化
void normalize()
{
float maqSq = x*x + y*y + z*z;
if (maqSq > 0.0f)
{
float oneOverMag = 1.0f / sqrt(maqSq);
x *= oneOverMag;
y *= oneOverMag;
z *= oneOverMag;
}
}
//向量点乘
float operator * (const Vector3& v)
{
return (x*v.x + y*v.y + z*v.z);
}
};
/********************************************************************
*
*非成员变量
*
********************************************************************/
//求向量模
inline float vectotMag(const Vector3 &v)
{
return sqrt(v.x*v.x + v.y*v.y + v.z*v.z);
}
//计算两个向量的叉乘
inline Vector3 crossProduct(const Vector3& v1, const Vector3& v2)
{
return Vector3(
v1.y*v2.z - v1.z*v2.y,
v1.z*v2.x - v1.x*v2.z,
v1.x*v2.y - v1.y*v2.x);
}
//实现标量左乘
inline Vector3 operator* (float k, const Vector3 &v)
{
return Vector3(k*v.x,k*v.y,k*v.z);
}
//计算两点之间的距离
inline float distance(const Vector3& a, const Vector3& b)
{
float dx = a.x - b.x;
float dy = a.y - b.y;
float dz = a.z - b.z;
return sqrt(dx*dx + dy*dy + dz*dz);
}
/***********************************************************************
*
*全局变量
*
************************************************************************/
//提供一个全局向量
extern const Vector3 kZeroVector; unreal4 FVector源码
//来自unreal4源码: FVector
//供参考阅读
// Copyright 1998-2015 Epic Games, Inc. All Rights Reserved.
#pragma once
/**
* A vector in 3-D space composed of components (X, Y, Z) with floating point precision.
*/
struct FVector
{
public:
/** Vector's X component. */
float X;
/** Vector's Y component. */
float Y;
/** Vector's Z component. */
float Z;
public:
/** A zero vector (0,0,0) */
static CORE_API const FVector ZeroVector;
/** World up vector (0,0,1) */
static CORE_API const FVector UpVector;
/** Unreal forward vector (1,0,0) */
static CORE_API const FVector ForwardVector;
/** Unreal right vector (0,1,0) */
static CORE_API const FVector RightVector;
public:
#if ENABLE_NAN_DIAGNOSTIC
FORCEINLINE void DiagnosticCheckNaN() const
{
checkf(!ContainsNaN(), TEXT("FVector contains NaN: %s"), *ToString());
}
#else
FORCEINLINE void DiagnosticCheckNaN() const {}
#endif
/** Default constructor (no initialization). */
FORCEINLINE FVector();
/**
* Constructor initializing all components to a single float value.
*
* @param InF Value to set all components to.
*/
explicit FORCEINLINE FVector(float InF);
/**
* Constructor using initial values for each component.
*
* @param InX X Coordinate.
* @param InY Y Coordinate.
* @param InZ Z Coordinate.
*/
FORCEINLINE FVector( float InX, float InY, float InZ );
/**
* Constructs a vector from an FVector2D and Z value.
*
* @param V Vector to copy from.
* @param InZ Z Coordinate.
*/
explicit FORCEINLINE FVector( const FVector2D V, float InZ );
/**
* Constructor using the XYZ components from a 4D vector.
*
* @param V 4D Vector to copy from.
*/
FORCEINLINE FVector( const FVector4& V );
/**
* Constructs a vector from an FLinearColor.
*
* @param InColor Color to copy from.
*/
explicit FVector(const FLinearColor& InColor);
/**
* Constructs a vector from an FIntVector.
*
* @param InVector FIntVector to copy from.
*/
explicit FVector(FIntVector InVector);
/**
* Constructs a vector from an FIntPoint.
*
* @param A Int Point used to set X and Y coordinates, Z is set to zero.
*/
explicit FVector( FIntPoint A );
/**
* Constructor which initializes all components to zero.
*
* @param EForceInit Force init enum
*/
explicit FORCEINLINE FVector(EForceInit);
#ifdef IMPLEMENT_ASSIGNMENT_OPERATOR_MANUALLY
/**
* Copy another FVector into this one
*
* @param Other The other vector.
* @return Reference to vector after copy.
*/
FORCEINLINE FVector& operator=(const FVector& Other);
#endif
/**
* Calculate cross product between this and another vector.
*
* @param V The other vector.
* @return The cross product.
*/
FORCEINLINE FVector operator^( const FVector& V ) const;
/**
* Calculate the cross product of two vectors.
*
* @param A The first vector.
* @param B The second vector.
* @return The cross product.
*/
FORCEINLINE static FVector CrossProduct( const FVector& A, const FVector& B );
/**
* Calculate the dot product between this and another vector.
*
* @param V The other vector.
* @return The dot product.
*/
FORCEINLINE float operator|( const FVector& V ) const;
/**
* Calculate the dot product of two vectors.
*
* @param A The first vector.
* @param B The second vector.
* @return The dot product.
*/
FORCEINLINE static float DotProduct( const FVector& A, const FVector& B );
/**
* Gets the result of component-wise addition of this and another vector.
*
* @param V The vector to add to this.
* @return The result of vector addition.
*/
FORCEINLINE FVector operator+( const FVector& V ) const;
/**
* Gets the result of component-wise subtraction of this by another vector.
*
* @param V The vector to subtract from this.
* @return The result of vector subtraction.
*/
FORCEINLINE FVector operator-( const FVector& V ) const;
/**
* Gets the result of subtracting from each component of the vector.
*
* @param Bias How much to subtract from each component.
* @return The result of subtraction.
*/
FORCEINLINE FVector operator-( float Bias ) const;
/**
* Gets the result of adding to each component of the vector.
*
* @param Bias How much to add to each component.
* @return The result of addition.
*/
FORCEINLINE FVector operator+( float Bias ) const;
/**
* Gets the result of scaling the vector (multiplying each component by a value).
*
* @param Scale What to multiply each component by.
* @return The result of multiplication.
*/
FORCEINLINE FVector operator*( float Scale ) const;
/**
* Gets the result of dividing each component of the vector by a value.
*
* @param Scale What to divide each component by.
* @return The result of division.
*/
FVector operator/( float Scale ) const;
/**
* Gets the result of component-wise multiplication of this vector by another.
*
* @param V The vector to multiply with.
* @return The result of multiplication.
*/
FORCEINLINE FVector operator*( const FVector& V ) const;
/**
* Gets the result of component-wise division of this vector by another.
*
* @param V The vector to divide by.
* @return The result of division.
*/
FORCEINLINE FVector operator/( const FVector& V ) const;
// Binary comparison operators.
/**
* Check against another vector for equality.
*
* @param V The vector to check against.
* @return true if the vectors are equal, false otherwise.
*/
bool operator==( const FVector& V ) const;
/**
* Check against another vector for inequality.
*
* @param V The vector to check against.
* @return true if the vectors are not equal, false otherwise.
*/
bool operator!=( const FVector& V ) const;
/**
* Check against another vector for equality, within specified error limits.
*
* @param V The vector to check against.
* @param Tolerance Error tolerance.
* @return true if the vectors are equal within tolerance limits, false otherwise.
*/
bool Equals(const FVector& V, float Tolerance=KINDA_SMALL_NUMBER) const;
/**
* Checks whether all components of this vector are the same, within a tolerance.
*
* @param Tolerance Error tolerance.
* @return true if the vectors are equal within tolerance limits, false otherwise.
*/
bool AllComponentsEqual(float Tolerance=KINDA_SMALL_NUMBER) const;
/**
* Get a negated copy of the vector.
*
* @return A negated copy of the vector.
*/
FORCEINLINE FVector operator-() const;
/**
* Adds another vector to this.
* Uses component-wise addition.
*
* @param V Vector to add to this.
* @return Copy of the vector after addition.
*/
FORCEINLINE FVector operator+=( const FVector& V );
/**
* Subtracts another vector from this.
* Uses component-wise subtraction.
*
* @param V Vector to subtract from this.
* @return Copy of the vector after subtraction.
*/
FORCEINLINE FVector operator-=( const FVector& V );
/**
* Scales the vector.
*
* @param Scale Amount to scale this vector by.
* @return Copy of the vector after scaling.
*/
FORCEINLINE FVector operator*=( float Scale );
/**
* Divides the vector by a number.
*
* @param V What to divide this vector by.
* @return Copy of the vector after division.
*/
FVector operator/=( float V );
/**
* Multiplies the vector with another vector, using component-wise multiplication.
*
* @param V What to multiply this vector with.
* @return Copy of the vector after multiplication.
*/
FVector operator*=( const FVector& V );
/**
* Divides the vector by another vector, using component-wise division.
*
* @param V What to divide vector by.
* @return Copy of the vector after division.
*/
FVector operator/=( const FVector& V );
/**
* Gets specific component of the vector.
*
* @param Index the index of vector component
* @return reference to component.
*/
float& operator[]( int32 Index );
/**
* Gets specific component of the vector.
*
* @param Index the index of vector component
* @return Copy of the component.
*/
float operator[]( int32 Index )const;
/**
* Gets a specific component of the vector.
*
* @param Index The index of the component required.
*
* @return Reference to the specified component.
*/
float& Component(int32 Index);
/**
* Gets a specific component of the vector.
*
* @param Index The index of the component required.
* @return Copy of the specified component.
*/
float Component(int32 Index) const;
// Simple functions.
/**
* Set the values of the vector directly.
*
* @param InX New X coordinate.
* @param InY New Y coordinate.
* @param InZ New Z coordinate.
*/
void Set( float InX, float InY, float InZ );
/**
* Get the maximum value of the vector's components.
*
* @return The maximum value of the vector's components.
*/
float GetMax() const;
/**
* Get the maximum absolute value of the vector's components.
*
* @return The maximum absolute value of the vector's components.
*/
float GetAbsMax() const;
/**
* Get the minimum value of the vector's components.
*
* @return The minimum value of the vector's components.
*/
float GetMin() const;
/**
* Get the minimum absolute value of the vector's components.
*
* @return The minimum absolute value of the vector's components.
*/
float GetAbsMin() const;
/** Gets the component-wise min of two vectors. */
FVector ComponentMin(const FVector& Other) const;
/** Gets the component-wise max of two vectors. */
FVector ComponentMax(const FVector& Other) const;
/**
* Get a copy of this vector with absolute value of each component.
*
* @return A copy of this vector with absolute value of each component.
*/
FVector GetAbs() const;
/**
* Get the length (magnitude) of this vector.
*
* @return The length of this vector.
*/
float Size() const;
/**
* Get the squared length of this vector.
*
* @return The squared length of this vector.
*/
float SizeSquared() const;
/**
* Get the length of the 2D components of this vector.
*
* @return The 2D length of this vector.
*/
float Size2D() const ;
/**
* Get the squared length of the 2D components of this vector.
*
* @return The squared 2D length of this vector.
*/
float SizeSquared2D() const ;
/**
* Checks whether vector is near to zero within a specified tolerance.
*
* @param Tolerance Error tolerance.
* @return true if the vector is near to zero, false otherwise.
*/
bool IsNearlyZero(float Tolerance=KINDA_SMALL_NUMBER) const;
/**
* Checks whether all components of the vector are exactly zero.
*
* @return true if the vector is exactly zero, false otherwise.
*/
bool IsZero() const;
/**
* Normalize this vector in-place if it is large enough, set it to (0,0,0) otherwise.
*
* @param Tolerance Minimum squared length of vector for normalization.
* @return true if the vector was normalized correctly, false otherwise.
*/
bool Normalize(float Tolerance=SMALL_NUMBER);
/**
* Checks whether vector is normalized.
*
* @return true if Normalized, false otherwise.
*/
bool IsNormalized() const;
/**
* Util to convert this vector into a unit direction vector and its original length.
*
* @param OutDir Reference passed in to store unit direction vector.
* @param OutLength Reference passed in to store length of the vector.
*/
void ToDirectionAndLength(FVector &OutDir, float &OutLength) const;
/**
* Get a copy of the vector as sign only.
* Each component is set to +1 or -1, with the sign of zero treated as +1.
*
* @param A copy of the vector with each component set to +1 or -1
*/
FORCEINLINE FVector GetSignVector() const;
/**
* Projects 2D components of vector based on Z.
*
* @return Projected version of vector based on Z.
*/
FVector Projection() const;
/**
* Calculates normalized version of vector without checking for zero length.
*
* @return Normalized version of vector.
* @see GetSafeNormal()
*/
FORCEINLINE FVector GetUnsafeNormal() const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetUnsafeNormal instead.")
FORCEINLINE FVector UnsafeNormal() const;
/**
* Gets a copy of this vector snapped to a grid.
*
* @param GridSz Grid dimension.
* @return A copy of this vector snapped to a grid.
* @see FMath::GridSnap()
*/
FVector GridSnap( const float& GridSz ) const;
/**
* Get a copy of this vector, clamped inside of a cube.
*
* @param Radius Half size of the cube.
* @return A copy of this vector, bound by cube.
*/
FVector BoundToCube( float Radius ) const;
/** Create a copy of this vector, with its magnitude clamped between Min and Max. */
FVector GetClampedToSize(float Min, float Max) const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetClampedToSize instead.")
FVector ClampSize(float Min, float Max) const;
/** Create a copy of this vector, with the 2D magnitude clamped between Min and Max. Z is unchanged. */
FVector GetClampedToSize2D(float Min, float Max) const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetClampedToSize2D instead.")
FVector ClampSize2D(float Min, float Max) const;
/** Create a copy of this vector, with its maximum magnitude clamped to MaxSize. */
FVector GetClampedToMaxSize(float MaxSize) const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetClampedToMaxSize instead.")
FVector ClampMaxSize(float MaxSize) const;
/** Create a copy of this vector, with the maximum 2D magnitude clamped to MaxSize. Z is unchanged. */
FVector GetClampedToMaxSize2D(float MaxSize) const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetClampedToMaxSize2D instead.")
FVector ClampMaxSize2D(float MaxSize) const;
/**
* Add a vector to this and clamp the result in a cube.
*
* @param V Vector to add.
* @param Radius Half size of the cube.
*/
void AddBounded( const FVector& V, float Radius=MAX_int16 );
/**
* Gets the reciprocal of this vector, avoiding division by zero.
* Zero components are set to BIG_NUMBER.
*
* @return Reciprocal of this vector.
*/
FVector Reciprocal() const;
/**
* Check whether X, Y and Z are nearly equal.
*
* @param Tolerance Specified Tolerance.
* @return true if X == Y == Z within the specified tolerance.
*/
bool IsUniform(float Tolerance=KINDA_SMALL_NUMBER) const;
/**
* Mirror a vector about a normal vector.
*
* @param MirrorNormal Normal vector to mirror about.
* @return Mirrored vector.
*/
FVector MirrorByVector( const FVector& MirrorNormal ) const;
/**
* Mirrors a vector about a plane.
*
* @param Plane Plane to mirror about.
* @return Mirrored vector.
*/
FVector MirrorByPlane( const FPlane& Plane ) const;
/**
* Rotates around Axis (assumes Axis.Size() == 1).
*
* @param Angle Angle to rotate (in degrees).
* @param Axis Axis to rotate around.
* @return Rotated Vector.
*/
FVector RotateAngleAxis( const float AngleDeg, const FVector& Axis ) const;
/**
* Gets a normalized copy of the vector, checking it is safe to do so based on the length.
* Returns zero vector if vector length is too small to safely normalize.
*
* @param Tolerance Minimum squared vector length.
* @return A normalized copy if safe, (0,0,0) otherwise.
*/
FVector GetSafeNormal(float Tolerance=SMALL_NUMBER) const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetSafeNormal instead.")
FVector SafeNormal(float Tolerance = SMALL_NUMBER) const;
/**
* Gets a normalized copy of the 2D components of the vector, checking it is safe to do so. Z is set to zero.
* Returns zero vector if vector length is too small to normalize.
*
* @param Tolerance Minimum squared vector length.
* @return Normalized copy if safe, otherwise returns zero vector.
*/
FVector GetSafeNormal2D(float Tolerance=SMALL_NUMBER) const;
DEPRECATED(4.7, "Deprecated due to unclear name, use GetSafeNormal2D instead.")
FVector SafeNormal2D(float Tolerance = SMALL_NUMBER) const;
/**
* Returns the cosine of the angle between this vector and another projected onto the XY plane (no Z).
*
* @param B the other vector to find the 2D cosine of the angle with.
* @return The cosine.
*/
FORCEINLINE float CosineAngle2D(FVector B) const;
/**
* Gets a copy of this vector projected onto the input vector.
*
* @param A Vector to project onto, does not assume it is normalized.
* @return Projected vector.
*/
FORCEINLINE FVector ProjectOnTo( const FVector& A ) const ;
/**
* Gets a copy of this vector projected onto the input vector, which is assumed to be unit length.
*
* @param Normal Vector to project onto (assumed to be unit length).
* @return Projected vector.
*/
FORCEINLINE FVector ProjectOnToNormal(const FVector& Normal ) const;
/**
* Return the FRotator corresponding to the direction that the vector
* is pointing in. Sets Yaw and Pitch to the proper numbers, and sets
* roll to zero because the roll can't be determined from a vector.
*
* @return The FRotator from the vector's direction.
*/
CORE_API FRotator Rotation() const;
/**
* Find good arbitrary axis vectors to represent U and V axes of a plane,
* using this vector as the normal of the plane.
*
* @param Axis1 Reference to first axis.
* @param Axis2 Reference to second axis.
*/
CORE_API void FindBestAxisVectors( FVector& Axis1, FVector& Axis2 ) const;
/** When this vector contains Euler angles (degrees), ensure that angles are between +/-180 */
CORE_API void UnwindEuler();
/**
* Utility to check if there are any NaNs in this vector.
*
* @return true if there are any NaNs in this vector, false otherwise.
*/
bool ContainsNaN() const;
/**
* Check if the vector is of unit length, with specified tolerance.
*
* @param LengthSquaredTolerance Tolerance against squared length.
* @return true if the vector is a unit vector within the specified tolerance.
*/
FORCEINLINE bool IsUnit(float LengthSquaredTolerance = KINDA_SMALL_NUMBER ) const;
/**
* Get a textual representation of this vector.
*
* @return A string describing the vector.
*/
FString ToString() const;
/**
* Get a locale aware textual representation of this vector.
*
* @return A string describing the vector.
*/
FText ToText() const;
/** Get a short textural representation of this vector, for compact readable logging. */
FString ToCompactString() const;
/** Get a short locale aware textural representation of this vector, for compact readable logging. */
FText ToCompactText() const;
/**
* Initialize this Vector based on an FString. The String is expected to contain X=, Y=, Z=.
* The FVector will be bogus when InitFromString returns false.
*
* @param InSourceString FString containing the vector values.
* @return true if the X,Y,Z values were read successfully; false otherwise.
*/
bool InitFromString( const FString& InSourceString );
/**
* Converts a Cartesian unit vector into spherical coordinates on the unit sphere.
* @return Output Theta will be in the range [0, PI], and output Phi will be in the range [-PI, PI].
*/
FVector2D UnitCartesianToSpherical() const;
/**
* Convert a direction vector into a 'heading' angle.
*
* @return 'Heading' angle between +/-PI. 0 is pointing down +X.
*/
float HeadingAngle() const;
/**
* Create an orthonormal basis from a basis with at least two orthogonal vectors.
* It may change the directions of the X and Y axes to make the basis orthogonal,
* but it won't change the direction of the Z axis.
* All axes will be normalized.
*
* @param XAxis The input basis' XAxis, and upon return the orthonormal basis' XAxis.
* @param YAxis The input basis' YAxis, and upon return the orthonormal basis' YAxis.
* @param ZAxis The input basis' ZAxis, and upon return the orthonormal basis' ZAxis.
*/
static CORE_API void CreateOrthonormalBasis(FVector& XAxis,FVector& YAxis,FVector& ZAxis);
/**
* Compare two points and see if they're the same, using a threshold.
*
* @param P First vector.
* @param Q Second vector.
* @return Whether points are the same within a threshold. Uses fast distance approximation (linear per-component distance).
*/
static bool PointsAreSame( const FVector &P, const FVector &Q );
/**
* Compare two points and see if they're within specified distance.
*
* @param Point1 First vector.
* @param Point2 Second vector.
* @param Dist Specified distance.
* @return Whether two points are within the specified distance. Uses fast distance approximation (linear per-component distance).
*/
static bool PointsAreNear( const FVector &Point1, const FVector &Point2, float Dist );
/**
* Calculate the signed distance (in the direction of the normal) between a point and a plane.
*
* @param Point The Point we are checking.
* @param PlaneBase The Base Point in the plane.
* @param PlaneNormal The Normal of the plane (assumed to be unit length).
* @return Signed distance between point and plane.
*/
static float PointPlaneDist( const FVector &Point, const FVector &PlaneBase, const FVector &PlaneNormal );
/**
* Calculate the projection of a point on the given plane.
*
* @param Point The point to project onto the plane
* @param Plane The plane
* @return Projection of Point onto Plane
*/
static FVector PointPlaneProject(const FVector& Point, const FPlane& Plane);
/**
* Calculate the projection of a point on the plane defined by counter-clockwise (CCW) points A,B,C.
*
* @param Point The point to project onto the plane
* @param A 1st of three points in CCW order defining the plane
* @param B 2nd of three points in CCW order defining the plane
* @param C 3rd of three points in CCW order defining the plane
* @return Projection of Point onto plane ABC
*/
static FVector PointPlaneProject(const FVector& Point, const FVector& A, const FVector& B, const FVector& C);
/**
* Calculate the projection of a point on the plane defined by PlaneBase and PlaneNormal.
*
* @param Point The point to project onto the plane
* @param PlaneBase Point on the plane
* @param PlaneNorm Normal of the plane (assumed to be unit length).
* @return Projection of Point onto plane
*/
static FVector PointPlaneProject(const FVector& Point, const FVector& PlaneBase, const FVector& PlaneNormal);
/**
* Calculate the projection of a vector on the plane defined by PlaneNormal.
*
* @param V The vector to project onto the plane.
* @param PlaneNormal Normal of the plane (assumed to be unit length).
* @return Projection of V onto plane.
*/
static FVector VectorPlaneProject(const FVector& V, const FVector& PlaneNormal);
/**
* Euclidean distance between two points.
*
* @param V1 The first point.
* @param V2 The second point.
* @return The distance between two points.
*/
static FORCEINLINE float Dist( const FVector &V1, const FVector &V2 );
/**
* Squared distance between two points.
*
* @param V1 The first point.
* @param V2 The second point.
* @return The squared distance between two points.
*/
static FORCEINLINE float DistSquared( const FVector &V1, const FVector &V2 );
/**
* Compute pushout of a box from a plane.
*
* @param Normal The plane normal.
* @param Size The size of the box.
* @return Pushout required.
*/
static FORCEINLINE float BoxPushOut( const FVector& Normal, const FVector& Size );
/**
* See if two normal vectors are nearly parallel, meaning the angle between them is close to 0 degrees.
*
* @param Normal1 First normalized vector.
* @param Normal1 Second normalized vector.
* @param ParallelCosineThreshold Normals are parallel if absolute value of dot product (cosine of angle between them) is greater than or equal to this. For example: cos(1.0 degrees).
* @return true if vectors are nearly parallel, false otherwise.
*/
static bool Parallel(const FVector& Normal1, const FVector& Normal2, float ParallelCosineThreshold = THRESH_NORMALS_ARE_PARALLEL);
/**
* See if two normal vectors are coincident (nearly parallel and point in the same direction).
*
* @param Normal1 First normalized vector.
* @param Normal2 Second normalized vector.
* @param ParallelCosineThreshold Normals are coincident if dot product (cosine of angle between them) is greater than or equal to this. For example: cos(1.0 degrees).
* @return true if vectors are coincident (nearly parallel and point in the same direction), false otherwise.
*/
static bool Coincident(const FVector& Normal1, const FVector& Normal2, float ParallelCosineThreshold = THRESH_NORMALS_ARE_PARALLEL);
/**
* See if two normal vectors are nearly orthogonal (perpendicular), meaning the angle between them is close to 90 degrees.
*
* @param Normal1 First normalized vector.
* @param Normal2 Second normalized vector.
* @param OrthogonalCosineThreshold Normals are orthogonal if absolute value of dot product (cosine of angle between them) is less than or equal to this. For example: cos(89.0 degrees).
* @return true if vectors are orthogonal (perpendicular), false otherwise.
*/
static bool Orthogonal(const FVector& Normal1, const FVector& Normal2, float OrthogonalCosineThreshold = THRESH_NORMALS_ARE_ORTHOGONAL);
/**
* See if two planes are coplanar. They are coplanar if the normals are nearly parallel and the planes include the same set of points.
*
* @param Base1 The base point in the first plane.
* @param Normal1 The normal of the first plane.
* @param Base2 The base point in the second plane.
* @param Normal2 The normal of the second plane.
* @param ParallelCosineThreshold Normals are parallel if absolute value of dot product is greater than or equal to this.
* @return true if the planes are coplanar, false otherwise.
*/
static bool Coplanar(const FVector& Base1, const FVector& Normal1, const FVector& Base2, const FVector& Normal2, float ParallelCosineThreshold = THRESH_NORMALS_ARE_PARALLEL);
/**
* Triple product of three vectors: X dot (Y cross Z).
*
* @param X The first vector.
* @param Y The second vector.
* @param Z The third vector.
* @return The triple product: X dot (Y cross Z).
*/
static float Triple( const FVector& X, const FVector& Y, const FVector& Z );
/**
* Generates a list of sample points on a Bezier curve defined by 2 points.
*
* @param ControlPoints Array of 4 FVectors (vert1, controlpoint1, controlpoint2, vert2).
* @param NumPoints Number of samples.
* @param OutPoints Receives the output samples.
* @return The path length.
*/
static CORE_API float EvaluateBezier(const FVector* ControlPoints, int32 NumPoints, TArray& OutPoints);
/**
* Converts a vector containing radian values to a vector containing degree values.
*
* @param RadVector Vector containing radian values
* @return Vector containing degree values
*/
static FVector RadiansToDegrees(const FVector& RadVector);
/**
* Converts a vector containing degree values to a vector containing radian values.
*
* @param DegVector Vector containing degree values
* @return Vector containing radian values
*/
static FVector DegreesToRadians(const FVector& DegVector);
/**
* Given a current set of cluster centers, a set of points, iterate N times to move clusters to be central.
*
* @param Clusters Reference to array of Clusters.
* @param Points Set of points.
* @param NumIterations Number of iterations.
* @param NumConnectionsToBeValid Sometimes you will have long strings that come off the mass of points
* which happen to have been chosen as Cluster starting points. You want to be able to disregard those.
*/
static CORE_API void GenerateClusterCenters(TArray& Clusters, const TArray& Points, int32 NumIterations, int32 NumConnectionsToBeValid);
/**
* Serializer.
*
* @param Ar Serialization Archive.
* @param V Vector to serialize.
* @return Reference to Archive after serialization.
*/
friend FArchive& operator<<( FArchive& Ar, FVector& V )
{
// @warning BulkSerialize: FVector is serialized as memory dump
// See TArray::BulkSerialize for detailed description of implied limitations.
return Ar << V.X << V.Y << V.Z;
}
/**
* Network serialization function.
* FVectors NetSerialize without quantization (ie exact values are serialized).
*
* @see FVector_NetQuantize, FVector_NetQuantize10, FVector_NetQuantize100, FVector_NetQuantizeNormal
*/
CORE_API bool NetSerialize(FArchive& Ar, class UPackageMap* Map, bool& bOutSuccess);
};
/* FVector inline functions
*****************************************************************************/
/**
* Multiplies a vector by a scaling factor.
*
* @param Scale Scaling factor.
* @param V Vector to scale.
* @return Result of multiplication.
*/
FORCEINLINE FVector operator*( float Scale, const FVector& V )
{
return V.operator*( Scale );
}
/**
* Creates a hash value from a FVector.
*
* @param Vector the vector to create a hash value for
* @return The hash value from the components
*/
FORCEINLINE uint32 GetTypeHash(const FVector& Vector)
{
// Note: this assumes there's no padding in FVector that could contain uncompared data.
return FCrc::MemCrc_DEPRECATED(&Vector,sizeof(Vector));
}
/**
* Creates a hash value from a FVector2D.
*
* @param Vector the vector to create a hash value for
* @return The hash value from the components
*/
FORCEINLINE uint32 GetTypeHash(const FVector2D& Vector)
{
// Note: this assumes there's no padding in FVector2D that could contain uncompared data.
return FCrc::MemCrc_DEPRECATED(&Vector,sizeof(Vector));
}
#if PLATFORM_LITTLE_ENDIAN
#define INTEL_ORDER_VECTOR(x) (x)
#else
static FORCEINLINE FVector INTEL_ORDER_VECTOR(FVector v)
{
return FVector(INTEL_ORDERF(v.X), INTEL_ORDERF(v.Y), INTEL_ORDERF(v.Z));
}
#endif
/**
* Util to calculate distance from a point to a bounding box
*
* @param Mins 3D Point defining the lower values of the axis of the bound box
* @param Max 3D Point defining the lower values of the axis of the bound box
* @param Point 3D position of interest
* @return the distance from the Point to the bounding box.
*/
FORCEINLINE float ComputeSquaredDistanceFromBoxToPoint( const FVector& Mins, const FVector& Maxs, const FVector& Point )
{
// Accumulates the distance as we iterate axis
float DistSquared = 0.f;
// Check each axis for min/max and add the distance accordingly
// NOTE: Loop manually unrolled for > 2x speed up
if (Point.X < Mins.X)
{
DistSquared += FMath::Square(Point.X - Mins.X);
}
else if (Point.X > Maxs.X)
{
DistSquared += FMath::Square(Point.X - Maxs.X);
}
if (Point.Y < Mins.Y)
{
DistSquared += FMath::Square(Point.Y - Mins.Y);
}
else if (Point.Y > Maxs.Y)
{
DistSquared += FMath::Square(Point.Y - Maxs.Y);
}
if (Point.Z < Mins.Z)
{
DistSquared += FMath::Square(Point.Z - Mins.Z);
}
else if (Point.Z > Maxs.Z)
{
DistSquared += FMath::Square(Point.Z - Maxs.Z);
}
return DistSquared;
}
FORCEINLINE FVector::FVector( const FVector2D V, float InZ )
: X(V.X), Y(V.Y), Z(InZ)
{
DiagnosticCheckNaN();
}
inline FVector FVector::RotateAngleAxis( const float AngleDeg, const FVector& Axis ) const
{
float S, C;
FMath::SinCos(&S, &C, FMath::DegreesToRadians(AngleDeg));
const float XX = Axis.X * Axis.X;
const float YY = Axis.Y * Axis.Y;
const float ZZ = Axis.Z * Axis.Z;
const float XY = Axis.X * Axis.Y;
const float YZ = Axis.Y * Axis.Z;
const float ZX = Axis.Z * Axis.X;
const float XS = Axis.X * S;
const float YS = Axis.Y * S;
const float ZS = Axis.Z * S;
const float OMC = 1.f - C;
return FVector(
(OMC * XX + C ) * X + (OMC * XY - ZS) * Y + (OMC * ZX + YS) * Z,
(OMC * XY + ZS) * X + (OMC * YY + C ) * Y + (OMC * YZ - XS) * Z,
(OMC * ZX - YS) * X + (OMC * YZ + XS) * Y + (OMC * ZZ + C ) * Z
);
}
inline bool FVector::PointsAreSame( const FVector &P, const FVector &Q )
{
float Temp;
Temp=P.X-Q.X;
if( (Temp > -THRESH_POINTS_ARE_SAME) && (Temp < THRESH_POINTS_ARE_SAME) )
{
Temp=P.Y-Q.Y;
if( (Temp > -THRESH_POINTS_ARE_SAME) && (Temp < THRESH_POINTS_ARE_SAME) )
{
Temp=P.Z-Q.Z;
if( (Temp > -THRESH_POINTS_ARE_SAME) && (Temp < THRESH_POINTS_ARE_SAME) )
{
return true;
}
}
}
return false;
}
inline bool FVector::PointsAreNear( const FVector &Point1, const FVector &Point2, float Dist )
{
float Temp;
Temp=(Point1.X - Point2.X); if (FMath::Abs(Temp)>=Dist) return false;
Temp=(Point1.Y - Point2.Y); if (FMath::Abs(Temp)>=Dist) return false;
Temp=(Point1.Z - Point2.Z); if (FMath::Abs(Temp)>=Dist) return false;
return true;
}
inline float FVector::PointPlaneDist
(
const FVector &Point,
const FVector &PlaneBase,
const FVector &PlaneNormal
)
{
return (Point - PlaneBase) | PlaneNormal;
}
inline FVector FVector::PointPlaneProject(const FVector& Point, const FVector& PlaneBase, const FVector& PlaneNorm)
{
//Find the distance of X from the plane
//Add the distance back along the normal from the point
return Point - FVector::PointPlaneDist(Point,PlaneBase,PlaneNorm) * PlaneNorm;
}
inline FVector FVector::VectorPlaneProject(const FVector& V, const FVector& PlaneNormal)
{
return V - V.ProjectOnToNormal(PlaneNormal);
}
inline bool FVector::Parallel(const FVector& Normal1, const FVector& Normal2, float ParallelCosineThreshold)
{
const float NormalDot = Normal1 | Normal2;
return FMath::Abs(NormalDot) >= ParallelCosineThreshold;
}
inline bool FVector::Coincident(const FVector& Normal1, const FVector& Normal2, float ParallelCosineThreshold)
{
const float NormalDot = Normal1 | Normal2;
return NormalDot >= ParallelCosineThreshold;
}
inline bool FVector::Orthogonal(const FVector& Normal1, const FVector& Normal2, float OrthogonalCosineThreshold)
{
const float NormalDot = Normal1 | Normal2;
return FMath::Abs(NormalDot) <= OrthogonalCosineThreshold;
}
inline bool FVector::Coplanar(const FVector &Base1, const FVector &Normal1, const FVector &Base2, const FVector &Normal2, float ParallelCosineThreshold)
{
if (!FVector::Parallel(Normal1,Normal2,ParallelCosineThreshold)) return false;
else if (FVector::PointPlaneDist (Base2,Base1,Normal1) > THRESH_POINT_ON_PLANE) return false;
else return true;
}
inline float FVector::Triple( const FVector& X, const FVector& Y, const FVector& Z )
{
return
( (X.X * (Y.Y * Z.Z - Y.Z * Z.Y))
+ (X.Y * (Y.Z * Z.X - Y.X * Z.Z))
+ (X.Z * (Y.X * Z.Y - Y.Y * Z.X)) );
}
inline FVector FVector::RadiansToDegrees(const FVector& RadVector)
{
return RadVector * (180.f / PI);
}
inline FVector FVector::DegreesToRadians(const FVector& DegVector)
{
return DegVector * (PI / 180.f);
}
FORCEINLINE FVector::FVector()
{}
FORCEINLINE FVector::FVector(float InF)
: X(InF), Y(InF), Z(InF)
{
DiagnosticCheckNaN();
}
FORCEINLINE FVector::FVector( float InX, float InY, float InZ )
: X(InX), Y(InY), Z(InZ)
{
DiagnosticCheckNaN();
}
FORCEINLINE FVector::FVector(const FLinearColor& InColor)
: X(InColor.R), Y(InColor.G), Z(InColor.B)
{
DiagnosticCheckNaN();
}
FORCEINLINE FVector::FVector(FIntVector InVector)
: X(InVector.X), Y(InVector.Y), Z(InVector.Z)
{
DiagnosticCheckNaN();
}
FORCEINLINE FVector::FVector( FIntPoint A )
: X(A.X), Y(A.Y), Z(0.f)
{
DiagnosticCheckNaN();
}
FORCEINLINE FVector::FVector(EForceInit)
: X(0.0f), Y(0.0f), Z(0.0f)
{
DiagnosticCheckNaN();
}
#ifdef IMPLEMENT_ASSIGNMENT_OPERATOR_MANUALLY
FORCEINLINE FVector& FVector::operator=(const FVector& Other)
{
this->X = Other.X;
this->Y = Other.Y;
this->Z = Other.Z;
DiagnosticCheckNaN();
return *this;
}
#endif
FORCEINLINE FVector FVector::operator^( const FVector& V ) const
{
return FVector
(
Y * V.Z - Z * V.Y,
Z * V.X - X * V.Z,
X * V.Y - Y * V.X
);
}
FORCEINLINE FVector FVector::CrossProduct( const FVector& A, const FVector& B )
{
return A ^ B;
}
FORCEINLINE float FVector::operator|( const FVector& V ) const
{
return X*V.X + Y*V.Y + Z*V.Z;
}
FORCEINLINE float FVector::DotProduct( const FVector& A, const FVector& B )
{
return A | B;
}
FORCEINLINE FVector FVector::operator+( const FVector& V ) const
{
return FVector( X + V.X, Y + V.Y, Z + V.Z );
}
FORCEINLINE FVector FVector::operator-( const FVector& V ) const
{
return FVector( X - V.X, Y - V.Y, Z - V.Z );
}
FORCEINLINE FVector FVector::operator-( float Bias ) const
{
return FVector( X - Bias, Y - Bias, Z - Bias );
}
FORCEINLINE FVector FVector::operator+( float Bias ) const
{
return FVector( X + Bias, Y + Bias, Z + Bias );
}
FORCEINLINE FVector FVector::operator*( float Scale ) const
{
return FVector( X * Scale, Y * Scale, Z * Scale );
}
FORCEINLINE FVector FVector::operator/( float Scale ) const
{
const float RScale = 1.f/Scale;
return FVector( X * RScale, Y * RScale, Z * RScale );
}
FORCEINLINE FVector FVector::operator*( const FVector& V ) const
{
return FVector( X * V.X, Y * V.Y, Z * V.Z );
}
FORCEINLINE FVector FVector::operator/( const FVector& V ) const
{
return FVector( X / V.X, Y / V.Y, Z / V.Z );
}
FORCEINLINE bool FVector::operator==( const FVector& V ) const
{
return X==V.X && Y==V.Y && Z==V.Z;
}
FORCEINLINE bool FVector::operator!=( const FVector& V ) const
{
return X!=V.X || Y!=V.Y || Z!=V.Z;
}
FORCEINLINE bool FVector::Equals(const FVector& V, float Tolerance) const
{
return FMath::Abs(X-V.X) <= Tolerance && FMath::Abs(Y-V.Y) <= Tolerance && FMath::Abs(Z-V.Z) <= Tolerance;
}
FORCEINLINE bool FVector::AllComponentsEqual(float Tolerance) const
{
return FMath::Abs( X - Y ) < Tolerance && FMath::Abs( X - Z ) < Tolerance && FMath::Abs( Y - Z ) < Tolerance;
}
FORCEINLINE FVector FVector::operator-() const
{
return FVector( -X, -Y, -Z );
}
FORCEINLINE FVector FVector::operator+=( const FVector& V )
{
X += V.X; Y += V.Y; Z += V.Z;
DiagnosticCheckNaN();
return *this;
}
FORCEINLINE FVector FVector::operator-=( const FVector& V )
{
X -= V.X; Y -= V.Y; Z -= V.Z;
DiagnosticCheckNaN();
return *this;
}
FORCEINLINE FVector FVector::operator*=( float Scale )
{
X *= Scale; Y *= Scale; Z *= Scale;
DiagnosticCheckNaN();
return *this;
}
FORCEINLINE FVector FVector::operator/=( float V )
{
const float RV = 1.f/V;
X *= RV; Y *= RV; Z *= RV;
DiagnosticCheckNaN();
return *this;
}
FORCEINLINE FVector FVector::operator*=( const FVector& V )
{
X *= V.X; Y *= V.Y; Z *= V.Z;
DiagnosticCheckNaN();
return *this;
}
FORCEINLINE FVector FVector::operator/=( const FVector& V )
{
X /= V.X; Y /= V.Y; Z /= V.Z;
DiagnosticCheckNaN();
return *this;
}
FORCEINLINE float& FVector::operator[]( int32 Index )
{
check(Index >= 0 && Index < 3);
if( Index == 0 )
{
return X;
}
else if( Index == 1)
{
return Y;
}
else
{
return Z;
}
}
FORCEINLINE float FVector::operator[]( int32 Index )const
{
check(Index >= 0 && Index < 3);
if( Index == 0 )
{
return X;
}
else if( Index == 1)
{
return Y;
}
else
{
return Z;
}
}
FORCEINLINE void FVector::Set( float InX, float InY, float InZ )
{
X = InX;
Y = InY;
Z = InZ;
DiagnosticCheckNaN();
}
FORCEINLINE float FVector::GetMax() const
{
return FMath::Max(FMath::Max(X,Y),Z);
}
FORCEINLINE float FVector::GetAbsMax() const
{
return FMath::Max(FMath::Max(FMath::Abs(X),FMath::Abs(Y)),FMath::Abs(Z));
}
FORCEINLINE float FVector::GetMin() const
{
return FMath::Min(FMath::Min(X,Y),Z);
}
FORCEINLINE float FVector::GetAbsMin() const
{
return FMath::Min(FMath::Min(FMath::Abs(X),FMath::Abs(Y)),FMath::Abs(Z));
}
FORCEINLINE FVector FVector::ComponentMin(const FVector& Other) const
{
return FVector(FMath::Min(X, Other.X), FMath::Min(Y, Other.Y), FMath::Min(Z, Other.Z));
}
FORCEINLINE FVector FVector::ComponentMax(const FVector& Other) const
{
return FVector(FMath::Max(X, Other.X), FMath::Max(Y, Other.Y), FMath::Max(Z, Other.Z));
}
FORCEINLINE FVector FVector::GetAbs() const
{
return FVector(FMath::Abs(X), FMath::Abs(Y), FMath::Abs(Z));
}
FORCEINLINE float FVector::Size() const
{
return FMath::Sqrt( X*X + Y*Y + Z*Z );
}
FORCEINLINE float FVector::SizeSquared() const
{
return X*X + Y*Y + Z*Z;
}
FORCEINLINE float FVector::Size2D() const
{
return FMath::Sqrt( X*X + Y*Y );
}
FORCEINLINE float FVector::SizeSquared2D() const
{
return X*X + Y*Y;
}
FORCEINLINE bool FVector::IsNearlyZero(float Tolerance) const
{
return
FMath::Abs(X) Tolerance )
{
const float Scale = FMath::InvSqrt(SquareSum);
X *= Scale; Y *= Scale; Z *= Scale;
return true;
}
return false;
}
FORCEINLINE bool FVector::IsNormalized() const
{
return (FMath::Abs(1.f - SizeSquared()) < THRESH_VECTOR_NORMALIZED);
}
FORCEINLINE void FVector::ToDirectionAndLength(FVector &OutDir, float &OutLength) const
{
OutLength = Size();
if (OutLength > SMALL_NUMBER)
{
float OneOverLength = 1.0f/OutLength;
OutDir = FVector(X*OneOverLength, Y*OneOverLength,
Z*OneOverLength);
}
else
{
OutDir = FVector::ZeroVector;
}
}
FORCEINLINE FVector FVector::GetSignVector() const
{
return FVector
(
FMath::FloatSelect(X, 1.f, -1.f),
FMath::FloatSelect(Y, 1.f, -1.f),
FMath::FloatSelect(Z, 1.f, -1.f)
);
}
FORCEINLINE FVector FVector::Projection() const
{
const float RZ = 1.f/Z;
return FVector( X*RZ, Y*RZ, 1 );
}
FORCEINLINE FVector FVector::GetUnsafeNormal() const
{
const float Scale = FMath::InvSqrt(X*X+Y*Y+Z*Z);
return FVector( X*Scale, Y*Scale, Z*Scale );
}
FORCEINLINE FVector FVector::UnsafeNormal() const
{
return GetUnsafeNormal();
}
FORCEINLINE FVector FVector::GridSnap( const float& GridSz ) const
{
return FVector( FMath::GridSnap(X, GridSz),FMath::GridSnap(Y, GridSz),FMath::GridSnap(Z, GridSz) );
}
FORCEINLINE FVector FVector::BoundToCube( float Radius ) const
{
return FVector
(
FMath::Clamp(X,-Radius,Radius),
FMath::Clamp(Y,-Radius,Radius),
FMath::Clamp(Z,-Radius,Radius)
);
}
FORCEINLINE FVector FVector::GetClampedToSize(float Min, float Max) const
{
float VecSize = Size();
const FVector VecDir = (VecSize > SMALL_NUMBER) ? (*this/VecSize) : FVector::ZeroVector;
VecSize = FMath::Clamp(VecSize, Min, Max);
return VecSize * VecDir;
}
FORCEINLINE FVector FVector::ClampSize(float Min, float Max) const
{
return GetClampedToSize(Min, Max);
}
FORCEINLINE FVector FVector::GetClampedToSize2D(float Min, float Max) const
{
float VecSize2D = Size2D();
const FVector VecDir = (VecSize2D > SMALL_NUMBER) ? (*this/VecSize2D) : FVector::ZeroVector;
VecSize2D = FMath::Clamp(VecSize2D, Min, Max);
return FVector(VecSize2D * VecDir.X, VecSize2D * VecDir.Y, Z);
}
FORCEINLINE FVector FVector::ClampSize2D(float Min, float Max) const
{
return GetClampedToSize2D(Min, Max);
}
FORCEINLINE FVector FVector::GetClampedToMaxSize(float MaxSize) const
{
if (MaxSize < KINDA_SMALL_NUMBER)
{
return FVector::ZeroVector;
}
const float VSq = SizeSquared();
if (VSq > FMath::Square(MaxSize))
{
const float Scale = MaxSize * FMath::InvSqrt(VSq);
return FVector(X*Scale, Y*Scale, Z*Scale);
}
else
{
return *this;
}
}
FORCEINLINE FVector FVector::ClampMaxSize(float MaxSize) const
{
return GetClampedToMaxSize(MaxSize);
}
FORCEINLINE FVector FVector::GetClampedToMaxSize2D(float MaxSize) const
{
if (MaxSize < KINDA_SMALL_NUMBER)
{
return FVector(0.f, 0.f, Z);
}
const float VSq2D = SizeSquared2D();
if (VSq2D > FMath::Square(MaxSize))
{
const float Scale = MaxSize * FMath::InvSqrt(VSq2D);
return FVector(X*Scale, Y*Scale, Z);
}
else
{
return *this;
}
}
FORCEINLINE FVector FVector::ClampMaxSize2D(float MaxSize) const
{
return GetClampedToMaxSize2D(MaxSize);
}
FORCEINLINE void FVector::AddBounded( const FVector& V, float Radius )
{
*this = (*this + V).BoundToCube(Radius);
}
FORCEINLINE float& FVector::Component( int32 Index )
{
return (&X)[Index];
}
FORCEINLINE float FVector::Component( int32 Index ) const
{
return (&X)[Index];
}
FORCEINLINE FVector FVector::Reciprocal() const
{
FVector RecVector;
if (X!=0.f)
{
RecVector.X = 1.f/X;
}
else
{
RecVector.X = BIG_NUMBER;
}
if (Y!=0.f)
{
RecVector.Y = 1.f/Y;
}
else
{
RecVector.Y = BIG_NUMBER;
}
if (Z!=0.f)
{
RecVector.Z = 1.f/Z;
}
else
{
RecVector.Z = BIG_NUMBER;
}
return RecVector;
}
FORCEINLINE bool FVector::IsUniform(float Tolerance) const
{
return (FMath::Abs(X-Y) < Tolerance) && (FMath::Abs(Y-Z) < Tolerance);
}
FORCEINLINE FVector FVector::MirrorByVector( const FVector& MirrorNormal ) const
{
return *this - MirrorNormal * (2.f * (*this | MirrorNormal));
}
FORCEINLINE FVector FVector::GetSafeNormal(float Tolerance) const
{
const float SquareSum = X*X + Y*Y + Z*Z;
// Not sure if it's safe to add tolerance in there. Might introduce too many errors
if( SquareSum == 1.f )
{
return *this;
}
else if( SquareSum < Tolerance )
{
return FVector::ZeroVector;
}
const float Scale = FMath::InvSqrt(SquareSum);
return FVector(X*Scale, Y*Scale, Z*Scale);
}
FORCEINLINE FVector FVector::SafeNormal(float Tolerance) const
{
return GetSafeNormal(Tolerance);
}
FORCEINLINE FVector FVector::GetSafeNormal2D(float Tolerance) const
{
const float SquareSum = X*X + Y*Y;
// Not sure if it's safe to add tolerance in there. Might introduce too many errors
if( SquareSum == 1.f )
{
if( Z == 0.f )
{
return *this;
}
else
{
return FVector(X, Y, 0.f);
}
}
else if( SquareSum < Tolerance )
{
return FVector::ZeroVector;
}
const float Scale = FMath::InvSqrt(SquareSum);
return FVector(X*Scale, Y*Scale, 0.f);
}
FORCEINLINE FVector FVector::SafeNormal2D(float Tolerance) const
{
return GetSafeNormal2D(Tolerance);
}
FORCEINLINE float FVector::CosineAngle2D(FVector B) const
{
FVector A(*this);
A.Z = 0.0f;
B.Z = 0.0f;
A.Normalize();
B.Normalize();
return A | B;
}
FORCEINLINE FVector FVector::ProjectOnTo( const FVector& A ) const
{
return (A * ((*this | A) / (A | A)));
}
FORCEINLINE FVector FVector::ProjectOnToNormal(const FVector& Normal) const
{
return (Normal * (*this | Normal));
}
FORCEINLINE bool FVector::ContainsNaN() const
{
return (FMath::IsNaN(X) || !FMath::IsFinite(X) ||
FMath::IsNaN(Y) || !FMath::IsFinite(Y) ||
FMath::IsNaN(Z) || !FMath::IsFinite(Z));
}
FORCEINLINE bool FVector::IsUnit(float LengthSquaredTolerance ) const
{
return FMath::Abs(1.0f - SizeSquared()) < LengthSquaredTolerance;
}
FORCEINLINE FString FVector::ToString() const
{
return FString::Printf(TEXT("X=%3.3f Y=%3.3f Z=%3.3f"), X, Y, Z);
}
FORCEINLINE FText FVector::ToText() const
{
FFormatNamedArguments Args;
Args.Add(TEXT("X"), X);
Args.Add(TEXT("Y"), Y);
Args.Add(TEXT("Z"), Z);
return FText::Format(NSLOCTEXT("Core", "Vector3", "X={X} Y={Y} Z={Z}"), Args);
}
FORCEINLINE FText FVector::ToCompactText() const
{
if (IsNearlyZero())
{
return NSLOCTEXT("Core", "Vector3_CompactZeroVector", "V(0)");
}
const bool XIsNotZero = !FMath::IsNearlyZero(X);
const bool YIsNotZero = !FMath::IsNearlyZero(Y);
const bool ZIsNotZero = !FMath::IsNearlyZero(Z);
FNumberFormattingOptions FormatRules;
FormatRules.MinimumFractionalDigits = 2;
FormatRules.MinimumIntegralDigits = 0;
FFormatNamedArguments Args;
Args.Add(TEXT("X"), FText::AsNumber(X, &FormatRules));
Args.Add(TEXT("Y"), FText::AsNumber(Y, &FormatRules));
Args.Add(TEXT("Z"), FText::AsNumber(Z, &FormatRules));
if (XIsNotZero && YIsNotZero && ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactXYZ", "V(X={X}, Y={Y}, Z={Z})"), Args);
}
else if (!XIsNotZero && YIsNotZero && ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactYZ", "V(Y={Y}, Z={Z})"), Args);
}
else if (XIsNotZero && !YIsNotZero && ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactXZ", "V(X={X}, Z={Z})"), Args);
}
else if (XIsNotZero && YIsNotZero && !ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactXY", "V(X={X}, Y={Y})"), Args);
}
else if (!XIsNotZero && !YIsNotZero && ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactZ", "V(Z={Z})"), Args);
}
else if (XIsNotZero && !YIsNotZero && !ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactX", "V(X={X})"), Args);
}
else if (!XIsNotZero && YIsNotZero && !ZIsNotZero)
{
return FText::Format(NSLOCTEXT("Core", "Vector3_CompactY", "V(Y={Y})"), Args);
}
return NSLOCTEXT("Core", "Vector3_CompactZeroVector", "V(0)");
}
FORCEINLINE FString FVector::ToCompactString() const
{
if( IsNearlyZero() )
{
return FString::Printf(TEXT("V(0)"));
}
FString ReturnString(TEXT("V("));
bool bIsEmptyString = true;
if( !FMath::IsNearlyZero(X) )
{
ReturnString += FString::Printf(TEXT("X=%.2f"), X);
bIsEmptyString = false;
}
if( !FMath::IsNearlyZero(Y) )
{
if( !bIsEmptyString )
{
ReturnString += FString(TEXT(", "));
}
ReturnString += FString::Printf(TEXT("Y=%.2f"), Y);
bIsEmptyString = false;
}
if( !FMath::IsNearlyZero(Z) )
{
if( !bIsEmptyString )
{
ReturnString += FString(TEXT(", "));
}
ReturnString += FString::Printf(TEXT("Z=%.2f"), Z);
bIsEmptyString = false;
}
ReturnString += FString(TEXT(")"));
return ReturnString;
}
FORCEINLINE bool FVector::InitFromString( const FString& InSourceString )
{
X = Y = Z = 0;
// The initialization is only successful if the X, Y, and Z values can all be parsed from the string
const bool bSuccessful = FParse::Value( *InSourceString, TEXT("X=") , X ) && FParse::Value( *InSourceString, TEXT("Y="), Y ) && FParse::Value( *InSourceString, TEXT("Z="), Z );
return bSuccessful;
}
FORCEINLINE FVector2D FVector::UnitCartesianToSpherical() const
{
checkSlow(IsUnit());
const float Theta = FMath::Acos(Z / Size());
const float Phi = FMath::Atan2(Y, X);
return FVector2D(Theta, Phi);
}
FORCEINLINE float FVector::HeadingAngle() const
{
// Project Dir into Z plane.
FVector PlaneDir = *this;
PlaneDir.Z = 0.f;
PlaneDir = PlaneDir.GetSafeNormal();
float Angle = FMath::Acos(PlaneDir.X);
if(PlaneDir.Y < 0.0f)
{
Angle *= -1.0f;
}
return Angle;
}
FORCEINLINE float FVector::Dist( const FVector &V1, const FVector &V2 )
{
return FMath::Sqrt( FMath::Square(V2.X-V1.X) + FMath::Square(V2.Y-V1.Y) + FMath::Square(V2.Z-V1.Z) );
}
FORCEINLINE float FVector::DistSquared( const FVector &V1, const FVector &V2 )
{
return FMath::Square(V2.X-V1.X) + FMath::Square(V2.Y-V1.Y) + FMath::Square(V2.Z-V1.Z);
}
FORCEINLINE float FVector::BoxPushOut( const FVector& Normal, const FVector& Size )
{
return FMath::Abs(Normal.X*Size.X) + FMath::Abs(Normal.Y*Size.Y) + FMath::Abs(Normal.Z*Size.Z);
}
/** Component-wise clamp for FVector */
FORCEINLINE FVector ClampVector( const FVector& V, const FVector& Min, const FVector& Max )
{
return FVector(
FMath::Clamp(V.X,Min.X,Max.X),
FMath::Clamp(V.Y,Min.Y,Max.Y),
FMath::Clamp(V.Z,Min.Z,Max.Z)
);
}
template <> struct TIsPODType { enum { Value = true }; };
以上参考:
- 3D数学基础:图形与游戏开发
- https://learnopengl.com/
- unreal4 源码