二分查找

今天我们讲一种针对有序数据集合的查找算法：二分查找（ Binary Search ）算法，也叫折半查找算法。二分查找的思想非常简单，很多非计算机专业的同学很容易
就能理解，但是看似越简单的东西往往越难掌握好，想要灵活应用就更加困难。
老规矩，我们还是来看一道思考题。

假设我们有1000万个整数数据，每个数据占8个字节，
如何设计数据结构和算法，快速判断某个整数是否出现在这1000万数据中？

一.无处不在的二分思想

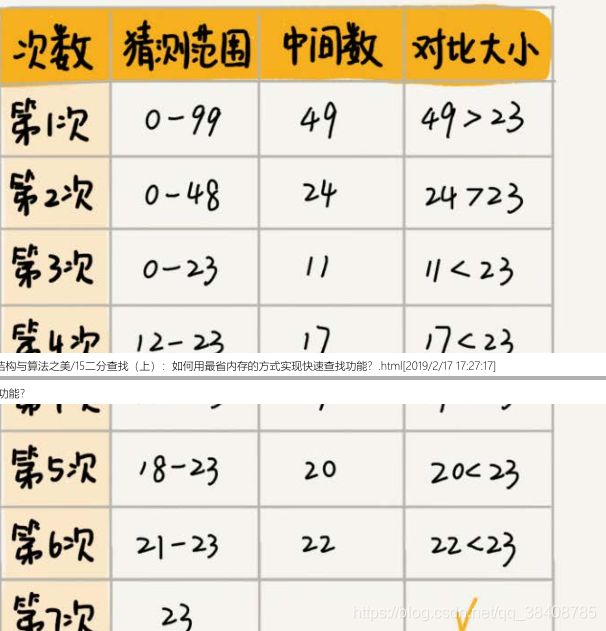
二分查找是一种非常简单易懂的快速查找算法，生活中到处可见。比如说，我们现在来做一个猜字游戏。我随机写一个 0 到 99 之间的数字，然后你来猜我写的是什
么。猜的过程中，你每猜一次，我就会告诉你猜的大了还是小了，直到猜中为止。你来想想，如何快速猜中我写的数字呢？
假设我写的数字是 23 ，你可以按照下面的步骤来试一试。（如果猜测范围的数字有偶数个，中间数有两个，就选择较小的那个。）

7 次就猜出来了，是不是很快？这个例子用的就是二分思想，按照这个思想，即便我让你猜的是 0 到 999 的数字，最多也只要 10 次就能猜中。不信的话，你可以试一
试

二.O(logn) 惊人的查找速度

二分查找是一种非常高效的查找算法，高效到什么程度呢？我们来分析一下它的时间复杂度。
我们假设数据大小是 n ，每次查找后数据都会缩小为原来的一半，也就是会除以 2 。最坏情况下，直到查找区间被缩小为空，才停止。

可以看出来，这是一个等比数列。其中n/2 k =1时，k的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较，所以，经过了k次区间缩小操作，时
间复杂度就是O(k)。通过n/2 k =1，我们可以求得k=log 2 n，所以时间复杂度就是O(logn)。

三.二分查找的递归与非递归实现

java代码

	public int bsearch(int[] a, int n, int value) {
	int low = 0;
	int high = n - 1;
	while (low <= high) {
	int mid = (low + high) / 2;
	if (a[mid] == value) {
	return mid;
	} else if (a[mid] < value) {
	low = mid + 1;
	} else {
	high = mid - 1;
	}
	}
	return -1;
}

递归实现

	public int bsearch(int[] a, int n, int val) {
	return bsearchInternally(a, 0, n - 1, val);
	}
	private int bsearchInternally(int[] a, int low, int high, int value) {
	if (low > high) return -1;
	int mid = low + ((high - low) >> 1);
	if (a[mid] == value) {
	return mid;
	} else if (a[mid] < value) {
	return bsearchInternally(a, mid+1, high, value);
	} else {
	return bsearchInternally(a, low, mid-1, value);
	}
	}

四.二分查找应用场景的局限性

1.首先，二分查找依赖的是顺序表结构，简单点说就是数组。

那二分查找能否依赖其他数据结构呢？比如链表。答案是不可以的，主要原因是二分查找算法需要按照下标随机访问元素。我们在数组和链表那两节讲过，数组
按照下标随机访问数据的时间复杂度是 O(1) ，而链表随机访问的时间复杂度是 O(n) 。所以，如果数据使用链表存储，二分查找的时间复杂就会变得很高。
二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的，则无法应用二分查找。

2.其次，二分查找针对的是有序数据。

二分查找对这一点的要求比较苛刻，数据必须是有序的。如果数据没有序，我们需要先排序。前面章节里我们讲到，排序的时间复杂度最低是 O(nlogn) 。所以，如
果我们针对的是一组静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较
低。
但是，如果我们的数据集合有频繁的插入和删除操作，要想用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排
序。针对这种动态数据集合，无论哪种方法，维护有序的成本都是很高的。
所以，二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适用。那针对动态数据集合，如何在
其中快速查找某个数据呢？答：用二叉树

3.再次，数据量太小不适合二分查找。

如果要处理的数据量很小，完全没有必要用二分查找，顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素，不管用二分查找还是顺序遍历，查
找速度都差不多。只有数据量比较大的时候，二分查找的优势才会比较明显。
不过，这里有一个例外。如果数据之间的比较操作非常耗时，不管数据量大小，我都推荐使用二分查找。比如，数组中存储的都是长度超过 300 的字符串，如此长
的两个字符串之间比对大小，就会非常耗时。我们需要尽可能地减少比较次数，而比较次数的减少会大大提高性能，这个时候二分查找就比顺序遍历更有优势。

4.最后，数据量太大也不适合二分查找。

二分查找的底层需要依赖数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。比如，我们有 1GB 大小的数据，如
1GB 如果希望用数组来存储，那就需要 的连续内存空间。
注意这里的 “ 连续 ” 二字，也就是说，即便有 2GB 的内存空间剩余，但是如果这剩余的 2GB 内存空间都是零散的，没有连续的 1GB 大小的内存空间，那照样无法申请
一个 1GB 大小的数组。而我们的二分查找是作用在数组这种数据结构之上的，所以太大的数据用数组存储就比较吃力了，也就不能用二分查找了。

五.内容小结

今天我们学习了一种针对有序数据的高效查找算法，二分查找，它的时间复杂度是 O(logn) 。
二分查找的核心思想理解起来非常简单，有点类似分治思想。即每次都通过跟区间中的中间元素对比，将待查找的区间缩小为一半，直到找到要查找的元素，或
者区间被缩小为 0 。但是二分查找的代码实现比较容易写错。你需要着重掌握它的三个容易出错的地方：循环退出条件、 mid 的取值， low 和 high 的更新。

二分查找虽然性能比较优秀，但应用场景也比较有限。底层必须依赖数组，并且还要求数据是有序的。对于较小规模的数据查找，我们直接使用顺序遍历就可以
了，二分查找的优势并不明显。二分查找更适合处理静态数据，也就是没有频繁的数据插入、删除操作。