VigenereCipher
Title: 《VigenereCipher》
Author: Hugu
Started Date: Sept. 13th. 2019
Finished Date: Oct. 27th. 2019
维吉尼亚密码
介绍:
维吉尼亚密码(又译 维热纳尔密码)是使用一系列凯撒密码组成密码字母表的加密算法,属于多表密码的一种简单形式。
维吉尼亚密码曾多次被发明。该方法最早记录在吉奥万·巴蒂斯塔·贝拉索( Giovan Battista Bellaso)于1553年所著的书《吉奥万·巴蒂斯塔·贝拉索先生的密码》中。然而,后来在19世纪时被误传为是法国外交官布莱斯·德·维吉尼亚所创造,因此现在被称为“维吉尼亚密码”。
维吉尼亚密码以其简单易用而著称,同时初学者通常难以破解,因而又被称为“不可破译的密码”。这也让很多人使用维吉尼亚密码来加密的目的就是为了将其破解。
历史:
多表密码最早在1467年左右由莱昂·巴蒂斯塔·阿尔伯蒂提出,他使用了一个金属密码盘来切换密码表,只是这个系统只能做些有限的转换。后来1508年时,约翰尼斯·特里特米乌斯《隐写术》(Steganographia)中发明的表格法(tabula recta)成为了维吉尼亚密码的关键部分。然而当时此方法只能对密码表做一些简单的、可预测的切换。这一加密技术也称为特里特米乌斯密码。
这一方法真正出现是在吉奥万·巴蒂斯塔·贝拉索于1553年所著的书《吉奥万·巴蒂斯塔·贝拉索先生的算术》中。他以特里特米乌斯的表格法为基础,同时引入了密钥的概念。
布莱斯·德·维吉尼亚于1586年亨利三世时期发明了更为简单却又更有效的自动密钥密码(autokey cipher)。之后,19世纪时贝拉索的方法被误认为是由维吉尼亚首先发明的。大卫·卡恩在《破译者(The Codebreakers)》中对此表示遗憾,他写道“历史忽略了这一重要贡献,将其归功于维吉尼亚,虽然他对此并不知道”。
由于破译的难度很高,维吉尼亚密码也因此获得了很高的声望。知名作家、数学家查尔斯·路特维奇·道奇森(笔名路易斯·卡罗)在其1868年所编、收于一儿童杂志的《字母表密码(The Alphabet Cipher)》中称其是不可破译的。1917年,《科学美国人》将维吉尼亚密码称为“无法被转化的”。然而,维吉尼亚密码却配不上这样的称号。查尔斯·巴贝奇完成了破译的工作,但他没有将此发表。之后,弗里德里希·卡西斯基(Friedrich Kasiski)于19世纪完全破解并发表了他的方法。甚至在此之前,一些资深密码分析家在16世纪就能偶尔将其破解。
维吉尼亚密码足够地易于使用使其能够作为战地密码。例如,美国南北战争期间南军就使用黄铜密码盘生成维吉尼亚密码。北军则经常能够破译南军的密码。战争自始至终,南军主要使用三个密钥,分别为“Manchester Bluff(曼彻斯特的虚张声势)”、“Complete Victory(完全的胜利)”以及战争后期的“Come Retribution(报应来临)”。
吉尔伯特·维尔南(Gilbert Vernam)曾试图对已被破译的密码进行修补(于1918年创造了维尔南-维尼吉亚密码),然而这终究无济于事。不过维尔南的发明最终促成了一次性密码本的诞生,这是一种理论上不可破译的密码。
原理解析
维吉尼亚密码可以说是凯撒密码的升级版,在凯撒密码中,字母表中的每一字母会做一定的偏移,而维吉尼亚密码可以看作是由一些偏移量不同的凯撒密码组成。
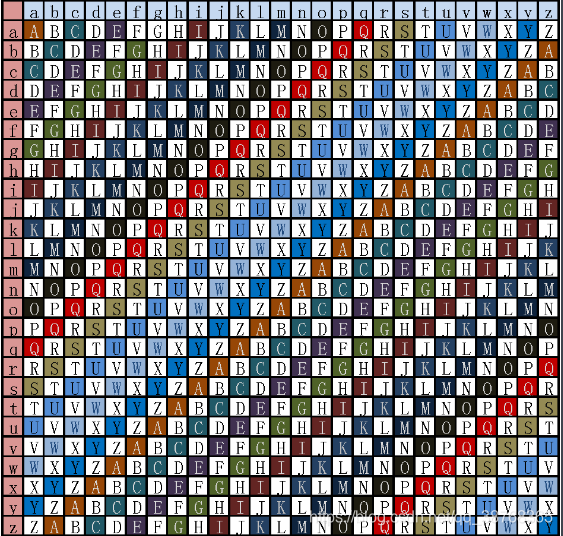
为了生成密码,需要使用表格法。这一表格(如图1所示)包括了26行字母表,每一行都由前一行向左偏移一位得到。具体使用哪一行字母表进行编译是基于密钥进行的,在过程中会不断地变换。
举个栗子:
使用的维吉尼亚密码表如下图所示:
加密:
-
假设明文为:
ATTACKATDAWN
-
LEMON为选定关键词,则密钥为:
LEMONLEMONLE
-
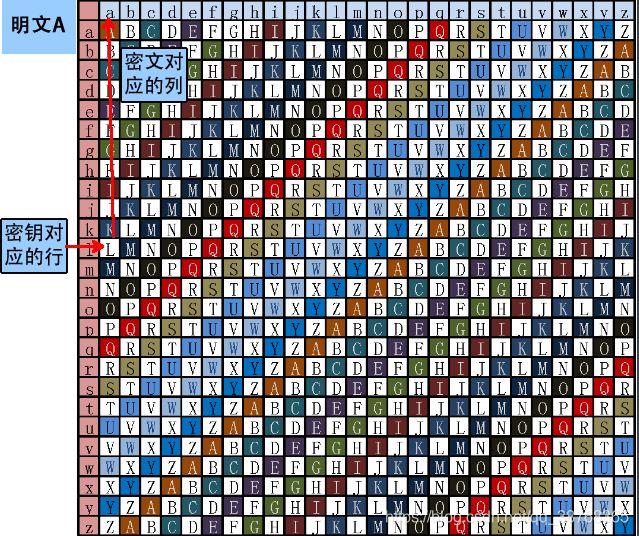
将密钥作为行标识,明文作为列标识,对明文中的字母依次替换为行列相交处的字母,则得到密文:
LXFOPVEFRNHR
明文字符串首字母的加密过程如下图所示:
解密:
-
假设密文为:
LXFOPVEFRNHR
-
LEMON为选定关键词,则密钥为:
LEMONLEMONLE
-
将密钥作为行标识,在该行内查找与其密文一样的字母,该字母对应的列值即为明文,则得到明文:
ATTACKATDAWN
密文字符串首字母的解密过程如下图所示:
数学语言描述:
- 首先将字母用数字代替,即:A=0,B=1,C=2,…,Z=25。
- 明文空间记为:M
- 密文空间记为:C
- 密钥空间记为:Km
- 将偏移量记为:kn
- 加密操作记为:E(m)
- 解密操作记为:D©
则有:
加密变换:
E ( m 1 , m 2 , . . . , m n ) = ( m 1 + k 1 m o d 26 , m 2 + k 2 m o d 26 , . . , m n + k n m o d 26 ) , ( m i ∈ M , k i ∈ K , n ∈ N ) E(m_1,m_2,...,m_n) = (m_1+k_1 \ mod \ 26,m_2+k_2 \ mod \ 26,..,m_n+k_n \ mod \ 26),(m_i∈M,k_i∈K,n∈N) E(m1,m2,...,mn)=(m1+k1 mod 26,m2+k2 mod 26,..,mn+kn mod 26),(mi∈M,ki∈K,n∈N)
解密变换:
E ( m 1 , m 2 , . . . , m n ) = ( m 1 − k 1 m o d 26 , m 2 − k 2 m o d 26 , . . , m n − k n m o d 26 ) , ( m i ∈ M , k i ∈ K , n ∈ N ) E(m_1,m_2,...,m_n) = (m_1-k_1 \ mod \ 26,m_2-k_2 \ mod \ 26,..,m_n-k_n \ mod \ 26),(m_i∈M,k_i∈K,n∈N) E(m1,m2,...,mn)=(m1−k1 mod 26,m2−k2 mod 26,..,mn−kn mod 26),(mi∈M,ki∈K,n∈N)
程序设计
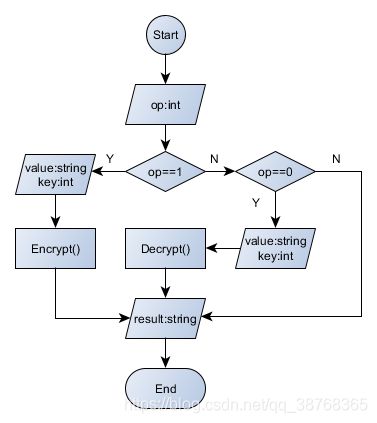
程序流程图:
- 第一次输入一个int型数据op,若
op==1则执行加密操作,若op==0则执行解密操作,否则结束程序。 - 第二次输入一个字符串,进行加密或解密操作。
- 操作结果后显示加密或解密的结果。
编程实现
Vigenere类:
using System;
using System.Text;
namespace Cryptology_Vigenere
{
class Vigenere
{
#region 定义全局变量
private char[,] codeMatrix;
#endregion
#region 构造函数
public Vigenere()
{
// 初始化对象时也初始化密码矩阵
Vigenere_InitCodeMatrix();
// 展示密码表
DisplayCipherTable();
}
#endregion
#region 初始化Vigenere密码矩阵
private void Vigenere_InitCodeMatrix()
{
codeMatrix = new char[26, 26];//矩阵
char temp;
for(int i = 0;i < 26;i++)
{
temp = 'A';
temp = (char)(temp + i);
for(int j = 0;j < 26;j++)
{
if((char)(temp + j) > 'Z')
{
codeMatrix[i, j] = (char)((temp + j) - 26);
}
else
{
codeMatrix[i, j] = (char)(temp + j);
}
}
}
}
#endregion
#region 展示维吉尼亚密码表
private void DisplayCipherTable()
{
Console.Write(" ");
for(int i = 0;i < 26;i++)
{
Console.Write((char)('a' + i) + " ");
}
Console.WriteLine();
for (int i = 0; i < 26; i++)
{
for (int j = 0; j < 26; j++)
{
if(j == 0)
{
Console.Write((char)('a' + i) + " ");
}
Console.Write(codeMatrix[i, j] + " ");
}
Console.WriteLine();
}
}
#endregion
#region Vigenere加密
/// 密文
internal string Encrypt(string plaintext, string key)
{
int x, y,k=0;//k:密钥计数器
string str = plaintext.ToUpper();
int min_mod = str.Length > key.Length ? key.Length : str.Length;
StringBuilder strBuilder = new StringBuilder();
for(int i = 0;i < str.Length;i++)
{
if(str[i] >= 'A' && str[i] <= 'Z')
{
x = str[i] - 'A';
y = key[k++ % min_mod] - 'A';
strBuilder.Append(codeMatrix[x, y]);
}
else
{
strBuilder.Append(str[i]);
}
}
return strBuilder.ToString();
}
#endregion
#region Vigenere解密
/// 明文
internal string Decrypt(string ciphertext, string key)
{
int x, y,temp,k=0;//k:密钥计数器
string str = ciphertext.ToUpper();
int min_mod = str.Length > key.Length ? key.Length : str.Length;
StringBuilder strBuilder = new StringBuilder();
for(int i = 0;i < str.Length;i++)
{
if(str[i] >= 'A' && str[i] <= 'Z')
{
y = key[k++ % min_mod] - 'A';
temp = str[i] - 'A';
if (temp < y)//是否发生回环
{
x = temp + 26 - y;
}
else
{
x = str[i] - 'A' - y;
}
strBuilder.Append((char)(x + 'A'));
}
else
{
strBuilder.Append(str[i]);
}
}
return strBuilder.ToString();
}
#endregion
}
}
注:
- 先构造一张密码表,并显示加(解)密时使用的表
- 加密时查表,解密时也查表
Program测试类:
using System;
namespace Cryptology_Vigenere
{
class Program
{
static void Main(string[] args)
{
Console.Title = "Vigenere";
int op;
string plaintext, key, ciphytext,str;
Vigenere vig = new Vigenere();
Console.Write("请输入您想要进行的操作:(1:加密,0:解密) ->");
str = Console.ReadLine();
if(int.TryParse(str,out op))
{
if (op == 1)
{
Console.Write("请输入明文:");
plaintext = Console.ReadLine();
Console.Write("请输入密钥:");
key = Console.ReadLine();
ciphytext = vig.Encrypt(plaintext, key);
Console.WriteLine(ciphytext);
}
else if (op == 0)
{
Console.Write("请输入密文");
ciphytext = Console.ReadLine();
Console.Write("请输入密钥:");
key = Console.ReadLine();
plaintext = vig.Decrypt(ciphytext, key);
Console.WriteLine(plaintext);
}
else
{
Console.WriteLine("输入错误程序停止!!!");
}
}
else
{
Console.WriteLine("输入错误程序停止!!!");
}
Console.ReadKey();
}
}
}
结果显示
加密结果:
解密结果:
密码分析1
维吉尼亚密码分解后实则就是多个凯撒密码,只要知道密钥的长度,我们就可以将其分解。
如密文为:ABCDEFGHIJKLMN
如果我们知道密钥长度为3,就可将其分解为三组:
组1:A D G J N
组2:B E H K
组3:C F I M
分解后每组就是一个凯撒密码,即组内的位移量是一致的,对每一组即可用频度分析法来解密。
所以破解维吉尼亚密码的关键就是确定密钥的长度。
确定密钥长度
确定密钥长度主要有两种方法,Kasiski 测试法相对简单很多,但Friedman 测试法的效果明显优于Kasiski 测试法。
Kasiski 测试法:
在英文中,一些常见的单词如the有几率被密钥的相同部分加密,即原文中的the可能在密文中呈现为相同的三个字母。在这种情况下,相同片段的间距就是密文长度的倍数。所以我们可以通过在密文中找到相同的片段,计算出这些相同片段之间的间距,而密钥长度理论上就是这些间距的公约数。然后我们需要知道重合指数(IC, index of coincidence)的概念。
重合指数表示两个随机选出的字母是相同的的概率,即随机选出两个A的概率+随机选出两个B的概率+随机选出两个C的概率+……+随机选出两个Z的概率。对英语而言,根据上述的频率表,我们可以计算出英语文本的重合指数为:
P(A)^2 + P(B)2+……+P(Z)2 = 0.65
利用重合指数推测密钥长度的原理在于,对于一个由凯撒密码加密的序列,由于所有字母的位移程度相同,所以密文的重合指数应等于原文语言的重合指数。据此,我们可以逐一计算不同密钥长度下的重合指数,当重合指数接近期望的0.65时,我们就可以推测这是我们所要找的密钥长度。
举例来说,对密文ABCDEABCDEABCDEABC
首先测试密钥长度=1,对密文ABCDEABCDEABCDEABC统计每个字符出现的次数:
A: 4 B: 4 C: 4 D:3 E:3
那么对于该序列的重合指数就为:(4/18)^2 + (4/18)^2 + (4/18)^2 +(3/18)^2 +(3/18)^2 != 0.65
然后测试密钥长度=2,将密文ABCDEABCDEABCDEABC分解为两组:
组1:A C E B D A C E B
组2:B D A C E B D A C
我们知道如果密钥长度真的是2,那么组1,组2都是一个凯撒密码。对组1组2分别计算重合指数。
如果组1的重合指数接近0.65,组2的重合指数也接近0.65,那么基本可以断定密钥长度为2。
在知道了密钥长度n以后,就可将密文分解为n组,每一组都是一个凯撒密码,然后对每一组用字母频度分析进行解密,和在一起就能成功解密凯撒密码。
上文已经说到,自然语言的字母频度是一定的。字母频度分析就是将密文的字母频度和自然语言的自然频度排序对比,从而找出可能的原文。
附录
参考链接:
维吉尼亚密码
简单的加密算法——维吉尼亚密码
出自-简单的加密算法——维吉尼亚密码 ↩︎