移动网络安全课_期末思考题(wbd班)
1、列举你所知道的密码体制类型,描述各自相应例子,阐述你如何理解密码技术在现实生活中的作用。
解:一般分为单钥密码体制和双钥密码体制,单钥密码体制特点是加密解密都用同一个密钥,优点是安全性高,加密速度快;缺点:1)随着网络规模的扩大,密钥的管理成为一个难点;2)无法解决消息确认问题;3)缺乏自动检测密钥泄露的能力。双钥密码体制特点是加密、解密分别使用一个密钥,优点:可以拥有数字签名等新功能。缺点:双钥密码算法一般比较复杂,加解密速度慢。
举例:单钥密码体制一般指对称分组加密,有DES算法、AES算法、RC5、RC6等;双钥密码体制一般用于非对称加密,如RSA加密、数字签名算法、ElGamal算法等。在现实生活中,密码加密是随处可见的,如微信,登陆时采用的是RSA加密,用户用公钥加密明文(内含用户名、密码、Aes随机密钥)然后发送到腾讯服务器,服务器用私钥解密后验证成功后,则用里面的Aes加密验证明文并返回给用户,用户用AES密钥解密后,之后通信一直用Aes加密。
以上例子说明微信其实是综合使用RSA与AES两种加密算法。在现实生活中,各种博客账号、社交账号登陆信息都得用密码技术加密才能发送,否则很容易被人窃取到,从而泄露了隐私。
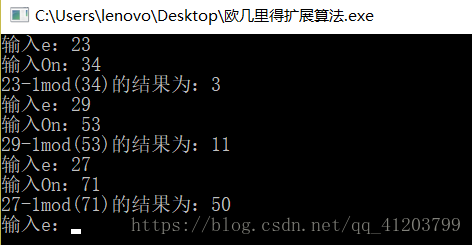
2、求23-1 mod 34、29-1 mod 53、27-1 mod 71。
解:(1)欧几里扩展算法数学解法(计算x -1mod y通过分解得到形如a*x+b*y=1的式子,解即是a):
23-1 mod 34 29-1 mod 53 27-1 mod 71
解:34=23*1+11 解:53=29*1+24 解:71=27*2+17
23=11*2+1 29=24*1+5 27=17*1+10
=>1=23-2*11=23-2*(34-23) 24=5*5-1 17=10*1+7
=>1=-2*34+3*23 =>1=5*(29-24)-24 10=7*1+3
所以求得解为3 =>1=5*29-6*(53-29) 7=3*2+1
=>1=29*11-6*53 =>1=7-3*2=7-2*(10-7)=-2*10+3*7
所以求得解为11 =>-2*10+3*(17-10)=-5*10+3*17
=>-5*(27-17)+3*17=-5*27+8*17
=>-5*27+8*(71-2*27)=8*71-21*27
由于解为负数(-21),如果要求最小正整数解,则两边取反再加2得=>1=-19*71+50*27 所以求得解为50
(2)编程解法
#include
#include
#include
using namespace std;
//e*x+On*y=1 求 a mod b的乘法逆次元
int exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{ //1的情况
x=1;
y=0;
return a;
}
int r=exgcd(b, a%b, x, y);
int t=y;
y=x-(a/b)*y; //2的情况
x=t;
return r;
}
//本来直接调用exgcd即可求解乘法逆次元,但有时会出现负数,所以精益求精,使用cal()函数
int cal(int a,int n)
{
int x,y;
int gcd=exgcd(a, n, x, y);
if(1%gcd!=0)
{
return -1;
}
x*=1/gcd;
n=abs(n);
int ans=x%n;
if(ans<=0)
ans+=n;
return ans;
}
int main(){
int On,e,d;
while(1){
cout<<"输入e:";
cin>>e;
cout<<"输入On:";
cin>>On;
d=cal(e,On);
cout< 编译结果
3、求下列方程组的最小解。
解:要得到x=m mod34 x=m mod 53 x=m mod 71(余式组求解)
则有x=34*a+2=53*b+3=71*c+2 最小解为:a=71 b=2413/53 c=34 使b为整数时 m=26556
所以x=26556 mod 34
x=26556 mod 53 ==>26556mod (34*53*71) 即x=26556mod 127942(求解结果)
x=26556 mod 71
编程解法:
#include
using namespace std;
int main(){
int x=1;
while(1){
if(x%34==2 && x%53==3 && x%71==2){
cout< return 0;
}
x++;
}
}
结果:
4、请各给出有限群、无限群、有限环、无限环、有限域、无限域的一个例子!
构成一个群的条件是,做以下一种代数运算,如加法运算,而满足条件
有限群:一个含有限个元素的群,如非空集合G={0,1,2,3,4,5,6,7,8,9,10},在mod11的情况下做加法运算,构成一个群且是交换群,满足以下情况:
(1) 封闭性。对任意a,b属于G,恒有a+b(mod11)属于G。例如8+9(mod11)=6仍属于G集合
(2) 结合律成立。对任意a、b、c属于G,有(a+b)+c=a+(b+c)
(3) G中有一恒等元e存在,对任意a属于G,有e属于G,使a+e=e+a=a.在该集合G中,e=0时满足条件
(4) 对于任意a属于G,存在a的逆次元a-1属于G,使得a+a-1=a-1+a=e。例如7在集合中逆次元为4,因为7+4(mod11)=0
无限群:例子:f(n)=n,n=0,1,2,..n为无限群。自证。
有限域:p是素数时,可证F{0,1,2,…,p-1},在mod p意义下,关于求和运算“+”,及乘积“*”,构成了域.且F域的元素数目有限时称为有限域.故集合G={0,1,2,3,4,5,6}mod7做加运算和乘运算下可构成有限域。
无限域:在满足环的条件同时满足乘法逆元则为域,事实上有理数集合、实数集合等都是无限域;如f(x)=x,x属于R
有限环:由于群包含于环,环包含于域,故集合G={0,1,2,3,4,5,6}mod7做加运算和乘运算下可构成有限环。事实上,整数{0,1,2,...n-1}的集合Zn加上模n的算法运算可构成一个交换环。
无限环:环在满足群的条件下,同时满足乘法封闭性(a,b属于R,则ab也属于R)、结合律以及分配律。其实,实数上所有n阶矩阵的结合关于加法和乘法构成一个环,则f(n)=0,1,2,3...n也构成一个无限环
5、构造具有8个元素的有限域:给出域的各个元素,描述清楚域的加法运算和乘法运算。
构造GF(2^3)的有限域{0,1,2,3,4,5,6,7},由于用一个0-2^n-1的集合,单纯地用模运算去构建加法运算和乘法运算,是构成不了域的,所以我们需要用到多项式模运算,即GF(2^3)有8项多项式:0,1,x,x+1,x^2,x^2+1,x^2+x,x^2+x+1具体讲解烦请看《密码编码学与网络安全 第六版》83页4.7.2章节。
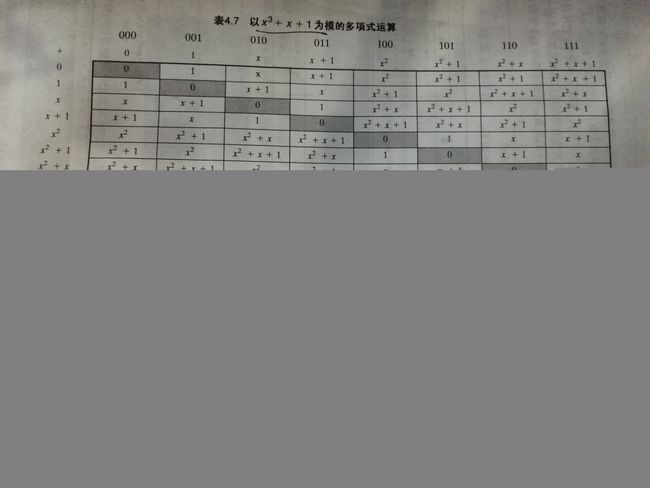
以x^3+x+1为模进行多项式运算
算得加法运算如下:
+ |
000(0) |
001 (1) |
010(2) |
011(3) |
100(4) |
101(5) |
110(6) |
111(7) |
000 (0) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
001(1) |
1 |
0 |
3 |
2 |
5 |
4 |
7 |
6 |
010(2) |
2 |
3 |
1 |
0 |
7 |
6 |
5 |
4 |
011(3) |
3 |
2 |
1 |
0 |
7 |
6 |
5 |
4 |
100(4) |
4 |
5 |
6 |
7 |
0 |
1 |
2 |
3 |
101(5) |
5 |
4 |
7 |
6 |
1 |
0 |
3 |
2 |
110(6) |
6 |
7 |
4 |
5 |
2 |
3 |
0 |
1 |
111(7) |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
乘法运算:
x |
000(0) |
001 (1) |
010(2) |
011(3) |
100(4) |
101(5) |
110(6) |
111(7) |
000 (0) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
001(1) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
010(2) |
0 |
2 |
4 |
6 |
3 |
1 |
7 |
5 |
011(3) |
0 |
3 |
6 |
5 |
7 |
4 |
1 |
2 |
100(4) |
0 |
4 |
3 |
7 |
6 |
2 |
5 |
1 |
101(5) |
0 |
5 |
1 |
4 |
2 |
7 |
3 |
6 |
110(6) |
0 |
6 |
7 |
1 |
5 |
3 |
2 |
4 |
111(7) |
0 |
7 |
5 |
2 |
1 |
6 |
4 |
3 |
6、证明n维实数向量的集合在普通向量加法下构成交换/Abel群。
证明:在加法运算下,n维实数向量形如{0,1,2,...n-1}mod n是一个群(4题证明过),同时均满足a+b=b+a,即交换律成立,故可构成交换群。
7、请各给出单字母单表代换、单字母多表代换、多字母单表代换、多字母多表代换、置换密码的一个例子。
1) 单字母单表代换:任何密文是对相应明文的各组信息单元使用同一个代换表进行替换而得到的
例子:如明密字母变换公式: c = m+k (mod 26),其中k为移动的位数且k=1,2,3,...25
当k=7时,代换表为:

2) 单字母多表代换:密文是依次对相应明文的各组信息单元使用有限个周期性重复的或无限多的固定代换表进行替换而得到的
如Vigenere密码,利用Vigenere方阵进行加密:用明文字母在Vigenere方阵中的列和密钥在Vigenere 方阵中的行的交叉点处的字母来代换明文字母
设明文m=(m1,m2..mn),密钥k=(k1,k2..kn),则密文c=(c1,c2..cn)为c=Ek(m)
例子:设明文为this is secure,密文为cipher,则密文为?
解:this is secure
Ciph er cipher
根据Vigenere方阵表

算得密文为vpxz mj zitwzt
3) 多字母单表代换:明文的一个或多个字符用相应的多个密文字符代换,如Playfair,加密方法如下:首先选择一个密钥单词(称为 pair)(字母不重复,且都为小写字母),然后与字母表中其他字母一起填入至一个 5x5的方阵中,填入方法如下:1.首先按行填入密钥串。2.紧接其后,按字母序按行填入不在密钥串中的字母。
加密规则:

Playfair加密实例:若输入:youandme(密钥pair) 明文:welcometohangzhou
密钥形成的正方形如下:
y o u a n
d m e b c
f g h i j
k l p q r
s t v w x
在正方形中可以找到以第一对字母 we为顶点的矩形,对应另一对顶点字母为 vb,因此加密后为vb,同理可找到与字母对 lc,et,oh,ho对应的顶点字母对。而字母对 om位于上述正方形中的同一列,所以直接以颠倒这两个字母来加密,即为 mo,字母对an 同理。字母对 gz中的z 不在上述正方形中,因此原样放到加密串中。最后剩一个字母 u也原样输出。
因此输出的结果为:
vbrmmomvugnagzguu
4) 多字母多表代换
Hill加密:

5) 置换密码:

举例:

9、说明分组密码有哪些运行模式,从加密单位(比特/分组)、密文重复、错误传播、消息填充和运算的并行性等角度进行比较分析。
|
ECB |
CBC |
CFB |
OFB |
CTR |
全称 |
电子密码本 |
密文分组链接 |
密文反馈 |
输出反馈 |
计数器 |
加密单位 |
分组 |
分组 |
比特流和分组 |
比特流 |
分组 |
密文重复 |
有重复 |
无重复 |
无重复 |
无重复 |
无重复 |
错误传播 |
影响所有明文分组 |
影响本次和下次操作 |
明文的相应位以及下一个分组 |
明文的相应位 |
明文的相应位 |
串/并行 |
并行 |
加密串行,解密并行 |
加密串行,解密并行 |
串行 |
并行 |
填充与否 |
需要填充 |
需要填充 |
需要填充 |
无需填充 |
无需填充 |
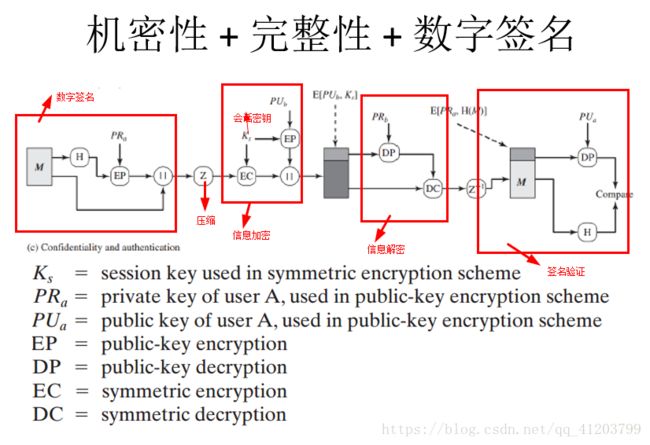
10、说明对称密码、公钥密码在实际应用(如PGP邮件系统或EFS文件加密系统)中的应用方式。
解:PGP在对哈希摘要以及会话密钥的加密解密时用到对称加密;其次RSA公钥加密体制,数字签名公钥用于解密,信息加密时公钥用于加密。
PGP发送邮件的步骤如下:
步骤一:数字签名。首先用哈希函数处理消息得到摘要,再利用私钥环机制获取私钥去RSA加密摘要,然后传输加密摘要和明文消息。
步骤二:信息压缩。为了减少邮件传输和文件存储过程节约空间,对信息进行压缩后再发送。
步骤三:信息加密(该过程用到对称加密以及公钥加密)。RNG产生一个会话密钥并利用会话密钥对压缩的信息进行对称加密(一般为3DES或IDAE),然后通过公钥环的公钥对会话密钥进行RSA加密,然后将对称加密的信息以及RSA公钥加密的会话密钥密文一同发送给接收方。
PGP接收邮件步骤如下:
步骤一:解压接收到的信息,获得被加密的密文和被加密的会话密钥。
步骤二:信息解密(该过程用到对称解密):用私钥环的RSA私钥去解密会话密钥,然后用会话密钥去对称解密密文
步骤三:签名验证:将解密的明文分解成已加密的哈希摘要和未被加密过的明文,用公钥环的公钥解密哈希摘要(该过程用到公钥解密),并与明文进行比较,如果一致说明数据未被篡改,验证成功
附图一张:
PS:仅作参考,不一定完全正确