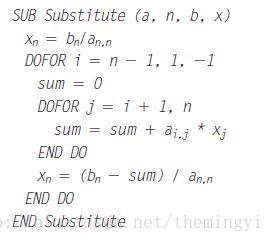部分交换主元的高斯消去法

伪代码（pseudocode）

程序：

function Gauss(a,b,tol)
if nargin==2%
    tol = 1e-4;
end
n = size(a,1);%dimention
s = zeros(n,1);%initialize & save maximum value of each row

%% Select  maximum value of each row
for i = 1 : n
    s(i) = abs(a(i,1));
    for j = 2 : n
        if abs(a(i,j)) > s(i)
            s(i) = abs(a(i,j));
        end
    end
end
%% Call sub function 
[a,b,er] = Elimization(a,b,s,n,tol);
%% Determine the solution
if er ~= -1
    X = Substitude(a,b,n);
end
disp(X);
%%Writed by 王明文 2017/10/6

function [a,b,er]  = Elimization(a,b,s,n,tol)
%Illustration: forward elimination
er = 0;
for k = 1 : n-1
    [a,b,s] = Pivot(a,b,s,n,k);% call Sub function to implement Gauss Elimization with partial pivoting
    if abs(a(k,k) / s(k) ) < tol
        er = -1;%flag 
        %When choose the main element or the coefficient of 
        % abs(a(n,n)) < tol, then assign er to -1
        break;
    end
    for i = k+1:n
        factor = a(i,k) / a(k,k);
        for j = k+1:n
            a(i,j) = a(i,j) - factor*a(k,j);
        end
        b(i) = b(i) - factor*b(k);
    end
end
if abs(a(n,n)/s(n)) < tol
    er = -1;
end
%%Writed by 王明文 2017/10/6

function [A,b,s] = Pivot(a,b,s,n,k)
%Illustration :  implement Gauss Elimization with partial pivoting
p = k;%Record line number 
big = abs(a(k,k) / s(k));%Record main element
for ii = k+1 : n%Operating row
    dummy = abs(a(ii,k) / s(ii));
    if dummy > big
        big = dummy;
        p = ii;
    end
end

if p ~= k
    for jj = k : n%Operating column
            dummy = a(p,jj);
            a(p,jj) = a(k,jj);
            a(k,jj) = dummy;
    end
    dummy = b(p);
    b(p) = b(k);
    b(k) = dummy;
    dummy = s(p);
    s(p) = s(k);
    s(k) = dummy;    
end
A = a;
%%Writed by 王明文 2017/10/6

function X = Substitude(a,b,n)
%Illustration: back substitution
x = zeros(n,1);%initialize & save solution
x(n) = b(n) / a(n,n);
% for i = n-1 :-1 :1
%     sum = 0;
%     for j = i+1:n
%         sum = sum - a(i,j)*x(j);
%     end
%     x(i) = (b(n) - sum) / a(n,n);
% end

for i = n-1 : -1 : 1
    sum = b(i);
    for j = i+1 : n
        sum = sum - a(i,j) * x(j);
    end
    x(i) = sum / a(i,i);
end
X = x;
%%Writed by 王明文 2017/10/6

调用：