底层实现数据结构:线段树
目录
- 什么时候使用线段树
- 线段树的创建
- 源码详解
- 存储结构
- 建树
- 查询
- 更新
- merge 的创建
- 完整源码
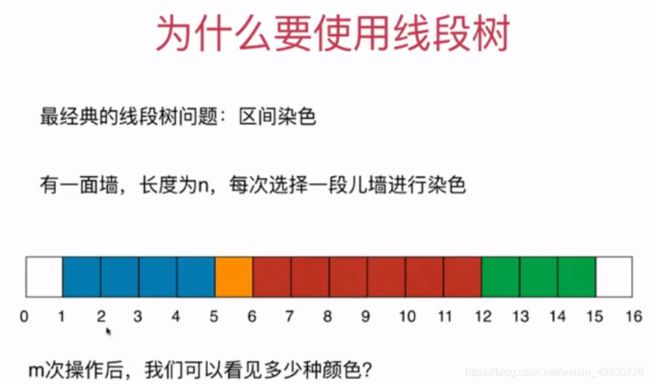
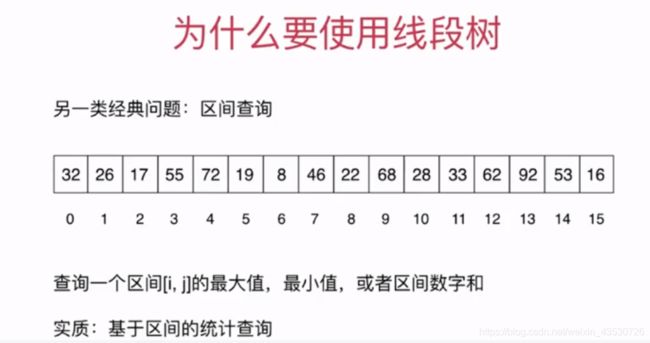
什么时候使用线段树?
总的来说,一个区间如果会发生动态地变化,可以用线段树

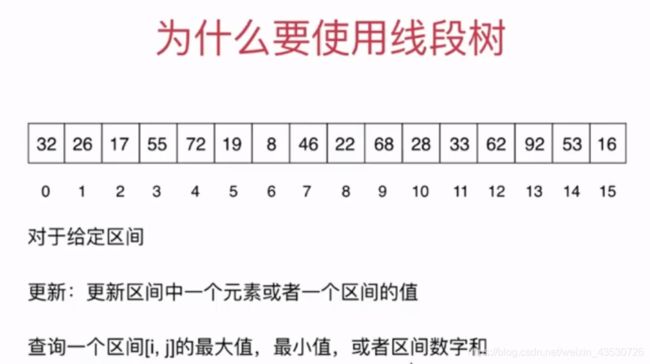
具体例子:
我们现在要从数组 arr[0…n-1] 中查找某个数组某个区间内的最小值,其中数组大小固定,但是数组中的元素的值可以随时更新。
那么我们可以根据这个问题构造如下的二叉树:
- 叶子节点是原始组数arr中的元素
- 非叶子节点代表它的所有子孙叶子节点所在区间的最小值
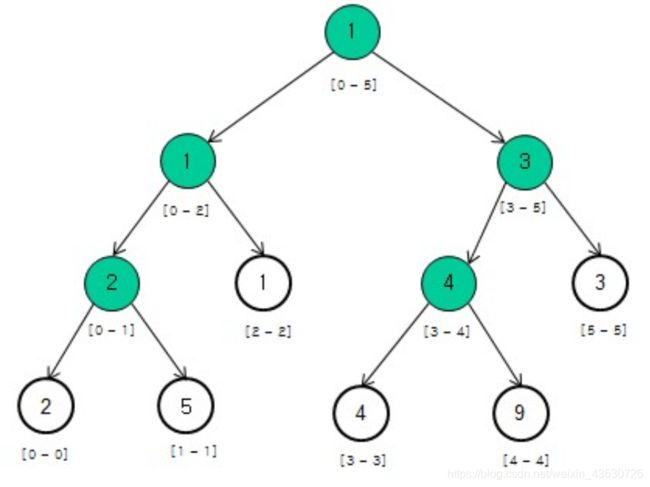
例如对于数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树(背景为白色表示叶子节点,非叶子节点的值是其对应数组区间内的最小值,例如根节点表示数组区间arr[0…5]内的最小值是1):
-------------------------------------------------------------------------------- 回到目录
线段树的创建
1、线段树的创建是一个递归和类似二分的过程,首先我们将我们的整个区间(也就是整个数组)作为整个线段的根结点;
2、然后我们将区间分为两半,[L,m] 和 [m+1,R],然后递归的去创建各自的线段树;
3、边界条件是直到我们的区间中只有一个元素的时候,我们就使用这个元素建立出叶子结点;
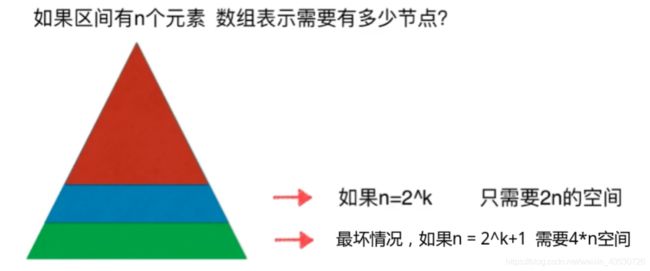
创建需要多少空间?
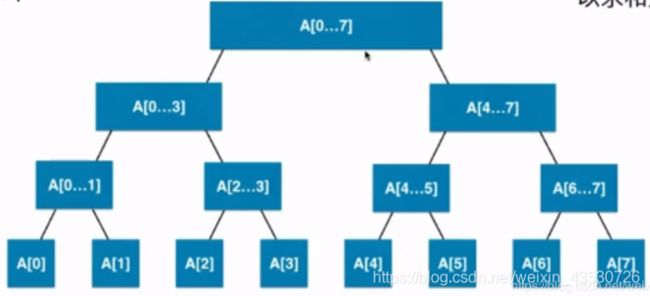
我们保存树的结构是类似和堆一样的使用数组来保存,使用下标来对应左右孩子。
抽象图示:
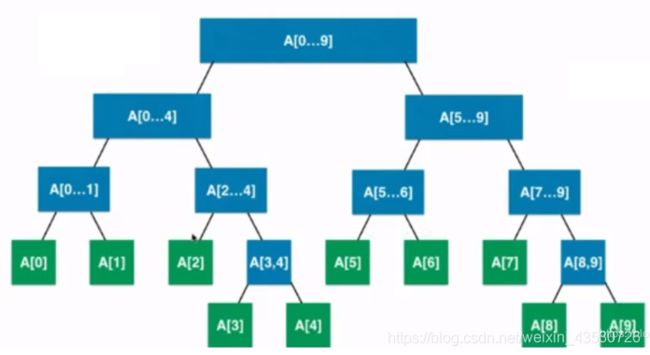
具体图示:
当区间的划分的个数是奇数个的时候,那么左右两边的个数不同,下面的图是左边(0…1)(5…6)比右边(2…4)(7…9)的少一个。
-------------------------------------------------------------------------------- 回到目录
源码详解
存储结构
public class SegmentTree<E> {
//这个Merger和compareTO类型差不多,具体逻辑自己定义
private interface Merger<E>{
E merge(E a,E b);
}
private E[] tree;
private E[] data;
private Merger<E> merger;
public SegmentTree(E[] arr,Merger<E> merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
for(int i = 0; i < arr.length; i++)
data[i] = arr[i];
tree = (E[]) new Object[4 * arr.length]; //最多需要4 * n
buildSegmentTree(0, 0, arr.length - 1);
}
}
- 接口 Merger 用于查询区间和,查询最大值,查询最小值。
- data 存原始数据。
- tree 用于描述树的结构,大小为 4 * arr.length。
- buildSegmentTree() 函数是创建线段树。
-------------------------------------------------------------------------------- 回到目录
建树
先建好叶子节点再往上建区间节点。
public void buildSegmentTree(int treeIndex,int L,int R){
//区间为1
if(L == R){ //叶子结点,直接创建赋值
tree[treeIndex] = data[L];
return;
}
int treeL = treeIndex * 2 + 1; //左孩子对应的下标
int treeR = treeIndex * 2 + 2; //右孩子下标
int m = L + (R - L) / 2; //(L + R)/ 2 防溢出写法
// 先把左右子树建好
//[0,4] ---> [0,2](3), [2,4](2)
buildSegmentTree(treeL,L,m);
buildSegmentTree(treeR,m+1,R);
//然后我再把左右子树合并(sum | max | min)
//不能使用 + 的原因是类型 E 不一定定义了加法,所以我们不能保证这个加法一定是合法的
tree[treeIndex] = merger.merge(tree[treeL],tree[treeR]);
}
- merge 的具体用法在创建实例的时候声明。(在main函数里写具体逻辑)
-------------------------------------------------------------------------------- 回到目录
查询
假设查询的区间为[qL,qR],分为三种情况:
- qR <= m,说明我们要去左边的区间查询;
- qL > m ,说明我们要去右边的区间查询;
- 其他情况,说明左右两边都要查询,查完之后,记得合并;
//查询[qL,qR]的 sum | max | min
public E query(int qL,int qR){
//这里可以throw new illegalArgumentException,而不return null
if(qL < 0 || qL >= data.length || qR < 0 || qR >= data.length || qL > qR)
return null;
return query(0,0,data.length - 1,qL,qR);
}
//在以treeindex为根的线段树[l...r]的范围里,搜索区间[ql...qr]的值
private E query(int treeIndex,int L,int R,int qL,int qR){
if(L == qL && R == qR){
return tree[treeIndex];
}
int m = L + (R - L) / 2;
int treeL = treeIndex * 2 + 1;
int treeR = treeIndex * 2 + 2;
if(qR <= m){ //和右区间没关系 ,直接去左边查找 [0,4] qR <= 2 [0,2]之间查找
return query(treeL,L,m,qL,qR);
}else if(qL > m ) {//和左区间没有关系,直接去右边查找 [0,4] qL > 2 --> [3,4]
return query(treeR,m+1,R,qL,qR);
}else { //在两边都有,查询的结果 合并
return merger.merge(query(treeL,L,m,qL,m), //注意是查询 [qL,m]
query(treeR,m+1,R,m+1,qR)); //查询[m+1,qR]
}
}
-------------------------------------------------------------------------------- 回到目录
更新
先修改数组的值,然后递归的查找到叶子,然后沿途修改树中结点的值。
public void update(int index,E e){
if(index < 0 || index >= data.length )return;
data[index] = e; //首先修改data
update(0,0,data.length-1,index,e);
}
private void update(int treeIndex,int L,int R,int index,E e){
if(L == R){
tree[treeIndex] = e;
return;
}
int m = L + (R - L ) / 2;
int treeL = 2 * treeIndex + 1;
int treeR = 2 * treeIndex + 2;
if(index <= m){ //左边
update(treeL,L,m,index,e);
}else {
update(treeR,m+1,R,index,e);
}
tree[treeIndex] = merger.merge(tree[treeL],tree[treeR]); //更新完左右子树之后,自己受到影响,重新更新和
}
-------------------------------------------------------------------------------- 回到目录
main 函数中 merge 的创建:
以下是求和的 merge,当然也可以写成找最大最小值的 merge,具体使用看自己的需求。
//对于只使用一次的类我们可以使用匿名类
//逻辑也可以写成 SegmentTreesegmentTree = new SegmentTree<>(arr, (a, b) -> a + b);
SegmentTree<Integer>segmentTree = new SegmentTree<Integer>(arr, new Merger<Integer>() {
@Override
public Integer merge(Integer a, Integer b) {
return a + b;
}
});
-------------------------------------------------------------------------------- 回到目录
完整源码
import java.util.Arrays;
public class SegmentTree<E> {
//操作的方式: 求和 | 查询最大值 | 最小值
private interface Merger<E>{
E merge(E a,E b);
}
private E[] tree;
private E[] data;
private Merger<E> merger;
public SegmentTree(E[] arr,Merger<E> merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
for(int i = 0; i < arr.length; i++) data[i] = arr[i];
tree = (E[]) new Object[4 * arr.length]; //最多需要4 * n
buildSegmentTree(0, 0, arr.length - 1);
}
// tree是树的结构(类似堆的存储)
public void buildSegmentTree(int treeIndex,int L,int R){
if( L == R){
tree[treeIndex] = data[L];
return;
}
int treeL = treeIndex * 2 + 1;
int treeR = treeIndex * 2 + 2;
int m = L + (R - L) / 2;
// 先把左右子树建好
//[0,4] ---> [0,2](3), [2,4](2)
buildSegmentTree(treeL,L,m);
buildSegmentTree(treeR,m+1,R);
//然后我再把左右子树合并(sum | max | min)
tree[treeIndex] = merger.merge(tree[treeL],tree[treeR]);
}
//查询[qL,qR]的 sum | max | min
public E query(int qL,int qR){
if(qL < 0 || qL >= data.length || qR < 0 || qR >= data.length || qL > qR)return null;
return query(0,0,data.length - 1,qL,qR);
}
// [treeIndex,L,R]表示的是结点为treeIndex的树的左右区间范围(arr的下标)
private E query(int treeIndex,int L,int R,int qL,int qR){
if(L == qL && R == qR){
return tree[treeIndex];
}
int m = L + (R - L) / 2;
int treeL = treeIndex * 2 + 1;
int treeR = treeIndex * 2 + 2;
if(qR <= m){ //和右区间没关系 ,直接去左边查找 [0,4] qR <= 2 [0,2]之间查找
return query(treeL,L,m,qL,qR);
}else if(qL > m ) {//和左区间没有关系,直接去右边查找 [0,4] qL > 2 --> [3,4]
return query(treeR,m+1,R,qL,qR);
}else { //在两边都有,查询的结果 合并
return merger.merge(query(treeL,L,m,qL,m), //注意是查询 [qL,m]
query(treeR,m+1,R,m+1,qR)); //查询[m+1,qR]
}
}
public void update(int index,E e){
if(index < 0 || index >= data.length )return;
data[index] = e; //首先修改data
update(0,0,data.length-1,index,e);
}
private void update(int treeIndex,int L,int R,int index,E e){
if(L == R){
tree[treeIndex] = e;
return;
}
int m = L + (R - L ) / 2;
int treeL = 2 * treeIndex + 1;
int treeR = 2 * treeIndex + 2;
if(index <= m){ //左边
update(treeL,L,m,index,e);
}else {
update(treeR,m+1,R,index,e);
}
tree[treeIndex] = merger.merge(tree[treeL],tree[treeR]); //更新完左右子树之后,自己受到影响,重新更新和
}
public static void main(String[] args) {
int[] nums = {-2, 0, 3, -5, 2, -1};
//int型数组不能直接转换为Integer型数组,需要手动装箱
Integer[] arr = new Integer[nums.length];
for(int i = 0; i < nums.length; i++) arr[i] = nums[i];
//使用匿名类
//逻辑也可以写成 (a, b) -> a + b
SegmentTree<Integer>segmentTree = new SegmentTree<Integer>(arr, new Merger<Integer>() {
@Override
public Integer merge(Integer a, Integer b) {
return a + b;
}
});
System.out.println(segmentTree.query(0, 2));
System.out.println(Arrays.toString(segmentTree.tree));
segmentTree.update(1,2);
System.out.println(segmentTree.query(0, 2));
System.out.println(Arrays.toString(segmentTree.tree));
}
}
-------------------------------------------------------------------------------- 回到目录