2020五一建模:C题 饲料混合加工问题 题解

我觉得蒸米的时候米与水的配比是一个NP-hard问题

问题一题解

分析

问题1研究16个加工原料两两之间的亲缘值，并进行统计分析。根据题目所给的16个加工原料的基因序列信息，进行两两比对，若两个加工原料有N个相同位点的基因序列标记相同，就认为这两个加工原料的亲缘值为N。用python进行编程编写计算亲缘度的函数，遍历所有原料两两之间的组合，统计他们的亲缘值并记录在一个16*16的方阵中，并做统计学分析。

求解

首先根据题目所给亲缘值定义:两个加工原料如果有 N 个相同位点的基 因序列标记相同，就认为这两个加工原料的亲缘值为 N(如果 N 大于 0，则说明 这两种加工原料之间具有亲缘关系)。由于两两原料之间没有先后顺序关系，故利用排列组合知识对每一种原料组合的亲缘度进行计算求解。

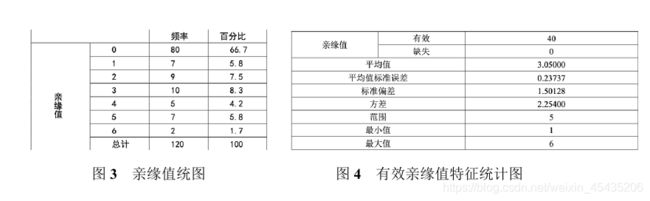
根据题目所给表 1 各加工原料的品种代码、总重量、效能率和基因序列标记，使用python编写程序计算得到一个16*16的方阵，对应任意两个加工原料间的亲缘度，并对数据进行处理。处理结果如图1，数据分析结果如图2。

根据图3、4可知，16种加工原料两两组合方式有120种，其中具有亲缘关系的加工原料两两组合种类有40种，亲缘值最小为1，最大为6，均值为3.0500。

问题二题解

分析

问题 2 要求将 16 种加工原料全部放入 9 个加工窖中进行加工，建立数学模型，求出能得出饲料质量最高的混合并给出每个加工包的亲缘度。仅从亲缘度角度考虑混合加工饲料的质量，亲缘度越高，饲料质量就越高，则问题二最终目标转化为求取亲缘度最优值问题，并给出饲料质量最高的混合方案。

将16种加工原料进行混合投放到9个加工窖中进行加工，根据亲缘关系进行组合，构成一个排列组合问题，但由于直接对所有组合求取全局最优解所需要时间代价太大，因此使用随机选取的方式来不断选取局部最大值，在局部优化的基础上找到近似的全局最优解。同时在选择方案时，需要考虑加工窖的质量范围约束。

求解

问题2要求将16种原料分别放入9个加工窖中进行加工，求出饲料质量最高的混合方案并给出每个加工包的亲缘度。问题二的假设是饲料质量仅取决于亲缘度，所以我们的优化目标就是使得不同的满足条件的分配，其亲缘度最大。

将16种原料分别放入9个加工窖中进行加工，这样的分配方案有很多种，每种方案的加工包亲缘度也不同，分配方案具有随机性质。又因为直接进行全局考虑十分耗时，代码的运行时间超出实际承受范围。因此我们在最终处理的循环中可以考虑使用随机选取的方式来不断选取局部最大值，在局部优化的基础上找到近似的全局最优解。

目标函数的建立:

最终的优化对象为总亲缘值，即
$$K=\frac{{\sum }_{i=1}^9{K}_i\times W_i}{{\sum }_{i=1}^9{W}_i}$$
其中，$W_i$表示第i个加工包的加工重量
$$W_i=\sum _{j=1}^{16}{w}_{ij}\times E_j$$
混合的方案则为$w_{ij}$
原料总重量：
$$W{M}_j=\sum _{i=1}^9{w}_{ij}$$
加工包总重量：
$$W{C}_i=\sum _{j=1}^{16}{w}_{ij}$$
加工包总重量要符合加工窖标准：
$$P_{im}\le W{C}_i\le P_{hm}$$
n=1时，加工窖只有一种原料，重量要超过500kg：
$$W{C}_i\ge 500,n=1$$
j=10时，原料10必须混合才能加工：
$$W{C}_i-w_{ij}>0,j=10,n\ge 2$$
只有一种原料时亲缘值为10：
$$K_i=10,n=1$$
加工包必须任意两个原料亲缘值不为0：
$$C_i\in B$$
根据上述条件建立问题2的优化模型，即：
$$maxK=\frac{{\sum }_{i=1}^9{K}_i\times W_i}{{\sum }_{i=1}^9{W}_i}$$
$$s.t.\{\begin{array}{rl}{W}_i& =\sum _{j=1}^{16}{w}_{ij}\times E_j\\ W{C}_i& =\sum _{j=1}^{16}{w}_{ij}\\ P_{im}& \le W{C}_i\le P_{hm}\\ W{C}_i& \ge 500,n=1\\ W{C}_i& -w_{ij}>0,j=10,n\ge 2\\ K_i& =10,n=1\\ C_i& \in B\end{array}$$
模型求解：

1.$w_{ij}$分配的求解过程：考虑不同混合方案对$w_{ij}$分配不同，每种个原料都可以拆分，因此以每一种原料重量的1/10为步长进行循环迭代，结合随机数的选取，不停的考虑不同情况的分配，直至求到局部最优解。

2.根据1求解后的结果，读取亲缘值表，计算出各加工窖的亲缘值，最终求得总亲缘值。

求解结果：

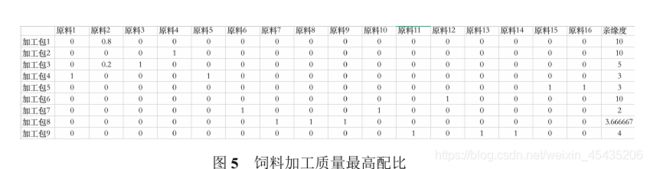
模型优化求解后，可得按权重平均后的亲缘度为4.845937217，此时的饲料加工配比图如下图所示，即饲料加工质量最高的配比情况。经检验该配比满足所有的约束条件。

问题三题解

分析

问题 3 是将16 个加工原料进行混合全部放入9个加工窖中，求出平均效能率超过 80%的加工包数量最多的混合方案并给出每个加工包的效能率。问题三的求解与问题二类似，可以在问题二的基础上改变目标函数和约束条件，寻找加工原料的最优混合方案。

问题中包含16种元素，9个加工窖。假设在加工原料混合方案确定后，将混合原料投放到9个加工窖形成 9 个加工包，每一个加工包都有一个效能率。 因此需建立起优化目标函数，在问题2的基础之上结合题目所给的约束条件进行穷举和筛选，获得最优解，给出方案配比完成表3。

求解

问题 3 是将 16 个加工原料进行混合全部放入 9 个加工窖中，求出平均效能 率超过 80%的加工包数量最多的混合方案并给出每个加工包的效能率。对于问题3，可以建立在问题2的约束条件下，改变部分约束条件和优化目标进行建模求解。

假设每种加工原料的能耗率不随时间变化，且加工包的能耗率不受加工窖影响，只和原料的能耗率有关。因此，单个加工包的能耗率只与其加工窖中的加工原料及其质量有关。据此，根据题目所给的每种原料的能耗率建立优化目标函数，确定约束条件进行求解，并将最终结果填入附表3。

确立目标函数：

$E{C}_i$表示第i个加工包中原料的平均能耗率，则
$$E{C}_i=\frac{W_i}{W{C}_i}=\frac{{\sum }_{j=1}^{16}{w}_{ij}\ast E_j}{{\sum }_{j=1}^{16}{w}_{ij}}$$

$E_t$表示平均能耗率大于0.8的加工包数量，令$g(E{C}_i)$为
$$g=\{\begin{array}{rl}1& ,E{C}_i\ge 0.8\\ 0& ,E{C}_i\le 0.8\end{array}$$

故目标函数为
$$max{E}_t=\sum _{i=1}^{9}g(E{C}_i)$$

对于约束条件，基本与问题2类似，即
$$s.t.\{\begin{array}{rl}{W}_i& =\sum _{j=1}^{16}{w}_{ij}\times E_j\\ W{C}_i& =\sum _{j=1}^{16}{w}_{ij}\\ P_{im}& \le W{C}_i\le P_{hm}\\ W{C}_i& \ge 500,n=1\\ W{C}_i& -w_{ij}>0,j=10,n\ge 2\\ K_i& =10,n=1\\ C_i& \in B\end{array}$$

模型求解：

1.先根据所给效能率信息，同时筛选出本身效能率超过0.8和低于0.8的原料。对低于0.8比较多的原料来说，想要达到超过0.8的效能率，必须搭配一个效能率超过0.8的原料，而本题的原料2，质量大并且效能率低，想要最终超过0.8必须搭配很多高效能的原料，无疑是一种浪费。因此优化考虑增加条件，尽可能把原料2单独分配
。

2.对满足条件的情况分别用不同的搜索初值进行搜索遍历，并计算最终效能率超过0.8的个数
。

3.将上述局部最优值与第2问结果比对，取出更大的那一个。

根据模型进行求解计算，得到优化结果，平均能耗率大于0.8的加工包有7个，将题目中所给的表3补充完整，结果如图6：

问题四题解

分析

问题4要求在允许部分加工窖不生产的情况下，满足给定的两个条件，一个是成本尽量低，另一个是平均效能率超过80%的加工包尽量多。取消一次性加工的限制。

根据题目要求，该问题属于双目标优化问题，各种约束条件下设计出一个可以使得成本最小化、平均效能率超过80%的加工包尽量多的混合方案。我们将双目标优化问题通过加权转化为单目标优化问题。从成本以及效能率两个角度进行考虑，将复杂的任务预定规则转化为约束条件。在考虑加工成本最低时，我们发现加工窖的容量越大， 加工成本越低，因此优先使用加工容量较大的加工窖进行加工。我们按照加工要求，设定约束条件，求解双目标优化模型。

求解

问题4要求如果饲料加工厂允许部分加工窖不生产，建立数学模型，给出混合加工方案，用尽量低的加工成本完成整个加工任务，同时要求平均能耗率超过80%的加工包尽量的多。因此这是一个双目标优化问题，一个是成本尽可能低，第二个是平均能耗率超过80%的加工包尽量的多。经计算我们得知所有加工窖的最大加工能力是8100kg，所需要加工的原料一共为6000kg，可以得知最多停用3个加工窖，即i =1,2,…, p且p仅能取8,7,6。

问题4的优化目标有两个，即成本更少和效能率大于0.8的加工包最多。因此目标函数为双目标函数
$$s.t.\{\begin{array}{rl}minST& =\sum _{i=1}^p{S}_i\\ maxET& =\sum _{i=1}^{p}g(E{C}_i)\end{array}$$其中p可取6，7，8

先考虑加工成本的目标，根据题目要求，加工成本只考虑点火成本$S_i^1$和加工量成本$S_i^2$。

点火成本 $S_i^1\in 400,500,600$

加工窖的加工成本：
$$S_i=S_i^1+S_i^2\ast W{C}_i=S_i^1+S_i^2\ast \sum _{j=1}^{16}{w}_{ij}加工窖的加工成本：$$

总成本：
加工窖的加工成本：
$$ST=\sum _{i=1}^p{S}_i加工窖的加工成本：$$

对于双目标函数优化问题，进行线性加权转化为单目标优化问题，另外，需以对于两个单目标函数优化的最优值为基准建立新的目标函数进行优化。

用ST’表示加工成本的基准，ET’表示效能率大于0.8的加工包数量的基准，则
$$\{\begin{array}{rl}E{T}^{\prime }& =E{T}_{max}\\ S{T}^{\prime }& =S{T}_{min}\end{array}$$

综上我们建立的目标函数为：
加工窖的加工成本：
$$max0.5\ast \frac{S{T}^{\prime }}{minST}+0.5\ast \frac{maxET}{E{T}^{\prime }}加工窖的加工成本：$$

约束条件为：
$$s.t.\{\begin{array}{rl}{W}_i& =\sum _{j=1}^{16}{w}_{ij}\times E_j\\ W{C}_i& =\sum _{j=1}^{16}{w}_{ij}\\ P_{im}& \le W{C}_i\le P_{hm}\\ W{C}_i& \ge 500,n=1\\ W{C}_i& -w_{ij}>0,j=10,n\ge 2\\ K_i& =10,n=1\\ C_i& \in B\end{array}$$

目标函数的求解：

1.先只在搜索过程考虑单目标优化的情况，即成本较低的情况。分别求出单个加工窖的加工成本再进行累加，得到加工过程的总成本，求出总成本最低的最优解。

2.结合1的结果与第3问的结果，分别以这两个最优解为初始值再进行遍历搜索，从而得到同时满足两者的结果。

经过优化计算可得目标函数的最优解为0.9548，即线性加权后的目标函数最优解，对应的加工成本为14350元，效能率大于0.8的加工包数量为5个。图7为最优解所对应的原料配比。

问题五题解

分析

问题5的建模与求解过程是综合考虑前4个问题的求解结果进行优化计算的， 问题5共有3个目标函数，属于多目标函数优化问题。由于这3个目标函数的求解算法已经写好，因此我们直接采用前文的算法进行求解。假设饲料质量、加工成本和效能率对工厂加工的重要性相等，我们分别赋予每个指标 各三分之一的权系数，以问题2、问题3和问题4求解的最优值作为基准，建立新的目标函数进行优化。

求解

问题5要求给出混合加工方案使得饲料质量尽量高、加工成本尽量低、平均效能率超过80%的加工包尽量多。该问题综合问题2-4的三个优化目标，属于多目标函数优化问题。因此，可以采用线性加权法建立新的目标函数，在加权时，令饲料质量、加工成本、效能率大于0.8的加工包数量的权重相同，都为1/3，以问题2、问题3、问题4的求解结果为基准建立目标函数，进行优化。

令ST’、ET’、QT’分别表示只考虑总加工成本的最优解，只考虑效能率大于0.8加工包数量的最优解和饲料质量的最优解。故
$$\{\begin{array}{rl}E{T}^{\prime }& =E{T}_{max}\\ S{T}^{\prime }& =S{T}_{min}\\ Q{T}^{\prime }& =Q{T}_{max}\end{array}$$

按照问题5的要求，建立目标函数：
$$max\frac{1}{3}\ast \frac{S{T}^{\prime }}{minST}+\frac{1}{3}\ast \frac{maxET}{E{T}^{\prime }}+\frac{1}{3}\ast \frac{maxQT}{Q{T}^{\prime }}$$

该优化问题的求解过程与问题4类似，但以问题2、3、4中的最优值为基准进行搜索，用python编写程序求最优解。

求解结果：

经优化模型可得如图8 配比为最优解，线性加权后得目标函数得最优解为0.9091，在此种配比情况下平均亲缘值为4.660331，即为质量最好，成本为14474元，效能率大于0.8的加工包数量为4。

附录代码

工具函数

	def get_blood():
	a='a';b='b';c='c';d='d';e='e';f='f';g='g';h='h';
	i='i';j='j';k='k';l='l';m='m';n='n';o='o';p='p';
	q='q';r='r';s='s';t='t';u='u';v='v';w='w';x='x';
	y='y';z='z';
	
	breed=[[] for i in range(16)]
	breed[0]=[a,b,c,d,e,f,g,h,i,j]
	breed[1]=[a,b,c,d,e,o,p,k,l,m]
	breed[2]=[f,g,h,a,j,o,p,k,l,m]
	breed[3]=[f,g,h,i,j,l,p,f,o,p]
	breed[4]=[f,b,h	,d,	e	,o	,p,	a	,o	,z]
	breed[5]=[r,m,t	,u	,q,	f,	g	,a,	f	,z]
	breed[6]=[r,s,t	,u	,k	,f	,g	,h	,f,	c]
	breed[7]=[r,s,t	,u	,a	,b	,h	,i	,j	,c]
	breed[8]=[c,s,a	,f	,v	,w	,a	,i	,j	,c]
	breed[9]=[b,m,n	,i	,a	,z	,h	,f	,o	,z]
	breed[10]=[m,a,m,e	,a	,z	,a	,b	,a	,b]
	breed[11]=[m,c,m,e	,x	,h,	a	,b	,n	,a]
	breed[12]=[b,a,n,y	,c	,g	,m	,b	,m	,b]
	breed[13]=[m,c,m,y,	x,	g,	m,	b,	n,	b]
	breed[14]=[b,x,n,i,	c,	l,	b,	c,	m,	p]
	breed[15]=[c,c,a,f,	x,	h,	b,	c,	m,	j]
	
	blood=np.zeros([16,16])
	for i in range(16):
	for j in range(16):
	flag=0
	for k in range(10):
	if breed[i][k]==breed[j][k]:
	flag+=1
	blood[i][j]=flag
	
	#blood_pd = pd.DataFrame(blood)
	return blood
	
	'''计算加工后的一个加工包的质量'''
	def get_weight(target,breed):
	t=0
	for i in target:
	t=t+breed[i][0]*breed[i][1]
	return t
	
	'''计算加工前的一个加工包的质量'''
	def get_weight2(target,breed):
	t=0
	for i in target:
	t=t+breed[i][0]
	return t
	
	'''计算一个加工包的平均亲缘值'''
	def cal_blood(target,blood):
	t=0
	combine  = list(itertools.combinations(target, 2))   
	if len(combine)==0:
	return 10
	for i in combine: 
	t=t+blood[i[0]][i[1]]
	t=t/len(combine)
	return t    
	
	'''计算一个方案的平均亲缘值'''
	def get_quality(target,blood):
	blood1=[0 for i in range(9)]
	blood2=0
	for i in range(9):
	blood1[i]=blood1[i]+cal_blood(target[i],blood)
	blood2=blood2+get_weight(target[i],breed)*blood1[i]
	return blood2/4840
	
	'''方案描述方法转换'''
	def trans(a):
	pit=[[] for i in range(9)]
	for i in range(16):
	pit[a[i]-1].append(i)
	return pit
	
	'''求一个加工窖平均能耗率数'''
	def get_e_single(target):
	t1=0
	t2=0
	for i in target:
	t1=t1+breed[i][0]*breed[i][1]
	t2=t2+breed[i][0]
	if t2==0:
	return 0
	t1=t1/t2
	return t1
	
	
	'''求一个方案中平均能耗率大于0.8的个数'''
	def get_e(target):
	flag=0
	for i in target:
	if get_e_single(i)>0.8:
	flag+=1
	return flag
	
	'''求一个方案的成本'''
	def get_price(target):
	t=0
	for i in range(9):
	t=t+pit[i][2]+get_weight2(target[i],breed)*pit[i][3]   
	return t

Q1

import matplotlib.pyplot as plt
	import seaborn as sns
	import pandas as pd
	import numpy as np
	
	def get_blood():
	a='a';b='b';c='c';d='d';e='e';f='f';g='g';h='h';
	i='i';j='j';k='k';l='l';m='m';n='n';o='o';p='p';
	q='q';r='r';s='s';t='t';u='u';v='v';w='w';x='x';
	y='y';z='z';
	
	breed=[[] for i in range(16)]
	breed[0]=[a,b,c,d,e,f,g,h,i,j]
	breed[1]=[a,b,c,d,e,o,p,k,l,m]
	breed[2]=[f,g,h,a,j,o,p,k,l,m]
	breed[3]=[f,g,h,i,j,l,p,f,o,p]
	breed[4]=[f,b,h	,d,	e	,o	,p,	a	,o	,z]
	breed[5]=[r,m,t	,u	,q,	f,	g	,a,	f	,z]
	breed[6]=[r,s,t	,u	,k	,f	,g	,h	,f,	c]
	breed[7]=[r,s,t	,u	,a	,b	,h	,i	,j	,c]
	breed[8]=[c,s,a	,f	,v	,w	,a	,i	,j	,c]
	breed[9]=[b,m,n	,i	,a	,z	,h	,f	,o	,z]
	breed[10]=[m,a,m,e	,a	,z	,a	,b	,a	,b]
	breed[11]=[m,c,m,e	,x	,h,	a	,b	,n	,a]
	breed[12]=[b,a,n,y	,c	,g	,m	,b	,m	,b]
	breed[13]=[m,c,m,y,	x,	g,	m,	b,	n,	b]
	breed[14]=[b,x,n,i,	c,	l,	b,	c,	m,	p]
	breed[15]=[c,c,a,f,	x,	h,	b,	c,	m,	j]
	
	blood=np.zeros([16,16])
	for i in range(16):
	for j in range(16):
	flag=0
	for k in range(10):
	if breed[i][k]==breed[j][k]:
	flag+=1
	blood[i][j]=flag
	
	#blood_pd = pd.DataFrame(blood)
	return blood
	
	blood=get_blood()
	#sns.heatmap(blood, cmap='Reds')
	#plt.show()
	\end{
     lstlisting}

Q2

	
	blood=get_blood()
	pit=[[300,600,400,2],[300,600,400,2],[300,600,400,2],[600,900,500,1.8],[600,900,500,1.8],[600,900,500,1.8],
	[900,1200,600,1.6],[900,1200,600,1.6],[900,1200,600,1.6]]
	breed=[[300,0.88],[500,0.6],[200,0.93],[500,0.9],[300,0.9],[400,0.78],[300,0.7],[300,0.83],[400,0.95],
	[600,0.87],[100,0.65],[600,0.75],[500,0.8],[400,0.68],[300,0.87],[300,0.83]]
	
	breed_break=[[100,0.88],[100,0.88],[100,0.88],
	[100,0.6],[100,0.6],[100,0.6],[100,0.6],[100,0.6],
	[100,0.93],[100,0.93],
	[500,0.9],
	[300,0.9],
	[400,0.78],
	[300,0.7],
	[300,0.83],
	[400,0.95],
	[600,0.87],
	[100,0.65],
	[600,0.75],
	[500,0.8],
	[400,0.68],
	[300,0.87],
	[300,0.83]]
	
	count=0
	max_blood=0
	result=[]
	
	t_pit=[[] for i in range(9)]
	
	for i0 in range(9):
	if get_weight(t_pit[i0],breed)+breed[0][0]<=pit[i0][1]:
	t_pit[i0].append(0)
	else:
	continue
	for i1 in range(9):
	if get_weight(t_pit[i1],breed)+breed[1][0]<=pit[i1][1]:
	t_pit[i1].append(1)
	else:
	continue
	for i2 in range(9):
	if get_weight(t_pit[i2],breed)+breed[2][0]<=pit[i2][1]:
	t_pit[i2].append(2)
	else:
	continue
	for i3 in range(9):
	if get_weight(t_pit[i3],breed)+breed[3][0]<=pit[i3][1]:
	t_pit[i3].append(3)
	else:
	continue
	for i4 in range(9):
	if get_weight(t_pit[i4],breed)+breed[4][0]<=pit[i4][1]:
	t_pit[i4].append(4)
	else:
	continue
	for i5 in range(9):
	if get_weight(t_pit[i5],breed)+breed[5][0]<=pit[i5][1]:
	t_pit[i5].append(5)
	else:
	continue
	for i6 in range(9):
	if get_weight(t_pit[i6],breed)+breed[6][0]<=pit[i6][1]:
	t_pit[i6].append(6)
	else:
	continue
	for i7 in range(9):
	if get_weight(t_pit[i7],breed)+breed[7][0]<=pit[i7][1]:
	t_pit[i7].append(7)
	else:
	continue
	for i8 in range(9):
	if get_weight(t_pit[i8],breed)+breed[8][0]<=pit[i8][1]:
	t_pit[i8].append(8)
	else:
	continue
	for i9 in range(9):
	if get_weight(t_pit[i9],breed)+breed[9][0]<=pit[i9][1]:
	t_pit[i9].append(9)
	else:
	continue
	for i10 in range(9):
	if get_weight(t_pit[i10],breed)+breed[10][0]<=pit[i10][1]:
	t_pit[i10].append(10)
	else:
	continue
	for i11 in range(9):
	if get_weight(t_pit[i11],breed)+breed[11][0]<=pit[i11][1]:
	t_pit[i11].append(11)
	else:
	continue
	for i12 in range(9):
	if get_weight(t_pit[i12],breed)+breed[12][0]<=pit[i12][1]:
	t_pit[i12].append(12)
	else:
	continue
	for i13 in range(9):
	if get_weight(t_pit[i13],breed)+breed[13][0]<=pit[i13][1]:
	t_pit[i13].append(13)
	else:
	continue
	for i14 in range(9):
	if get_weight(t_pit[i14],breed)+breed[14][0]<=pit[i14][1]:
	t_pit[i14].append(14)
	else:
	continue
	for i15 in range(9):
	if get_weight(t_pit[i15],breed)+breed[15][0]<=pit[i15][1]:
	t_pit[i15].append(15)
	count+=1
	flag=0
	
	for constraint in range(9):
	if get_weight2(t_pit[constraint],breed)<pit[constraint][0] or t_pit[constraint]==[9] or (len(t_pit[constraint])==1 and breed[t_pit[constraint][0]][0]<500):                 
	flag=1
	break  
	
	
	if get_quality(t_pit,blood)>+max_blood and flag==0:                                                                       
	max_blood=get_quality(t_pit,blood)
	print(t_pit,max_blood)
	result=copy.copy(t_pit)                                                                   
	else:
	continue
	t_pit[i15].remove(15)
	t_pit[i14].remove(14)
	t_pit[i13].remove(13)
	t_pit[i12].remove(12)
	t_pit[i11].remove(11)
	t_pit[i10].remove(10)
	t_pit[i9].remove(9)
	t_pit[i8].remove(8)                                   
	t_pit[i7].remove(7)
	t_pit[i6].remove(6)
	t_pit[i5].remove(5)
	t_pit[i4].remove(4)
	t_pit[i3].remove(3)
	t_pit[i2].remove(2)
	t_pit[i1].remove(1)
	t_pit[i0].remove(0)
	
	#get_quality(trans(a),blood)
	\end{
     lstlisting}

Q3

	for i0 in range(9):
	if get_weight(t_pit[i0],breed)+breed[0][0]<=pit[i0][1]:
	t_pit[i0].append(0)
	else:
	continue
	for i1 in range(9):
	if get_weight(t_pit[i1],breed)+breed[1][0]<=pit[i1][1]:
	t_pit[i1].append(1)
	else:
	continue
	for i2 in range(9):
	if get_weight(t_pit[i2],breed)+breed[2][0]<=pit[i2][1]:
	t_pit[i2].append(2)
	else:
	continue
	for i3 in range(9):
	if get_weight(t_pit[i3],breed)+breed[3][0]<=pit[i3][1]:
	t_pit[i3].append(3)
	else:
	continue
	for i4 in range(9):
	if get_weight(t_pit[i4],breed)+breed[4][0]<=pit[i4][1]:
	t_pit[i4].append(4)
	else:
	continue
	for i5 in range(9):
	if get_weight(t_pit[i5],breed)+breed[5][0]<=pit[i5][1]:
	t_pit[i5].append(5)
	else:
	continue
	for i6 in range(9):
	if get_weight(t_pit[i6],breed)+breed[6][0]<=pit[i6][1]:
	t_pit[i6].append(6)
	else:
	continue
	for i7 in range(9):
	if get_weight(t_pit[i7],breed)+breed[7][0]<=pit[i7][1]:
	t_pit[i7].append(7)
	else:
	continue
	for i8 in range(9):
	if get_weight(t_pit[i8],breed)+breed[8][0]<=pit[i8][1]:
	t_pit[i8].append(8)
	else:
	continue
	for i9 in range(9):
	if get_weight(t_pit[i9],breed)+breed[9][0]<=pit[i9][1]:
	t_pit[i9].append(9)
	else:
	continue
	for i10 in range(9):
	if get_weight(t_pit[i10],breed)+breed[10][0]<=pit[i10][1]:
	t_pit[i10].append(10)
	else:
	continue
	for i11 in range(9):
	if get_weight(t_pit[i11],breed)+breed[11][0]<=pit[i11][1]:
	t_pit[i11].append(11)
	else:
	continue
	for i12 in range(9):
	if get_weight(t_pit[i12],breed)+breed[12][0]<=pit[i12][1]:
	t_pit[i12].append(12)
	else:
	continue
	for i13 in range(9):
	if get_weight(t_pit[i13],breed)+breed[13][0]<=pit[i13][1]:
	t_pit[i13].append(13)
	else:
	continue
	for i14 in range(9):
	if get_weight(t_pit[i14],breed)+breed[14][0]<=pit[i14][1]:
	t_pit[i14].append(14)
	else:
	continue
	for i15 in range(9):
	if get_weight(t_pit[i15],breed)+breed[15][0]<=pit[i15][1]:
	t_pit[i15].append(15)
	count+=1
	flag=0
	
	for constraint in range(9):
	if get_weight2(t_pit[constraint],breed)<pit[constraint][0] or t_pit[constraint]==[9] or (len(t_pit[constraint])==1 and breed[t_pit[constraint][0]][0]<500):                 
	flag=1
	break  
	
	
	if get_e(t_pit)>max_e and flag==0:                                                                       
	max_e=get_e(t_pit)
	print(t_pit,max_e)
	result=copy.copy(t_pit)                                                                   
	else:
	continue
	t_pit[i15].remove(15)
	t_pit[i14].remove(14)
	t_pit[i13].remove(13)
	t_pit[i12].remove(12)
	t_pit[i11].remove(11)
	t_pit[i10].remove(10)
	t_pit[i9].remove(9)
	t_pit[i8].remove(8)                                   
	t_pit[i7].remove(7)
	t_pit[i6].remove(6)
	t_pit[i5].remove(5)
	t_pit[i4].remove(4)
	t_pit[i3].remove(3)
	t_pit[i2].remove(2)
	t_pit[i1].remove(1)
	t_pit[i0].remove(0)
	\end{
     lstlisting}

Q4

	for i0 in range(9):
	if get_weight(t_pit[i0],breed)+breed[0][0]<=pit[i0][1]:
	t_pit[i0].append(0)
	else:
	continue
	for i1 in range(9):
	if get_weight(t_pit[i1],breed)+breed[1][0]<=pit[i1][1]:
	t_pit[i1].append(1)
	else:
	continue
	for i2 in range(9):
	if get_weight(t_pit[i2],breed)+breed[2][0]<=pit[i2][1]:
	t_pit[i2].append(2)
	else:
	continue
	for i3 in range(9):
	if get_weight(t_pit[i3],breed)+breed[3][0]<=pit[i3][1]:
	t_pit[i3].append(3)
	else:
	continue
	for i4 in range(9):
	if get_weight(t_pit[i4],breed)+breed[4][0]<=pit[i4][1]:
	t_pit[i4].append(4)
	else:
	continue
	for i5 in range(9):
	if get_weight(t_pit[i5],breed)+breed[5][0]<=pit[i5][1]:
	t_pit[i5].append(5)
	else:
	continue
	for i6 in range(9):
	if get_weight(t_pit[i6],breed)+breed[6][0]<=pit[i6][1]:
	t_pit[i6].append(6)
	else:
	continue
	for i7 in range(9):
	if get_weight(t_pit[i7],breed)+breed[7][0]<=pit[i7][1]:
	t_pit[i7].append(7)
	else:
	continue
	for i8 in range(9):
	if get_weight(t_pit[i8],breed)+breed[8][0]<=pit[i8][1]:
	t_pit[i8].append(8)
	else:
	continue
	for i9 in range(9):
	if get_weight(t_pit[i9],breed)+breed[9][0]<=pit[i9][1]:
	t_pit[i9].append(9)
	else:
	continue
	for i10 in range(9):
	if get_weight(t_pit[i10],breed)+breed[10][0]<=pit[i10][1]:
	t_pit[i10].append(10)
	else:
	continue
	for i11 in range(9):
	if get_weight(t_pit[i11],breed)+breed[11][0]<=pit[i11][1]:
	t_pit[i11].append(11)
	else:
	continue
	for i12 in range(9):
	if get_weight(t_pit[i12],breed)+breed[12][0]<=pit[i12][1]:
	t_pit[i12].append(12)
	else:
	continue
	for i13 in range(9):
	if get_weight(t_pit[i13],breed)+breed[13][0]<=pit[i13][1]:
	t_pit[i13].append(13)
	else:
	continue
	for i14 in range(9):
	if get_weight(t_pit[i14],breed)+breed[14][0]<=pit[i14][1]:
	t_pit[i14].append(14)
	else:
	continue
	for i15 in range(9):
	if get_weight(t_pit[i15],breed)+breed[15][0]<=pit[i15][1]:
	t_pit[i15].append(15)
	count+=1
	flag=0
	
	for constraint in range(9):
	if get_weight2(t_pit[constraint],breed)<pit[constraint][0] or t_pit[constraint]==[9] or (len(t_pit[constraint])==1 and breed[t_pit[constraint][0]][0]<500):                 
	flag=1
	break  
	
	
	if get_price(t_pit)>max_p and flag==0:                                                                       
	max_p=get_price(t_pit)
	print(t_pit,max_p)
	result=copy.copy(t_pit)                                                                   
	else:
	continue
	t_pit[i15].remove(15)
	t_pit[i14].remove(14)
	t_pit[i13].remove(13)
	t_pit[i12].remove(12)
	t_pit[i11].remove(11)
	t_pit[i10].remove(10)
	t_pit[i9].remove(9)
	t_pit[i8].remove(8)                                   
	t_pit[i7].remove(7)
	t_pit[i6].remove(6)
	t_pit[i5].remove(5)
	t_pit[i4].remove(4)
	t_pit[i3].remove(3)
	t_pit[i2].remove(2)
	t_pit[i1].remove(1)
	t_pit[i0].remove(0)