leetcode 593. Valid Square

Given the coordinates of four points in 2D space, return whether the four points could construct a square.

The coordinate (x,y) of a point is represented by an integer array with two integers.

Example:

Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,1]
Output: True

Note:

1. All the input integers are in the range [-10000, 10000].
2. A valid square has four equal sides with positive length and four equal angles (90-degree angles).
3. Input points have no order.

就是看4个点是否构成的是正方形。

package leetcode;

import java.util.Arrays;

public class Valid_Square_593 {

	public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
		int[] allBian=new int[]{
				getDistance2(p1, p2),getDistance2(p1, p3),getDistance2(p1, p4),
				getDistance2(p2, p3),getDistance2(p2, p4),getDistance2(p3, p4)
		};
		Arrays.sort(allBian);
		if(allBian[0]==0){
			return false;
		}
		//保证有4个边相同,a^2可能比a大，也可能比a小
		if(allBian[0]==allBian[3]||allBian[2]==allBian[5]){
			//a^2比a大
			if(allBian[0]==allBian[3]){
				//使用勾股定理:a^2+b^2=c^2，而a=b，所以2a^2=c^2
				if(allBian[0]*2==allBian[5]){
					return true;
				}
			}
			else{//a^2比a小
				if(allBian[5]*2==allBian[0]){
					return true;
				}
			}
		}
		return false;
	}
	
	//返回距离的平方
	int getDistance2(int[] p1,int[] p2){
		int distance2=(p1[0]-p2[0])*(p1[0]-p2[0])+(p1[1]-p2[1])*(p1[1]-p2[1]);
		return distance2;
	}

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Valid_Square_593 v = new Valid_Square_593();
		int[] p1 = new int[] { 0, 0 };
		int[] p2 = new int[] { 0, 0 };
		int[] p3 = new int[] { 0, 0 };
		int[] p4 = new int[] { 0, 0 };
		System.out.println(v.validSquare(p1, p2, p3, p4));
	}

}

我为什么算距离的平方，而不是直接算距离呢？因为一个根号下去，变成double类型，有可能出现精度问题。如根号2=1.4142135623731...，但是1.4142135623731的平方=2.000000004，不等于2。

大神说：如果4点连成的是正方形，那么这4个点之间的6条线，一定有4条相等，另外2条也相等，且4条的长度不等于2条的长度。4条是边，2条是斜边。

public class Solution {
    public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
        HashMap map = new HashMap<>();
        int a12 = getDistanceSquare(p1, p2);
        int a13 = getDistanceSquare(p1, p3);
        int a14 = getDistanceSquare(p1, p4);
        int a23 = getDistanceSquare(p2, p3);
        int a24 = getDistanceSquare(p2, p4);
        int a34 = getDistanceSquare(p3, p4);
        if (a12 == 0 || a13 == 0 || a14 == 0 || a23 == 0 || a24 == 0 || a34 == 0){
                return false;
        }
        map.put(a12, map.getOrDefault(a12, 0) + 1);
        map.put(a13, map.getOrDefault(a13, 0) + 1);
        map.put(a14, map.getOrDefault(a14, 0) + 1);
        map.put(a23, map.getOrDefault(a23, 0) + 1);
        map.put(a24, map.getOrDefault(a24, 0) + 1);
        map.put(a34, map.getOrDefault(a34, 0) + 1);
        return map.size() == 2 && (map.get(a12) == 2 || map.get(a12) == 4);

    }
    
    private int getDistanceSquare(int[] a, int[] b) {
        return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]);
    }
}

这道题有solutions： https://leetcode.com/problems/valid-square/solution/。

Solution

---

Approach #2 Using Sorting [Accepted]

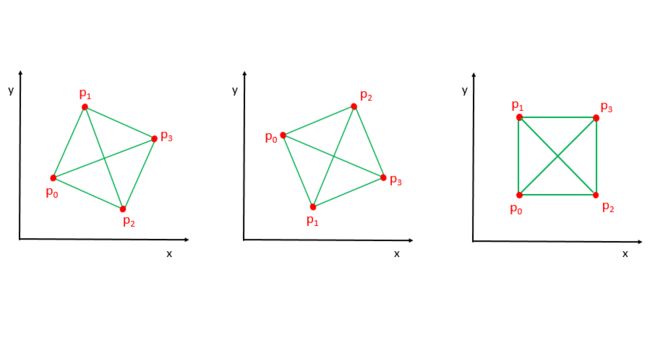
我们可以不考虑边的所有可能组合情形，而是根据x坐标大小，来对这4个坐标进行排序。如果4个点能构成正方形，且四个坐标按照x坐标从小到大排序为p0,p1,p2,p3，那么构成的正方形只可能是下面3种情况：

这三种情况下，四条边和斜边都是如下的结论:

1. p_0p_1p​0​​p​1​​, p_1p_3p​1​​p​3​​, p_3p_2p​3​​p​2​​ and p_2p_0p​2​​p​0​​ form the four sides of any valid square.

2. p_0p_3p​0​​p​3​​ and p_1p_2p​1​​p​2​​ form the diagonals of the square.

因此，我们可以比较 p_0p_1p​0​​p​1​​, p_1p_3p​1​​p​3​​, p_3p_2p​3​​p​2​​ and p_2p_0p​2​​p​0​​ 的长度，和 p_0p_3p​0​​p​3​​ and p_1p_2p​1​​p​2​​ 的长度。（注意，菱形的话两条斜边是不相等的。）

Java

public class Solution {
    public double dist(int[] p1, int[] p2) {
        return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]);
    }
    public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
        int[][] p={p1,p2,p3,p4};
        Arrays.sort(p, (l1, l2) -> l2[0] == l1[0] ? l1[1] - l2[1] : l1[0] - l2[0]);
        return dist(p[0], p[1]) != 0 && dist(p[0], p[1]) == dist(p[1], p[3]) && dist(p[1], p[3]) == dist(p[3], p[2]) && dist(p[3], p[2]) == dist(p[2], p[0])   && dist(p[0],p[3])==dist(p[1],p[2]);
    }
}

Complexity Analysis

• Time complexity : $O(1)$. Sorting 4 points takes constant time.

• Space complexity : $O(1)$. Constant space is required.

---

Approach #3 Checking every case [Accepted]

Algorithm

我们考虑所有组合的可能性（点 按照顺时针排序）：

在图中，相同背景色代表“边集合和斜边集合”相同的情况。我们发现只有3种与众不同的情形。因此，没必要考虑24种情况，只需要看这3种情况。

Java

public class Solution {
    public double dist(int[] p1, int[] p2) {
        return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]);
    }
    public boolean check(int[] p1, int[] p2, int[] p3, int[] p4) {
        return dist(p1,p2) > 0 && dist(p1, p2) == dist(p2, p3) && dist(p2, p3) == dist(p3, p4) && dist(p3, p4) == dist(p4, p1) && dist(p1, p3) == dist(p2, p4);
    }
    public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
        return check(p1, p2, p3, p4) || check(p1, p3, p2, p4) || check(p1, p2, p4, p3);
    }
}

Complexity Analysis

• Time complexity : $O(1)$. A fixed number of comparisons are done.

• Space complexity : $O(1)$. No extra space required.