图论的基础 小白笔录
图论
注释:本文只是提供各个知识点的基础知识,模板类知识。
图的遍历与连通性+图的存储(邻接矩阵)
洛谷 图的遍历

很基础的一个遍历,不过好像不能用正序找最大值,会爆内存,要用倒序,比如点1到点4,那么我们从4遍历,只要与4联通的都是4最大
拓扑排序
最大食物链计数
dfs,这题是求从最弱动物到最强动物的路劲数,而不是深度。
所以可以bfs,dfs求
我这里用dfs
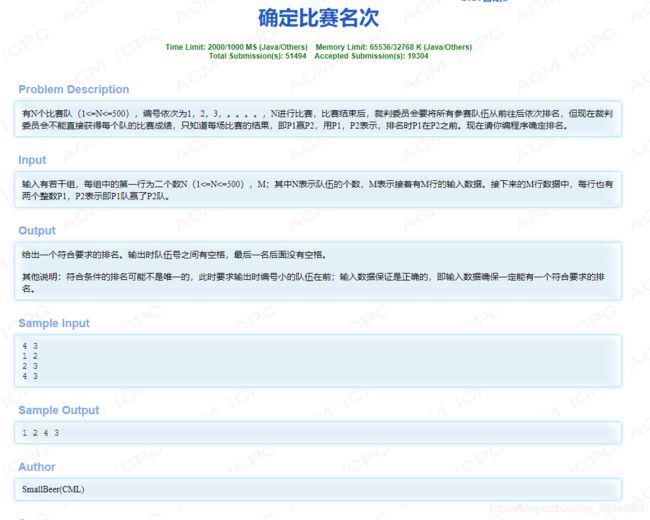
hdu1285 确定比赛名次
bfs+优先队列
这个方法不需要判重,只要注意输出格式就行,为何不用判重,给一组数据为 1 2,2 3,2 3,4 3,其中2到3式重边,但是不碍事,虽然这代码中visit[3]=3,但是edge[2]=[3,3],在bfs判断now=2结点时,会进行2次删减,所以就等于一个。

力扣207 课程表
这题要判断有没有环,判断环的方法很简单,bfs时不断进入queue,在q为空的时候会退出循环,如果这时候我们访问的点的数量小于存在的点的数量,那么就是环。因为环当中的点,不会入队列。


力扣210 课程表II

和上一题几乎一样,就在q队列里删除操作后,加入ans数组,bfs返回bool来判断有没有环,有环返回空,无环返回ans
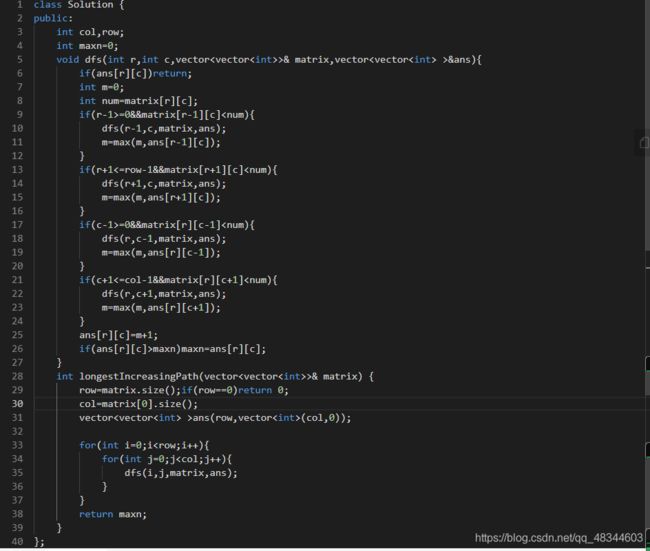
力扣329 矩阵中的最长递增路径
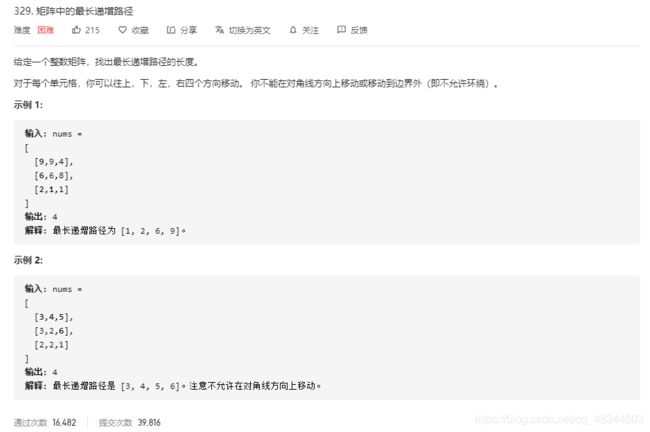
经典记忆化dfs题,我也不知道为何和拓扑排序搞在了一起。。。
当然,确实可以拓扑排序,先把整个地图的低洼处找出来,即入度为0,对周围的点的入度减一,如果入度为0,进队列,计数器++,因为最长路径肯定在低洼处,所以遍历所有的低洼处,bfs把最长路径得到,最后比较就行。
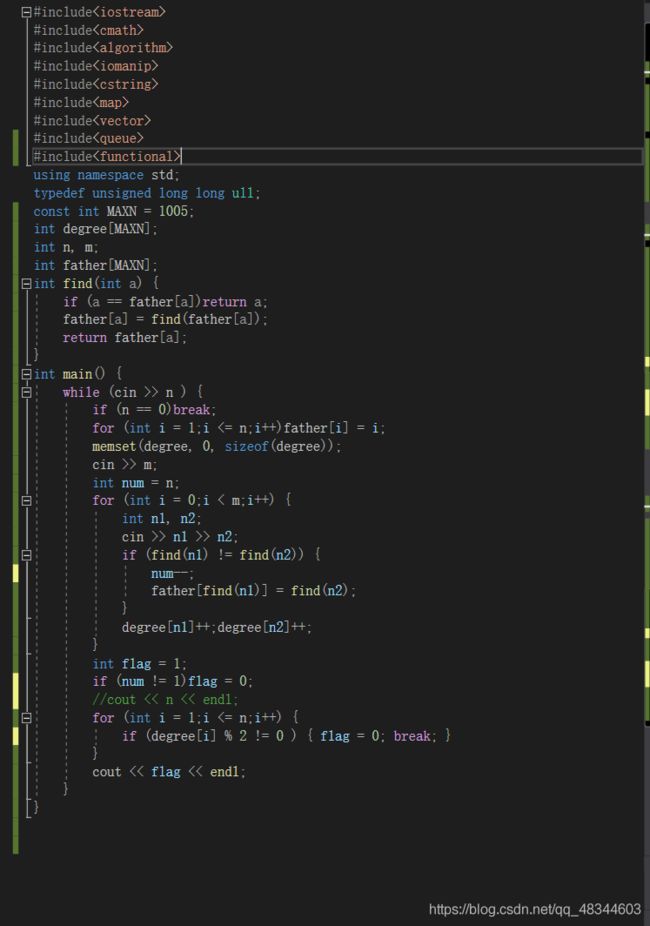
欧拉回路
判断一个无向图是不是欧拉回路,每个点的度数(出度加入度)为偶数(不能为0,不然点独立成图),并且要保证时一个图,即可以一笔画成。
保证是不是一个图,用并查集。
对于每个点的度数,则只要开个degree数组记录就行。
hdu1978 欧拉回路
hdu1116 Play on Words
上面一题是无向图的欧拉回路
这题是判断有向图的欧拉通路
有向图的欧拉通路是所有点度数为0,则是欧拉回路,如果有2个点度数一个为-1,一个为1,那么是通路。这里我们对每个单词的首尾2个字母进行联通。


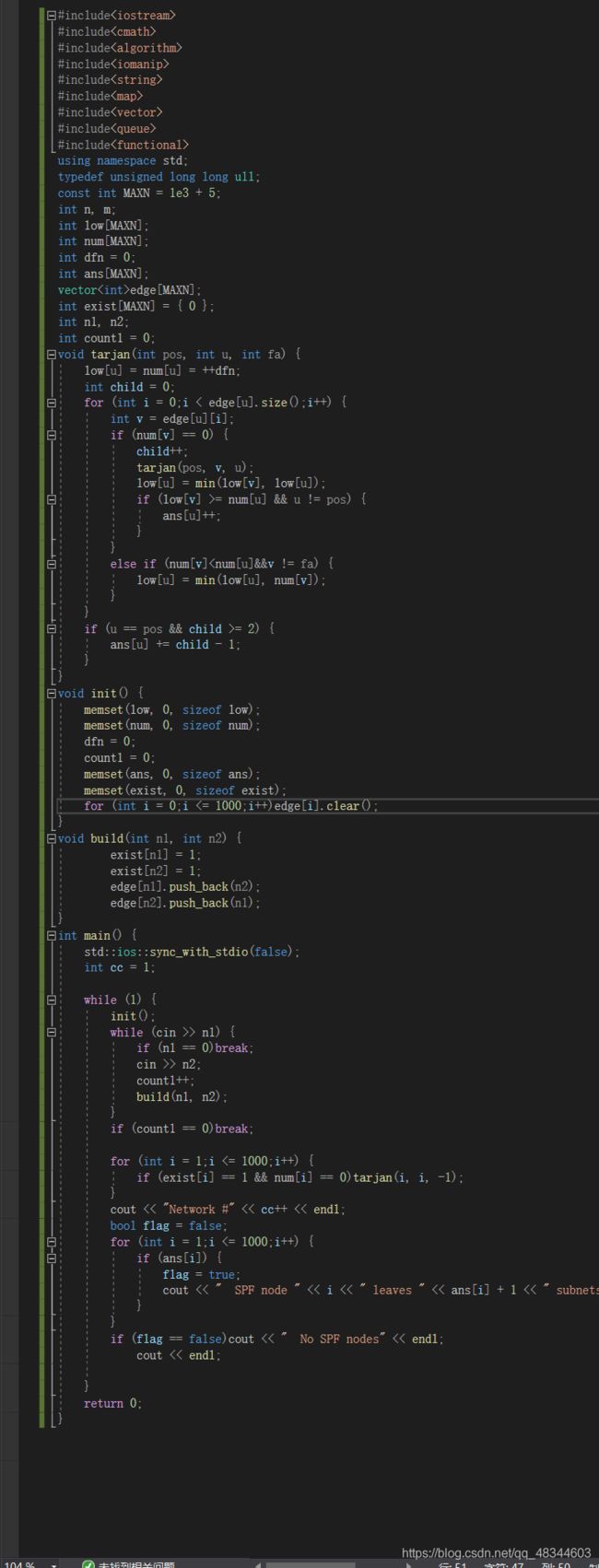
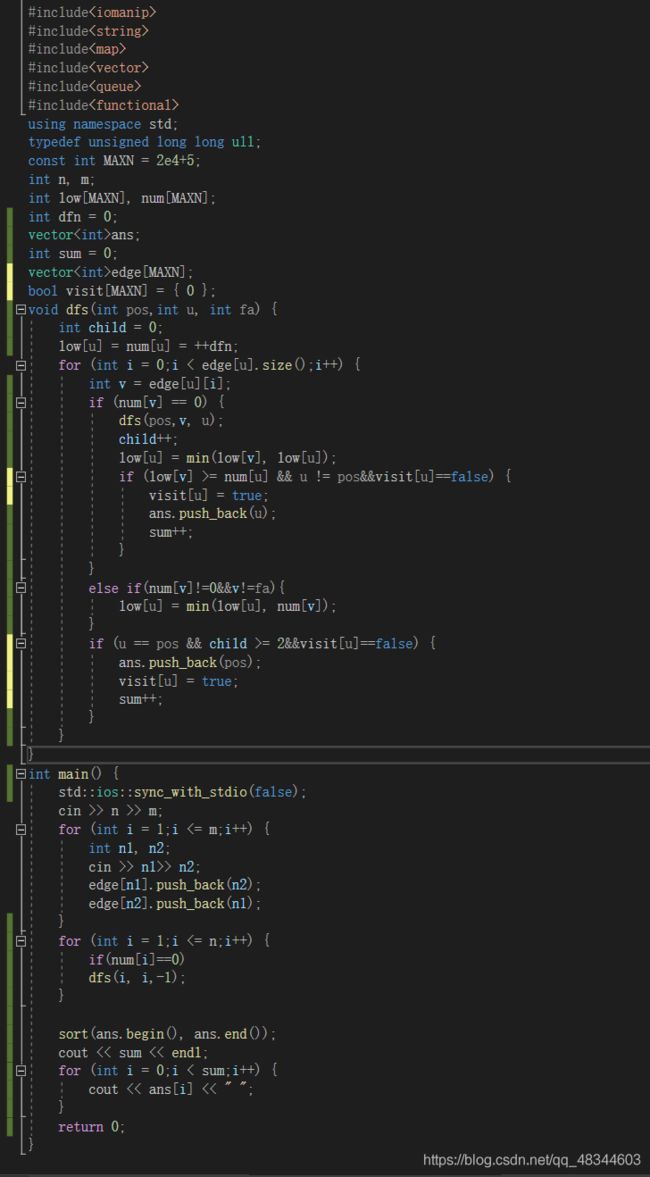
割点割边
洛谷P3380 割点
概念应该都了解,基础代码原理自己也应该要去查博客什么的自己弄清楚,我这边就讲一下一些比较细的地方:
pos是祖先结点,因为图不一定连通,所有祖先不止一个。
1、用dfn表示时间戳,记录递归的顺序(不是递归的深度,是顺序,表示这个点在什么时候才被递归到)
2、child++放在if(num[v]==0)里的原因,给你两组数据比较就知道了:① 3 3,1 2,1 3,2 3②3 2,1 2,1 3————》第一个child是1,第二个child值是2
3、为何要用visit标记这个是不是割点:如果为false,表示这个割点没被访问过,我们放进去,如果为true,表示访问过了,如果不加这判断,同样的割点我们要放进去很多次,当然,你也可以用set存储割点,然后再排序。
4、dfs里,为何else if里要判断v!=fa,fa是u的父亲,v是u的孩子,我们对一个点判断是否访问过了,父亲肯定是被访问过的,因为这个结点就是从父亲结点递归下来的,所以这个不断回退边
5、割边的判断条件从if(low[v]>=num[u]&&u!=pos)更改为if(low[v]>num[u]&&u!=pos),读者自己想一下,割点表示孩子v最多回到u,所以u是割点,而第二个条件表示孩子不走父亲结点那条路最多能回到自身。u->v这是割边。

双连通分量
边 poj3352 Road Construction
这里用到了缩点的技术,缩点是什么意思呢,就是把一个环变成一个点,把环里的一个值或者一个情况用一个点表示。这里就把low值相同的作为环,然后让记录环的度数(此时环被看成是个点)
不妨想一下,环的度数为1,是不是就表示这个环与外面的环就只有一边连接着,为2就是2条边等等,这题给我们一个无向图,问我们加多少边可以让图变为双连通图。就是让环所有的度数都不为1,这题保证了图是连通的,如果图不连通,那么我们dfs要枚举点,并且用一个visit记录我们是否访问过这个点,我们一个dfs就可以把一个图给遍历完,所有属于这个图的visit值都会为true,为false的我们会继续遍历,然后各做各的统计结果。

点 poj1523 SPF
模板点连通分量,但是刚理解还是不明白,其实这题就是求割点,访问到了割点u,用个ans[u]记录几次访问到了这割点,除了根节点,其他结点被分成的点连通分量==割点的访问次数+1,根节点要特判。你也许不理解,自己画个图。证明呢,我讲简单点,就是一个割点(注意是割点,去掉的话,图就分开了)至少连接着2个图吧,好,那么要访问到这个割点(除了根节点,所以根节点特判)肯定要通过一个图访问到这个割点,那么通过这个图访问这个割点,导致这个割点的父节点是这个图,就比如SPF第一张图,访问3,,肯定要从点1,2,3这张图访问过来,所以,由于1或2是他父节点,父节点又不参与计算他的子节点的割点数,导致点连通分量少了1。根节点就要特判,因为是直接访问的,没有父节点,所以所有的割点访问数就是连通分量数。(我代码为了答案最后都输出+1,所以让根节点的减一)
这里点不连续,所以用exist记录到底有没有这个点,count1来记录到底输入什么时候结束。ans[]来记录答案。
有向图的连通性(Tarjan算法)
hdu1269 迷宫城堡
个人认为和割边很相似,都是分low值,low值相同则是一个强连通。

为何用scc记录,因为scc记录后表示这个值在一个强连通里,dfs已经经过了,那个if如果不判的话,一个点会等于另一个强连通图的low值,会出错。
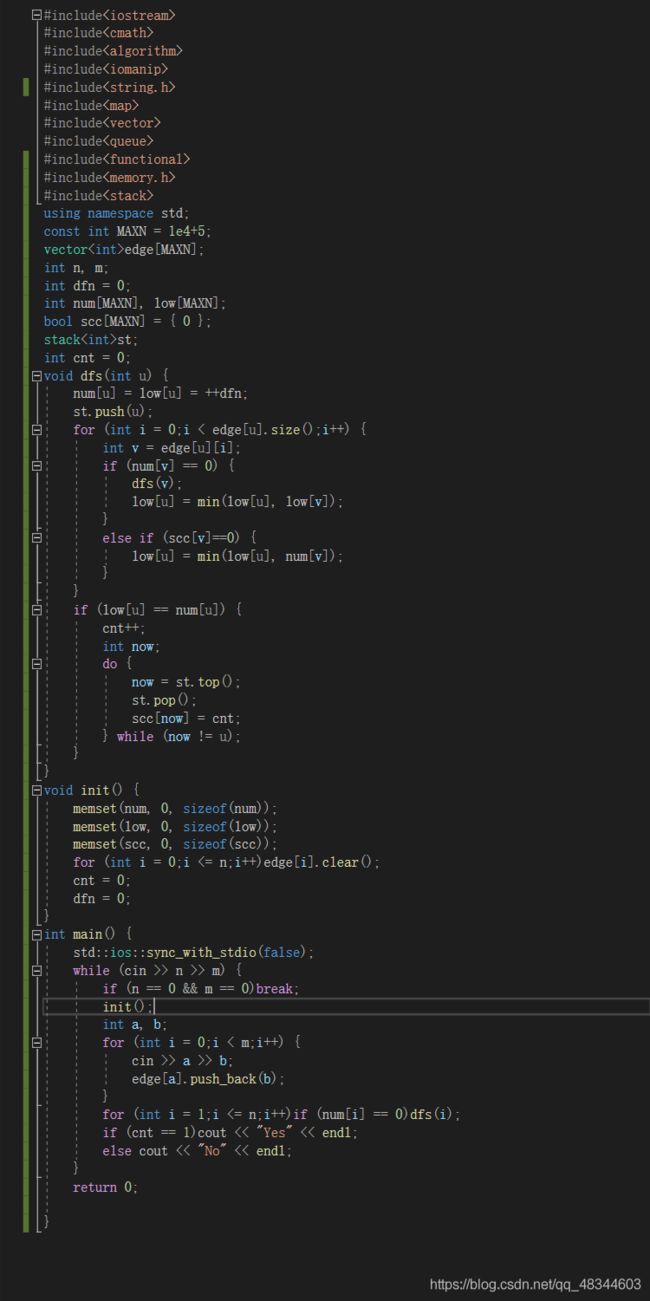
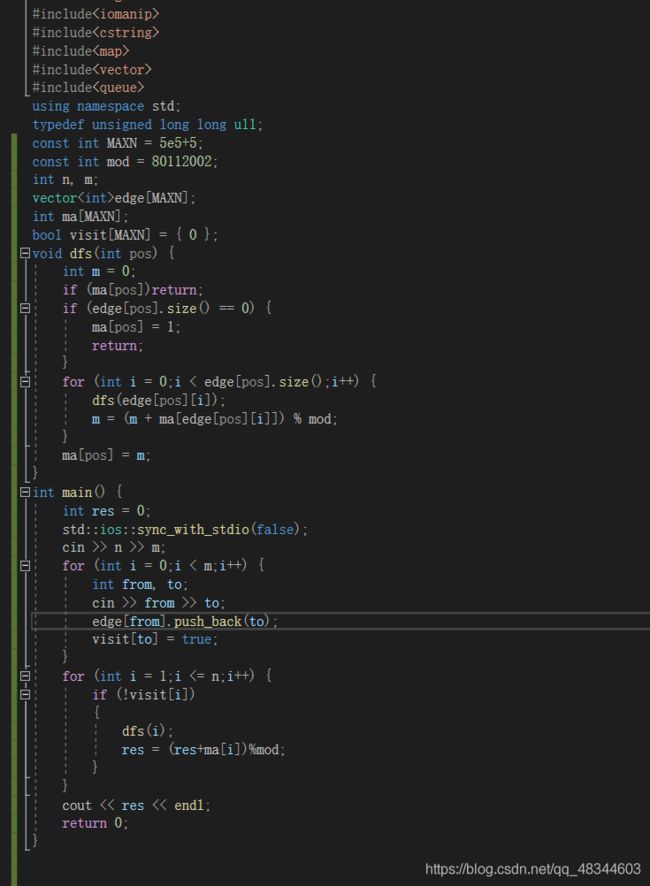
hdu1827 Summer Holiday
有向连通+缩点+小小的拓扑

首先进行tarjan将所有的点能缩的缩一下,其次,对于缩点后的点,遍历得到入度,入度为0的,则是需要加入的,入读不为0呢?自然是由入读为0的打电话。

最短路
hdu2544 最短路(SPFA解法)
SPFA是一个可以判断负权的图问题,我这里用邻接表来进行操作,数据大的话用链式前向星。
SPFA用队列来存储更新值,什么是更新值,就是我们在遍历一个点的邻居时,要判断这个邻居到起点的最短距离,如果最短距离更新,就为更新值,一旦这点的最短距离更新,那么他的邻居的最短距离可能也要更新,所以将这个点入队列,等待更新他的邻居。
如何判断负值呢,我们就用一个数组来记录每个点入队列的次数,因为是负值,那么肯定会不断的进入队列。这样一旦这个次数超过点的数量,那么就是负值。为何是超过点的数量呢,因为一个图无负权的图,对于一个点的遍历次数肯定不会超过点数,哪怕每个点遍历后都要更新这个点,那么这个点也就遍历了n次,不会超过n次,所以我们用次数来记录是否由负值。

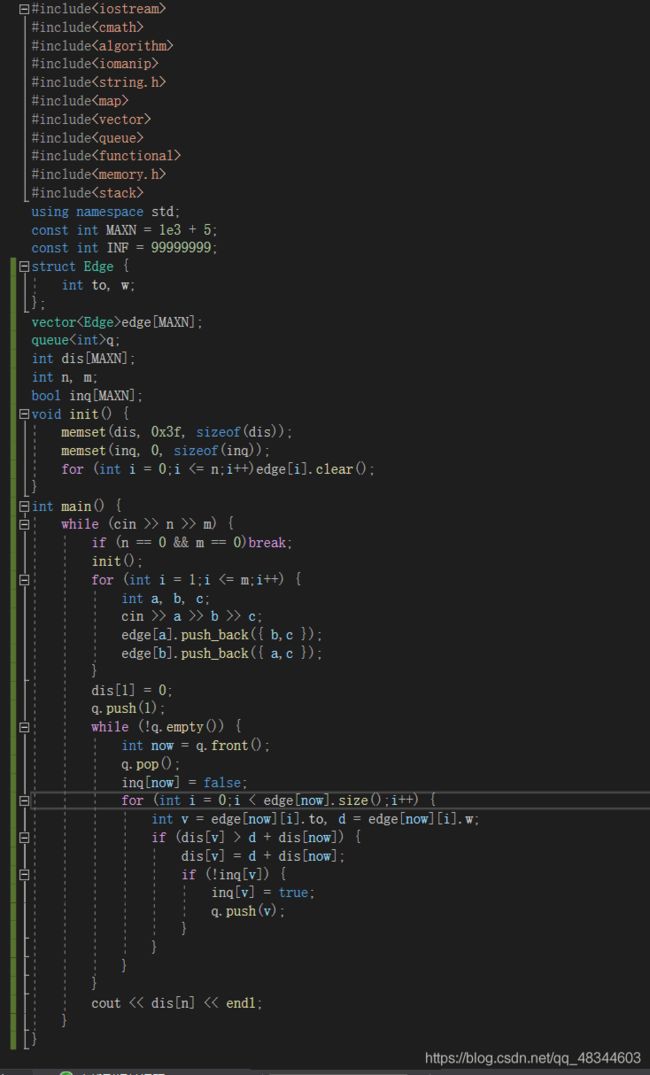
hdu2544 最短路(Dijkstra解法)
Dijkstra算法,厉害在所有点遍历一次便可,利用贪心思想,假如a点最近,那么所有未被访问过的点中,离a点最近的距离也是最近的,那么怎么弄未被访问过的点,我用isfind数组记录。第一次理解可能比较难,但是慢慢来,练习几次就明白了。
最小生成树
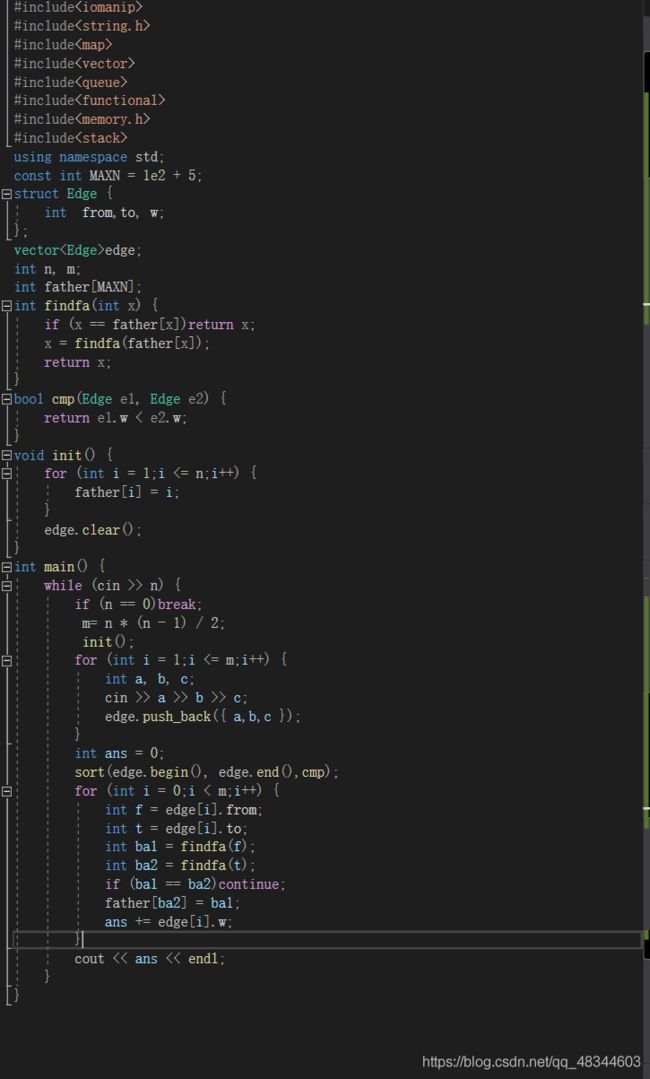
hdu1233 还是畅通工程
让图连通的最小代价,有按点结算,按边结算,这里是用边结算,代码简单。kruskal算法。
加上并查集。
先存边,后面对边进行排序。让边权值小的在前面,然后遍历边,找到最小边,如果这个边的from和to结点的祖先节点不同,那么加入答案。为何要要祖先结点不同呢,不妨想一下,我们在遍历这条边的时候,如果祖先结点相同,那么说明这2个点已经互相达到过了,而且是通过其他边绕路达到的,如果这时候我们再加上一天不绕路的边,那么2个点之间可以互相达到的路不止一条,会形成环,就不是最小生成树了。
最大生成树
hdu5627 Clarke and MST
最大生成树和最小生成树差不多,都是连通一次,但是最大生成树要求是权值和最大。

最大流
初次学习,这涉及到比较多的从没听过的词语。建议b站找老师教学。
https://www.bilibili.com/video/BV1Q7411R7ie?from=search&seid=1722308642042257985
这把最大流基础讲清楚了,我听了一遍也就了解了。很入门的讲解。
我认为EK算法虽然暴力,但是算是入门了。思想和Ford-Fulkerson方法一样。不断构建残留网络,在残留网络中找出路,如果找不到了,就是已经找完了,只要把每次找到的残留网络中的flow值加起来便可,为何bfs呢,因为dfs的话在一些数据上迭代次数太多。pre数组记录每次bfs的路径,为了在EK中能够对根据路径进行构建残留网络。
hdu1523 Drainage Ditches(EK算法)
洛谷P3376 【模板】最大流(Dinic算法)
这题我学了dinic来做,对新手来说,dinic看上去难,其实思路还是很简单的,先bfs更新每个点的层数,然后dfs遍历求值。那会不会遗漏不是最近的层的解呢,答案是不会,因为我们main函数里bfs在while里,只要true,不断bfs,而bfs一次,就会dfs很多次,并且把相应的残留网络遍历,而我们再次遍历时,那么有些层数的边的权值已经更新为0,不能再计算了。
其次为何dis初始化为INF,而不是-1那种,因为如果是-1,在起始点的时候dis是0,如果一旦起始点有环,那么会进入循环,超时。
这里用链式前向星,而不是vector数组存图,是因为vector存图反向边难找,当然也可以二维数组存图。
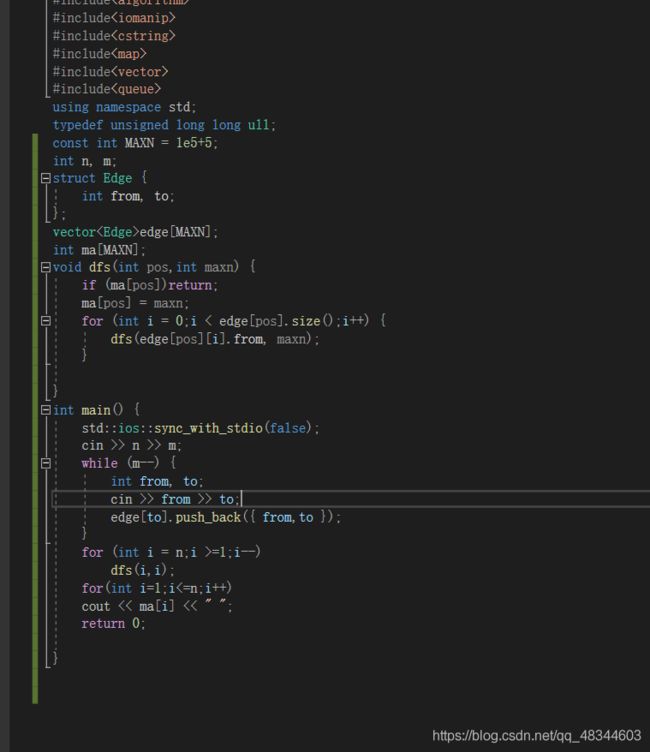
hdu1956 Sightseeing tour
有向图与无向图的欧拉回路判断,首先我们有向图和无向图的判断方式都知道,无向图是点都是偶数点,则是欧拉回路,有向图是,所有点度数为0。对于混合图,我们把无向边转化为有向边。
这里肯定要和度数存在关系。我们对于有向边的2个点的出度入度是可以计算的,但是无向边就不行,所以,我们着重判断无向边,我们先随意将无向边的方向定义一个方向,得到所有点的出度与入度,然后,入读减出度得到度数,度数大于0表示入度大,小于0则出度大,等于0表示正好,我们不动。然后我们要知道一旦一个点的度数为奇数,不管怎么处理边的方向,都会得到度数-2或度数+2,还是奇数,不可能是0。所以只处理偶数度,我们令s为所有 度数小于0的源点,t为所有度数大于0的汇点,s->i的流量为degree/2,因为这样一旦可以满流时,也就表示,举个例子,对于出度为4的,我们s到它的流量为2,这样满流时,我们可以把有流的边反过来,正好和无流的边的度数和为0,同理,其他边也是,那中间度数为0的点会不会改变度数呢,不会,假如,我们一个点入度2,出度为2的点,其中一条边为有向边,我们代码里等于将有向边忽略不看,对于3条无向边,我们会经过,也会形成残留地图,但是最后的结点度数和肯定是0,一出一进,抵消。

最小割
常见的最小割都是最大流枚举。复杂度V^3*E,比较大。怎么是最小割呢,就是对于一个图,我们让它断流,最小要堵住多少的路径。暴力法就是枚举所有点,把所有点当作是汇点。得到如果最大流最小,那么就是把这个点的入边割点就是最小的。
最小费用最大流
poj2135 Farm Tour

这题我用邻接表存储,没用链式前向星,主要为了搭配spfa。最小费用最大流题目就是在最大流的前提下,求得最小费用。我们先遍历一边得到一个最小费用,计算它的费用,然后构建残留网络,在残留网络中继续找最小费用。这里是无向图,所以我们要建立正反2边,并且每一边都有一个残留边,费用为-c,因为如果你反悔不走这条边,那么你的费用就要减去。这里的路径长度相当于费用,我们令其他的流量限制为1,构建起始点s和t,并且流量设置为2,费用为0,为何呢,流量2保证我们往返各一次,费用为0保证不影响结果。
建立边用了pre表示是反向边的位置。这个比链式前向星麻烦,链式的只要i^1就行,而这个要记录。后面的pre数组和prei数组都是记录前驱点的位置。这题用链式前向星会简单点,不过spfa会麻烦。

二分图匹配
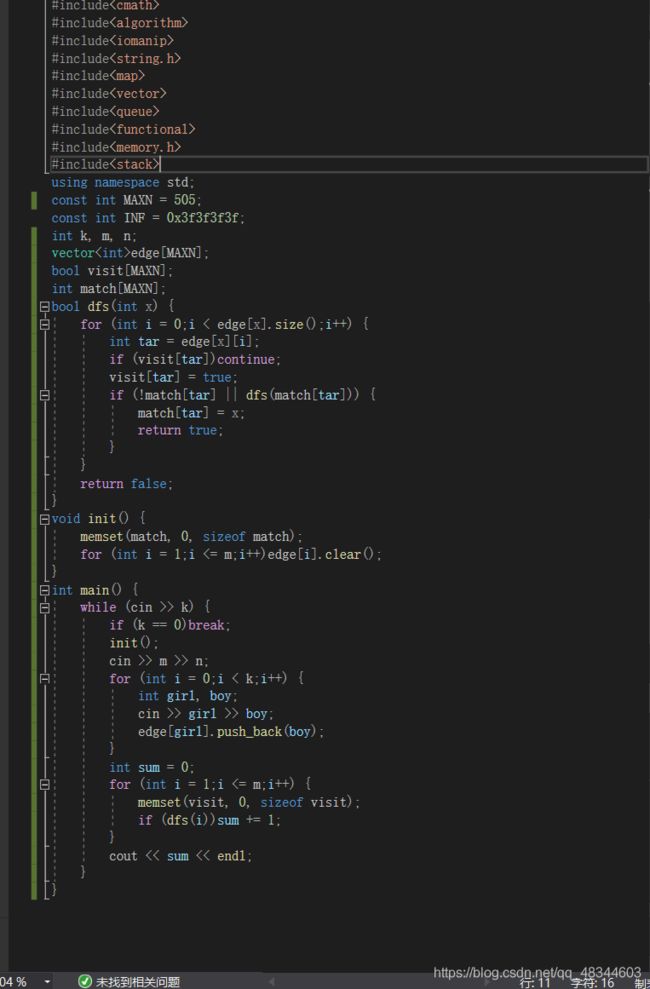
hdu2063 过山车

二分图就是简单的最大流问题,如果看成最大流的话,那么就是定义一个超级源点和超级汇点,把女生和源点连起来,男生和汇点连起来,然后每个边的流量都是1,保证配对。
这个是匈牙利算法,假如一个女的配对成功,后面女的还要配对这个男的,那么我们就让前面的女的换一个对象,如果换不了返回false,否则返回true。