【LeetCode】498. 对角线遍历 & 1424. 对角线遍历 II

I、498. 对角线遍历（蛇形）

一、题目描述

给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

示例:

输入:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]

输出:  [1,2,4,7,5,3,6,8,9]

解释:

说明:

给定矩阵中的元素总数不会超过 100000 。

二、解题思路 & 代码

2.1 对角线迭代和翻转

算法

1. 初始化数组 result，用于存储最后结果。
2. 使用一个外层循环遍历所有的对角线。第一行和最后一列的元素都是对角线的起点。
3. 使用一个内层 while 循环遍历对角线上的所有元素。可以计算指定对角线上的元素数量，也可以简单迭代直到索引超出范围。
4. 因为不知道每条对角线上的元素数量，需要为每条对角线分配一个列表或动态数组。但是同样也可以通过计算得到当前对角线上的元素数量。
5. 对于奇数编号的对角线，只需要将迭代结果翻转再加入结果数组即可。

class Solution:
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:

        if not matrix or not matrix[0]:
            return []

        N, M = len(matrix), len(matrix[0])
        
        result, intermediate = [], []
        
        for d in range(N + M - 1):
            # Clear the intermediate array everytime we start
            # to process another diagonal
            intermediate.clear()
            
            # We need to figure out the "head" of this diagonal
            # The elements in the first row and the last column
            # are the respective heads.
            r, c = 0 if d < M else d - M + 1, d if d < M else M - 1
            
            # Iterate until one of the indices goes out of scope
            # Take note of the index math to go down the diagonal
            while r < N and c > -1:
                intermediate.append(matrix[r][c])
                r += 1
                c -= 1
            
            # Reverse even numbered diagonals. The
            # article says we have to reverse odd 
            # numbered articles but here, the numbering
            # is starting from 0 :P
            if d % 2 == 0:
                result.extend(intermediate[::-1])
            else:
                result.extend(intermediate)
        return result        

复杂度分析

• 时间复杂度：$O(N\cdot M)$，数组有 N 行 M 列。对于所有奇数对角线上的元素，需要两次处理，迭代和翻转。为了节省空间，需要遍历新对角线之前清除中间使用的空间，该操作需要$O(K)$ 的复杂度度，其中 K 是数组长度。因此至少处理两次数组中的元素，渐进复杂度为 $O(N\cdot M)$。
• 空间复杂度：$O(min(N,M))$，额外空间用于存储每条对角线的中间数组，该数组长度为 N 和 M 的最小值。注意：对角线延伸到索引超出范围结束。

2.2 模拟

算法

1. 初始化一个布尔变量 direction 表示当前对角线的方向。根据当前方向和尾部位置确定下一条对角线首部。最初 direction 为 1，方向向上。每条对角线遍历完成后更新 direction。
2. 假设当前对角线首部为 $matrix[i][j]$，根据方向遍历该对角线。
   1）向上的对角线，下一个元素是 $matrix[i-1][j+1]$。
   2）向下的对角线，下一个元素是 $matrix[i+1][j-1]$。
3. 遍历当前对角线元素直到到达矩阵边界结束。
4. 假设现在到达当前对角线的最后一个元素，寻找下一条对角线首部。注意：下面伪代码中方向是当前对角线方向。如果当前对角线方向是向上的，则下一条对角线是向下的；否则是下一条对角线是向上的。

tail = [i, j]
if direction == up, then {
   if [i, j + 1] is within bounds, then {
       next_head = [i, j + 1]
   } else { 
       next_head = [i + 1, j]
   }
} else {
   if [i + 1, j] is within bounds, then {
       next_head = [i + 1, j]
   } else { 
       next_head = [i, j + 1]
   }
}

5. 继续处理对角线元素，当前对角线遍历结束时，使用当前方向和尾部位置找出下一条对角线首部。然后翻转方向，处理下一条对角线。

class Solution:
    
    def findDiagonalOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix or not matrix[0]:
            return []
        
        N, M = len(matrix), len(matrix[0])
        row, column = 0, 0
        direction = 1
        result = []
        
        while row < N and column < M:
            
            result.append(matrix[row][column])
            
            # Move along in the current diagonal depending upon
            # the current direction.[i, j] -> [i - 1, j + 1] if 
            # going up and [i, j] -> [i + 1][j - 1] if going down.
            new_row = row + (-1 if direction == 1 else 1)
            new_column = column + (1 if direction == 1 else -1)
            
            # Checking if the next element in the diagonal is within the
            # bounds of the matrix or not. If it's not within the bounds,
            # we have to find the next head. 
            if new_row < 0 or new_row == N or new_column < 0 or new_column == M:
                
                # If the current diagonal was going in the upwards
                # direction.
                if direction:
                    
                    # For an upwards going diagonal having [i, j] as its tail
                    # If [i, j + 1] is within bounds, then it becomes
                    # the next head. Otherwise, the element directly below
                    # i.e. the element [i + 1, j] becomes the next head
                    row += (column == M - 1)
                    column += (column < M - 1)
                else:
                    
                    # For a downwards going diagonal having [i, j] as its tail
                    # if [i + 1, j] is within bounds, then it becomes
                    # the next head. Otherwise, the element directly below
                    # i.e. the element [i, j + 1] becomes the next head
                    column += (row == N - 1)
                    row += (row < N - 1)
                    
                # Flip the direction
                direction = 1 - direction        
            else:
                row = new_row
                column = new_column
                        
        return result                 

复杂度分析

• 时间复杂度：$O(N\cdot M)$，每个元素只处理一次。
• 空间复杂度：$O(1)$，不使用额外空间。注意：输出数组空间不计入空间复杂度，因为这是题目要求的空间。空间复杂度应该指除了最终数组以外的空间。上一个方法中是中间数组，该方法中只有几个变量。

参考：

1. LeetCode官方题解

===============================================================================================================================

II、1424. 对角线遍历 II（同向）

给你一个列表 nums ，里面每一个元素都是一个整数列表。请你依照下面各图的规则，按顺序返回 nums 中对角线上的整数。

示例 1：

输入：nums = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,4,2,7,5,3,8,6,9]

示例 2：

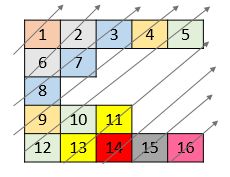
输入：nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
输出：[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

示例 3：

输入：nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
输出：[1,4,2,5,3,8,6,9,7,10,11]

示例 4：

输入：nums = [[1,2,3,4,5,6]]
输出：[1,2,3,4,5,6]

提示：

1 <= nums.length <= 10^5
1 <= nums[i].length <= 10^5
1 <= nums[i][j] <= 10^9
nums 中最多有 10^5 个数字。

二、解题思路 & 代码

$nums[i][j]$ 必然在第（i + j）次斜线的结果中。i 越小，结果越靠后。

class Solution:
    def findDiagonalOrder(self, nums: List[List[int]]) -> List[int]:
        sub_result = []
        for i in range(len(nums)):
            for j in range(len(nums[i])):
                if i + j >= len(sub_result):
                    sub_result.append([])
                sub_result[i + j].append(nums[i][j])
                
        result = []
        for sub in sub_result:
            result += sub[::-1]
        return result