leetcode1568. 使陆地分离的最少天数(Python3、c++)
文章目录
- leetcode1568. 使陆地分离的最少天数
-
- 方法:并查集
-
- 思路:
-
- 并查集:
- 求割点:
- 代码:
-
- Python3:
- cpp:
- 结果:
leetcode1568. 使陆地分离的最少天数
给你一个由若干 0 和 1 组成的二维网格 grid ,其中 0 表示水,而 1 表示陆地。岛屿由水平方向或竖直方向上相邻的 1 (陆地)连接形成。
如果 恰好只有一座岛屿 ,则认为陆地是 连通的 ;否则,陆地就是 分离的 。
一天内,可以将任何单个陆地单元(1)更改为水单元(0)。
返回使陆地分离的最少天数。
示例 1:
输入:grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
输出:2
解释:至少需要 2 天才能得到分离的陆地。
将陆地 grid[1][1] 和 grid[0][2] 更改为水,得到两个分离的岛屿。
示例 2:
输入:grid = [[1,1]]
输出:2
解释:如果网格中都是水,也认为是分离的 ([[1,1]] -> [[0,0]]),0 岛屿。
示例 3:
输入:grid = [[1,0,1,0]]
输出:0
示例 4:
输入:grid = [[1,1,0,1,1],
[1,1,1,1,1],
[1,1,0,1,1],
[1,1,0,1,1]]
输出:1
示例 5:
输入:grid = [[1,1,0,1,1],
[1,1,1,1,1],
[1,1,0,1,1],
[1,1,1,1,1]]
输出:2
提示:
1 <= grid.length, grid[i].length <= 30grid[i][j]为0或1
方法:并查集
思路:
首先需要仔细阅读这道题,问的是,经过几次操作,可以得到分离的陆地,即连通分量数大于等于2。那么**如果原来的连通分量数大于等于2或为0(全是水也可以看做陆地分离),那么不需要操作即为所求,直接返回0;**如果原来有一个连通分量,那么则需要考虑如何才能分成两个。
因为是网格图,我们可以知道,如果存在一个连通分量,那么这个连通分量一定存在一个角,比如连通分量四个角上的某个点,如下图所示。
对于这种角,每个角只与两个1相连,只要把这两个1变成0,那么就将这个角与原来图形的剩余部分分离了,也就完成陆地分离操作,由于所有图形都存在这种角,因此答案最大为2。
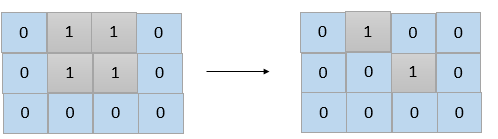
对于一些连通图形,我们只需要将一个点变为0即可完成分离,如下图所示:
我们只需将蓝色的1变为0即可为完成分割,这种点,我们称之为割点,如果存在割点,那么我们只需要1次操作就可以完成。找到割点的算法是Tarjan算法。由于Tarjan算法较为复杂,我还没有理解,因此,我们使用复杂度较高的,直接遍历每个1,将其改为0,再次调用并查集,看是否会使得连通分量数从1变为2,如果可以,说明存在割点,直接返回1。
总结下来,我们这题的解法应该是这样的:
- 首先判断初始情况下有多少个连通分量,如果0或大于等于2,直接返回0。(这一步可以通过dfs或并查集来完成)
- 对于只有一个连通分量的情况,我们遍历所有的1,将每个改为0,调用并查集看连通分量是否变为2,即是否存在割点,如果找到了,那么返回1,如果没找到,返回2。
并查集:
下面我们回顾一下用并查集来求连通分量个数的方法,直接看修改过的并查集的模板:
class UnionFind:
#初始化,一共n个节点的并查集
def __init__(self,n,m):
self.parent = [k for k in range(n)]
# num表示连通分量的个数,初始为m,m为n个点中,为1的个数。
self.num = m
#查找某个元素的根节点
def find(self,index):
if self.parent[index] == index:
return index
#递归进行路径压缩
self.parent[index] = self.find(self.parent[index])
return self.parent[index]
#合并两个下标对应的“森林”,合并之后num--
def union(self,index1,index2):
if self.find(index1) == self.find(index2):
pass
else:
self.num -= 1
self.parent[self.find(index2)] = self.find(index1)
我们使用下面的做法,首先遍历一次网格,找到1的数量m,初始化并查集。然后再次遍历网格,对于表格值为1的点,遍历它的上下左右四个点,如果相邻点也为1,则进行union操作,该操作会将两个点在并查集中合并,同时连通分量num–。
这个操作不需要考虑重复情况,比如a点遇到相邻b进行合并,遍历到b时,相邻点有a又进行合并,这种情况下,ab已经合并过,num就不会再更改了。
最后的num即为连通分量个数。
求割点:
如果此时num=1,我们再次遍历网格图,对每个1,将其改为0,再次计算连通分量个数,如果变为2,则说明存在割点,返回1,遍历结束如果不存在变为2的情况,那么就不存在割点,返回2。
如果上面计算后,连通分量变为0,那么也返回1(即原来只有一个1,且将该1变为0)。
这部分遍历的时间复杂度为O(n ^ 2),每改变一个1之后,计算连通分量的时间复杂度也为O(n ^ 2),因此总的时间复杂度为O(n ^ 4),若使用Tarjan算法,时间复杂度可以优化到O(n ^ 2)。
代码:
Python3:
class UnionFind:
#初始化,一共n个节点的并查集
def __init__(self,n,m):
self.parent = [k for k in range(n)]
# num表示连通分量的个数,初始为m,m为n个点中,为1的个数。
self.num = m
#查找某个元素的根节点
def find(self,index):
if self.parent[index] == index:
return index
#递归进行路径压缩
self.parent[index] = self.find(self.parent[index])
return self.parent[index]
#合并两个下标对应的“森林”,合并之后num--
def union(self,index1,index2):
if self.find(index1) == self.find(index2):
pass
else:
self.num -= 1
self.parent[self.find(index2)] = self.find(index1)
class Solution:
def minDays(self, grid: List[List[int]]) -> int:
n = len(grid)
m = len(grid[0])
# 第一次判断,如果连通分量数量不是1,直接返回0,不需要改变
if self.count(grid) != 1:
return 0
else:
# 如果是1,那么开始遍历每个1
for i in range(n):
for j in range(m):
if grid[i][j]:
# 将这个1改为0,再进行count计算连通分量,如果不是1了(可能是0或2)
# 则这个点是割点,返回1
grid[i][j] = 0
if self.count(grid) != 1:
return 1
# 否则将该点还原为1,继续遍历
grid[i][j] = 1
# 所有的点都不是割点,则返回2
return 2
# 通过并查集来计算连通分量个数
def count(self,grid):
n = len(grid)
m = len(grid[0])
ones = 0
# 首先找到1的个数,这个数量为初始的连通分量数
for i in range(n):
for j in range(m):
if grid[i][j]:
ones += 1
# 初始化并查集
uf = UnionFind(n*m,ones)
directions = [(-1,0),(1,0),(0,-1),(0,1)]
# 遍历每个点,如果该点为1且相邻点为1,进行合并操作
for i in range(n):
for j in range(m):
if grid[i][j]:
for xx,yy in directions:
x = i + xx
y = j + yy
if 0<=x<n and 0<=y<m and grid[x][y] == 1:
uf.union(i*m+j,x*m+y)
# 最后返回连通分量个数。
return uf.num
cpp:
class UnionFind {
public:
vector<int> parent;
// num表示连通分量的个数
int num;
UnionFind(int n,int m) {
// 集合的代表元素 parent 数组
parent.resize(n);
// 初始时每个集合的代表元素就是自身
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
num = m;
}
/* 查找 x 所在集合的代表元素,即父节点 */
int Find(int x) {
if (x != parent[x]) {
// 非集合代表元素,在递归调用返回的时候,将沿途经过的结点指向根节点
parent[x] = Find(parent[x]);
}
return parent[x];
}
/* 合并 x y 所在集合 */
void Union(int x, int y) {
// 先查找 x y 所在集合的代表元素
int px = Find(x), py = Find(y);
if (px != py) {
// 不在同一个集合,将 x 所在集合合并到 y 所在集合
parent[px] = py;
num --;
}
}
};
class Solution {
public:
int dx[4] = {
-1,0,1,0}, dy[4] = {
0,-1,0,1};
int minDays(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
if (count(grid) != 1) return 0;
else{
for (int i = 0; i < n; i ++)
for (int j = 0; j < m; j++)
if (grid[i][j] == 1){
grid[i][j] = 0;
if (count(grid)!=1) return 1;
grid[i][j] = 1;
}
return 2;
}
}
int count(vector<vector<int>>& grid){
int n = grid.size(), m = grid[0].size(),ones = 0;
for (int i = 0; i < n; i ++)
for (int j = 0; j < m; j++)
if (grid[i][j]) ones++;
UnionFind uf(n*m,ones);
for (int i = 0; i < n; i ++)
for (int j = 0; j < m; j++)
if (grid[i][j])
for (int k = 0; k < 4; k ++){
int x = i + dx[k],y = j + dy[k];
if (x >= 0 && x < n && y >= 0 && y < m && grid[x][y]){
uf.Union(i*m+j,x*m+y);
}
}
return uf.num;
}
};