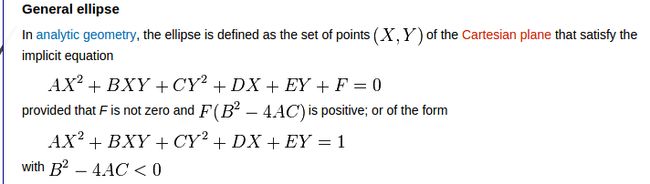opencv轮廓检测之椭圆检测-----算法篇(8) Hough transformation检测椭圆
其实如果应付的话, 我前面这篇文章 椭圆检测http://blog.csdn.net/traumland/article/details/51018133
对于场景已知, 精度不太要求, 效果还算不错(我之前在纸上画圆, 挖洞, 拿了带洞的的东西试过, 不过只是用椭圆去拟合, 没有办法分辨是不是椭圆)
因为有 拟合椭圆这个算法, 而且用了限制长短轴这种限定.
但是以后肯定有需要自己造轮子的时候, 没有准备到时候碰到不就眼蓝了么~~
椭圆需要的参数: 中心坐标(x,y), 旋转角, 长短半轴长 一共五个参数
像之前用霍夫变换的方法, 光是三维的parameter space 计算量就已经够大的了
而这里要创建五维的accumulator来存放parameter
要怎么简化?
http://www2.dis.ulpgc.es/~lalvarez/research/calibracion_elipse.pdf
上面这篇文章是讲圆形阵列标定的, 讲的也很详细,能用于标定那说明精度很好, 速度也不差, 会很有借鉴意义
如图, edge上的两个点切线相交(已知梯度), 得新交点(Xr, Yr), 然后讲交点与原二点构成弦的中点相连接,
圆心就在交点与中点的连线上. 所以再在edge上找另一个点与原两点之一进行同样的步骤, 即可找到中心坐标
上面这篇论文找到椭圆中心后, 用了最小二乘法来拟合椭圆
这里再提找中心的另一种方法, 就是通过一对梯度反向平行的两个点,
椭圆的中心坐标一定在它们之间的连线的中点处.
然而这种方法对于矩形等封闭对称的图形也适用, 并不针对椭圆, 所以需要进一步的约束条件来进行约束
确定好椭圆中心坐标后
接着确定其他三个参数
对于椭圆一般方程
图片来源http://math.wikia.com/wiki/Ellipse
因为A不等于0,
所以一般方程可以写成
![]()
已知(Xc, Yc), 有
这样就将五维的参数空间转化到三维
根据当求出来 B, C , F 时, 可求得长短半轴长与旋转角度
或者将上面式子进行求导, 得
然后这样就转化成二维, 求出B, C 再去反代入 上面那个式子, 求得F
read.pudn.com/downloads154/doc/682235/一种新的基于随机Hough变换的椭圆检测方法.pdf
------------------------------------------------------------------------------------------------------------------
我不知道是我关键字没选好, 还是百度学术不好用, 找出来的文章很少
所以也就放上这两篇文章吧
这两天 没办法google, 以后有钱就自己买吧
-------------------------------------------------------------------------------------------------------------------
试着写了一下程序, 憋了一整天.. 手推了一遍式子, 明天接着写
这两天稍微有点跑偏, 虽说数学和算法比较重要.. 可不是写一两个程序就能提高的
还是得动手写写看, 光用眼睛去看, 心理也会畏难不敢做.
---------------------------------------4.10 23:20
-------------------------------------------------------------------------------------------------------------------
写了提取椭圆中心的部分, 后面还没决定是用三维的参数矩阵, 还是用简化后的
感觉有点跑偏, 还是先找工作比较重要
先上代码吧, 我的github: 传送门
---------------------------------------4.11 20:30
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------
现在来看这段代码没有什么参考意义, 可以参考opencv霍夫变换源码的写法去写, 之前忘了像参数取值
范围、分辨率之类的东西应该是使用者自己输入的, 而且当时写的时候不知道多维参数空间怎么定义,
二维参数空间居然用了Mat来定义....
--------------------------------------6. 9 11:45