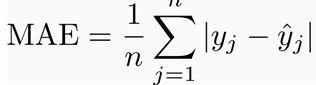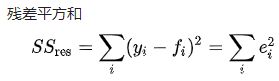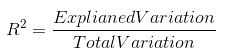如何评价回归算法的优劣 MSE、RMSE、MAE、R-Squared
如何评价回归算法的优劣 MSE、RMSE、MAE、R-Squared
- 前言
- 均方误差 MSE（Mean Squared Error）
-
- 代码实现
- 均方根误差（RMSE）
-
- 代码实现
- 平均绝对误差 （MAE）
- R Squared
-
- 代码实现
- 通过scikit-learn来计算metrics
- Notice
- MAE vs RMSE
前言
回归算法同分类算法不同，回归算法主要用来预测，而分类算法的目的是为了分类，所以两种算法的评判标准当然也不一样。
本文就是从MSE、RMSE、MAE、R-Squared四个指标来谈一谈如何衡量回归算法的好坏。
均方误差 MSE（Mean Squared Error）
均方误差是误差的平方的期望值，而误差是指估计值和被估计值的差。公式如下：
那么多少MSE才是最好的呢？理论上来说MSE=0是最好的，但是一般不可能达到，所以MSE越接近0越好。
但是这又面临另外一个问题，如果MSE越小，这就代表着模型更有可能Overfit（反之就是Underfit）。我们通常都是想要一个balance between overfit and underfit.
为了更详细的解释一下MSE，我们来手工计算一次：
有一列数组： (43,41),(44,45),(45,49),(46,47),(47,44)
- 通过这一些列数组得到回归方程如下：
- 将X带入方程获得相对应的 Y’ 预测值，如下：
9.2 + 0.8(43) = 43.6
9.2 + 0.8(44) = 44.4
9.2 + 0.8(45) = 45.2
9.2 + 0.8(46) = 46
9.2 + 0.8(47) = 46.8
- 预测值 Y’ 和实际值Y的差
41 – 43.6 = -2.6
45 – 44.4 = 0.6
49 – 45.2 = 3.8
47 – 46 = 1
44 – 46.8 = -2.8
- 将误差平方
目前值如下：
- 计算期望
将所有平方差加起来除以数量
（6.76 + 0.36 + 14.44 + 1 + 7.84）/ 5 =6.08
代码实现
y_predict=reg.predict(x_test) # reg是预测模型
mse=np.sum((y_predict-y_test)**2)/len(y_test)
均方根误差（RMSE）
RMSE（Root Mean Squard Error）均方根误差, 公式如下：
他是预测误差的标准偏差（standard deviation of residuals (predicted error)), 误差表示了实际点和预测回归线的距离，均方根误差表示这些点在回归线周围是怎么分布的。
也可以看作是平方根后的MSE
代码实现
rmse=mse**0.5
平均绝对误差 （MAE）
从公式可以看出来，预测值和实际值之差的绝对值除以n.
mae=np.sum(np.absolute(y_predict-y_test))/len(y_test)
R Squared
R-Squared 又叫做决定系数（coefficient of determination）
这个指标与其他不同的在于，R-squared消除了量纲上的影响，通过看这个数字来判断该模型有多fit？
Why？我们来通过公式来解释
总平方和：
yi是观测值，fi是预测值
当R越大越接近100%，说明更fit，反之则不fit
代码实现
r_squared=1-(np.sum((y_predict-y_test)**2)/np.var(y_test))
通过scikit-learn来计算metrics
from sklearn.metrics import mean_squared_error #均方误差
from sklearn.metrics import mean_absolute_error #平方绝对误差
from sklearn.metrics import r2_score#R square
#调用
mean_squared_error(y_test,y_predict)
mean_absolute_error(y_test,y_predict)
r2_score(y_test,y_predict)
Notice
以上三个Metrics不能单独令出一个来衡量模型，因为当一个metric看着很漂亮的时候很容易显示过拟合的状态，那么哪个更好呢？没有觉对的答案。
MAE vs RMSE
RMSE很容易受到极端值的影响，如下个例子：
假设你想了解量女朋友在准时方面的特点，你统计了近两个月女朋友约会的迟到时间（即是实际到达时间和约定时间的差距，或误差，单位可以是分钟，时间有夸大，我们只想你更好理解概念），如下：
第一个月迟到时间1 = ([5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 1000])
第二个月迟到时间2= ([5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10, 5, 10])
我们计算得出:
对于第一个月：平均绝对误差MAE2=62.5分钟,均方根误差RMSE2：235.82分钟
对于第二个月：平均绝对误差MAE1=7.5分钟,均方根误差RMSE1=7.91分钟
第一个月的平均绝对误差MAE(62.5)与均方根误差RMSE(235.82)之比接近1:4，第二个月迟到时间的平均绝对误差MAE(7.5)与均方根误差RMSE(7.91)之比约为1:1。我们应该用哪个量衡量女朋友守时呢？我们看到均方根误差RMSE受异常值的影响更大。如果我们去评判女朋友守时方面的进步，用RMSE标准，我们更可以看到她的进步之大，也许更要奖励她一顿饕餮盛宴。
一般来说，我们应该期望MAE值比RMSE值小得多。因为对于均方根误差RMSE,每个误差都是平方的。这意味着单个误差呈二次增长，并且对最终RMSE值有不同的影响。
这两组误差序列之间的惟一区别是序列1中的极值是1000，而不是10。因此，我们看到较大的异常值对均方根误差RMSE的影响更大。