空间相关分析(二) 全局莫兰指数的理解与计算
在了解空间权重矩阵的相关知识后,再展开对空间相关分析的学习就会变得轻松许多。而在空间相关分析中,全局相关分析和局部相关分析是比较常用的两个方法。今天,就来分享一下全局相关分析的有关知识。
目录
-
-
- 一、公式说明
- 二、深入理解
- 三、Moran'I指数检验
- 四、R和Geoda计算莫兰指数
-
- (1)R
- (2)Geoda
-
一、公式说明
在全局相关分析中,最常用的统计量就是Global Moran’I(全局莫兰指数),它主要是用来描述所有的空间单元在整个区域上与周边地区的平均关联程度。计算公式如下:
I = n S 0 × ∑ i = 1 n ∑ j = 1 n w i j ( y i − y ˉ ) ( y j − y ˉ ) ∑ i = 1 n ( y i − y ˉ ) 2 \mathit{I}=\frac{n}{S_{0}} \times \frac{\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}{w_{ij}(\mathit{y_{i}}-\bar{\mathit{y}})(\mathit{y_{j}}-\bar{\mathit{y}})}}{\sum\limits_{i=1}^{n}(\mathit{y_{i}}-\bar{\mathit{y}})^{2}} I=S0n×i=1∑n(yi−yˉ)2i=1∑nj=1∑nwij(yi−yˉ)(yj−yˉ)
其中, S 0 = ∑ i = 1 n ∑ j = 1 n w i j S_{0}=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}w_{ij} S0=i=1∑nj=1∑nwij, n \mathit{n} n为空间单元总个数, y i \mathit{y_{i}} yi和 y j \mathit{y_{j}} yj分别表示第 i \mathit{i} i个空间单元和第 j \mathit{j} j个空间单元的属性值, y ˉ \bar{y} yˉ为所有空间单元属性值的均值, w i j w_{ij} wij为空间权重值。
特别说明:这里的属性值取决你研究的对象。比如,若研究的是一个班上各个学生的成绩在空间上有无相关关系,则属性值就是学生成绩;若研究的是各个地区经济发展水平在空间有无相关关系,则属性值大多采用人均GDP来反映地区经济发展。
此外, I I I的取值范围为[-1,1],具体范围所代表含义如下表所示:
| I I I的范围 | 含义 |
|---|---|
| I > 0 I>0 I>0 | 表示所有地区的属性值在空间上有正相关性,即属性值越大(小)越容易聚集在一起 |
| I = 0 I=0 I=0 | 表示地区随机分布,无空间相关性 |
| I < 0 I<0 I<0 | 表示所有地区的属性值在空间上有负相关性,即属性值越大(小)越不容易聚集在一起 |
对于莫兰指数的取值范围为什么在这个区间,emm,我查阅了很多文献,里面也没有提到。这里仅谈下我自己的理解:因为这个公式与概率论中学习到的相关系数计算公式十分接近的,皮尔逊相关系数计算的公式如下,大家可以对比一下:
r = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 \mathit{r}=\frac{\sum\limits_{i=1}^{n}(\mathit{x_{i}-\bar{x}})(\mathit{y_{i}}-\bar{y})}{\sqrt{\sum\limits_{i=1}^{n}(\mathit{x_{i}-\bar{x}})^{2}\sum\limits_{i=1}^{n}(\mathit{y_{i}-\bar{y}})^{2}}} r=i=1∑n(xi−xˉ)2i=1∑n(yi−yˉ)2i=1∑n(xi−xˉ)(yi−yˉ)
由于莫兰指数是基于空间数据的计算,相当于是二维数据。单从分子来看,它仅比相关系数多了一个求和号以及空间权重,即将其拓展为空间上的相关系数。因此可以尝试从证明相关系数取值范围的方法去证明莫兰指数的取值范围(数学功底不错的小伙伴可以试着用柯西施瓦兹不等式试试)
emm,虽然balabala解释一大堆,但毕竟公式还是比较生涩难懂的。以下就以一个具体的例子来说明公式的含义。
以重庆市江津区、巴南区、南川区、綦江区为例,具体邻接情况如下图所示:
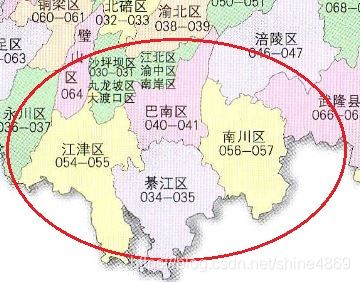
根据邻接情况,我们可以列个表
| 区名 | 相邻区名 |
|---|---|
| 江津区 | 巴南区、綦江区 |
| 巴南区 | 江津区、綦江区、南川区 |
| 南川区 | 巴南区、綦江区 |
| 綦江区 | 江津区、巴南区、南川区 |
根据上表,得出该四个区的一阶相邻空间权重矩阵 W W W为
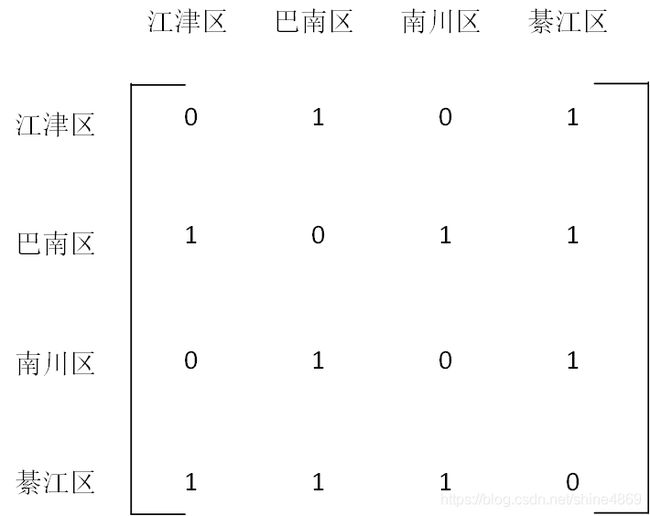
根据公式 S 0 = ∑ i = 1 n ∑ j = 1 n w i j S_{0}=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}w_{ij} S0=i=1∑nj=1∑nwij,此时 n = 4 n=4 n=4,我们可以先将 S 0 S_{0} S0求出来。不难看出, S 0 S_{0} S0其实就是空间权重矩阵中所有元素的和。在这里,这里我们构造的空间权重矩阵对应的 S 0 S_{0} S0为10。
为了后续计算方便,令四个区县的属性值为10,20,30,40,分别对应 y 1 , y 2 , y 3 , y 4 y_{1},y_{2},y_{3},y_{4} y1,y2,y3,y4。则 y ˉ = 25 \bar{y}=25 yˉ=25, ∑ i = 1 4 ( y i − y ˉ ) 2 = 500 \sum\limits_{i=1}^{4}(\mathit{y_{i}}-\bar{\mathit{y}})^{2}=500 i=1∑4(yi−yˉ)2=500
剩下的计算就只有 ∑ i = 1 4 ∑ j = 1 4 w i j ( y i − y ˉ ) ( y j − y ˉ ) \sum\limits_{i=1}^{4}\sum\limits_{j=1}^{4}{w_{ij}(\mathit{y_{i}}-\bar{\mathit{y}})(\mathit{y_{j}}-\bar{\mathit{y}})} i=1∑4j=1∑4wij(yi−yˉ)(yj−yˉ)这一块了。
由于区县自身与自身的空间权重值为0,所以我们只要关注自身与其他区县的相邻情况。考验排列组合的时候到啦,4个区县两两组合,非重复的组合方式共有6( C 4 2 \mathrm{C}_4^2 C42)种。全部列出来如下所示:
江津区与巴南区、江津区与南川区、江津区与綦江区
巴南区与南川区、巴南区与綦江区、南川区与綦江区
以江津区与巴南区为例,其对应得属性值为 y 1 y_{1} y1和 y 2 y_{2} y2,两者相邻故 w 12 = 1 w_{12}=1 w12=1,则 w 12 ( y 1 − y ˉ ) ( y 2 − y ˉ ) = ( 10 − 25 ) ( 20 − 25 ) = 75 w_{12}(y_{1}-\bar{y})(y_{2}-\bar{y})=(10-25)(20-25)=75 w12(y1−yˉ)(y2−yˉ)=(10−25)(20−25)=75
由于 W W W矩阵是对称的(即 w i j = w j i w_{ij}=w_{ji} wij=wji),所以实际上我们在求结果的时候相邻区县只计算一次再乘以2就可以。
以此类推,总的计算总过程如下:
∑ i = 1 4 ∑ j = 1 4 w i j ( y i − y ˉ ) ( y j − y ˉ ) = 2 ∗ ( 10 − 25 ) ( 20 − 25 ) + 2 ∗ ( 10 − 25 ) ( 40 − 25 ) + 2 ∗ ( 20 − 25 ) ( 30 − 25 ) + 2 ∗ ( 20 − 25 ) ( 40 − 25 ) + 2 ∗ ( 30 − 25 ) ( 40 − 25 ) = − 350 \sum\limits_{i=1}^{4}\sum\limits_{j=1}^{4}{w_{ij}(\mathit{y_{i}}-\bar{\mathit{y}})(\mathit{y_{j}}-\bar{\mathit{y}})}=2*(10-25)(20-25)+2*(10-25)(40-25)+2*(20-25)(30-25)+2*(20-25)(40-25)+2*(30-25)(40-25)=-350 i=1∑4j=1∑4wij(yi−yˉ)(yj−yˉ)=2∗(10−25)(20−25)+2∗(10−25)(40−25)+2∗(20−25)(30−25)+2∗(20−25)(40−25)+2∗(30−25)(40−25)=−350
(只有江津区与南川区是不相邻的,故 w 13 = w 31 = 0 w_{13}=w_{31}=0 w13=w31=0)
如果实在不清楚计算过程的话,可以将上述公式全部展开。
最后Global Moran’I的值为:
I = 4 10 × − 350 500 = − 0.28 I=\frac{4}{10}\times\frac{-350}{500}=-0.28 I=104×500−350=−0.28
二、深入理解
从整个计算流程中,我们可知,这个公式之所以能够表示空间单元的相关性,关键还是在于 ∑ i = 1 n ∑ j = 1 n w i j ( y i − y ˉ ) ( y j − y ˉ ) \sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}{w_{ij}(\mathit{y_{i}}-\bar{\mathit{y}})(\mathit{y_{j}}-\bar{\mathit{y}})} i=1∑nj=1∑nwij(yi−yˉ)(yj−yˉ)这一步的计算。实质就是:空间单元的邻接权重指数 × \times ×空间单元间属性值的偏差。前者对应着各地区在空间上的位置关系,后者对应着各地区属性值之间的差异,两者作乘积,再求和,就得到了所有地区在整个空间上的相关性程度。只有当 y i y_{i} yi和 y j y_{j} yj同时大于或者小于 y ˉ \bar{y} yˉ时,莫兰指数才有可能为正;并且当 y i y_{i} yi和 y j y_{j} yj偏离平均值 y ˉ \bar{y} yˉ越大时,莫兰指数的值就越大。
我们联系一下实际情况来深入理解上面这段话的含义。一个教室有很多个座位,一个座位对应一名学生的成绩。 y i y_{i} yi代表 i i i座位学生的成绩, y j y_{j} yj代表 j j j座位学生的成绩。
从聚集的角度来看:
1.当 y i y_{i} yi和 y j y_{j} yj都大(小)于 y ˉ \bar{y} yˉ时,即 i i i座位和 j j j座位的学生成绩都是要高(低)于整个班的平均成绩的,此时如果 i i i座位与 j j j座位相邻,即计算出莫兰指数一定是大于0的。换个方式来说,当莫兰指数大于0时,表示成绩越高(低)的学生越容易聚集在一起。(类比:学霸总和学霸玩,学渣总和学渣玩,此时成绩在空间上呈正相关性)
2.当 y i y_{i} yi和 y j y_{j} yj其中有一个小于平均水平 y ˉ \bar{y} yˉ时,此时如果 i i i座位与 j j j座位相邻,即计算出莫兰指数一定是小于0的。换个方式,当莫兰指数小于0时,表示成绩越高(低)越不容易聚集在一起。(类比:有些学霸特别喜欢和学渣一起玩,此时成绩在空间上呈现负相关性)
3.当一个班上既有学霸和学霸一起玩的现象又有学霸和学渣一起玩的现象时,那么在计算莫兰指数的时候,可能两两抵消,最终莫兰指数为0,那么在整个空间上就表现为不相关性。(但是,其实在部分区域还是出现了聚集现象,这就涉及到局部相关分析的内容了,我们后续再来介绍)
从差异的角度来看:
1.当学霸们和学霸们,学渣们和学渣们都聚集在一起时,那么此时莫兰指数是大于0的,成绩的差异就会变得非常得小。这也就解释了为什么当莫兰指数越大时,空间差异就越小得原因!
2.当学霸们和学渣们聚集在一块时,那么此时莫兰指数小于0,即莫兰指数越小,空间差异就越大。
三、Moran’I指数检验
当然,我们在计算出Moran’I指数之后,不能立马根据其正负,判断其空间相关性。还要对其进行假设检验,看看它是否能通过检验。这里就涉及到假设检验的一些知识,没有学过的小伙伴可参考《统计学》或者《数理统计》等方面的书籍进行了解。
简要介绍一下假设检验的基本步骤:假设检验就是提出一个假设,然后通过计算统计量,按照统计量服从的分布来判断假设是否成立。如果不成立就拒绝这个假设,如果成立则接受这个假设。
当区域个数 n n n足够大时,莫兰指数近似服从正态分布,因此我们可以使用Z检验(也称U检验)对其进行验证。
Z = I − E ( I ) v a r ( I ) Z=\frac{I-E(I)}{\sqrt{var(I)}} Z=var(I)I−E(I)
其均值和方差的计算方法如下所示:
E ( I ) = − 1 n − 1 E(I)=-\frac{1}{n-1} E(I)=−n−11

期望与方差推导可参考文献:MORAN P A P. Notes on continuous stochastic phenomena.[J]. Biometrika,1950,37(1-2).有兴趣的小伙伴可以看下。以后,一般对莫兰指数检测直接都是利用软件计算的,故在此不再以例子进行说明。
特别说明:原假设 H 0 H_{0} H0:所有研究对象在空间上随机分布
在显著性为0.05水平下,只要满足 ∣ Z ∣ > 1.96 |Z|>1.96 ∣Z∣>1.96(或者P值小于0.05)即可拒绝原假设 H 0 H_{0} H0,则有充分理由认为莫兰指数显著。(1.96是正态分布的0.975分位数)
四、R和Geoda计算莫兰指数
计算莫兰指数的软件很多,Arcgis、R、Geoda、python都可以,这里以2018年重庆市各区县人均GDP为基础数据,分别利用R和Geoda计算莫兰指数。
(1)R
注意:
1.在使用readOGR读入shp文件的时候,须保证shp、shx、dbf这三个文件在工作目录下,否则程序会报错!
2.moran.test这个函数的第一个参数必须是数值型向量。以下例子中的数据是因子型,所以通过as.numeric和as.character方法将其转为数值型!
library(rgdal) #负责读入shp文件
library(spdep) #负责计算莫兰指数
rdata=readOGR("Export_Output.shp")
queen_nb=poly2nb(rdata,queen=TRUE) #queen连接的权重矩阵
k4_W=nb2listw(queen_nb) #转为莫兰指数计算所需格式
moran.test(as.numeric(as.character(rdata$PGDP2018)),listw=k4_W) #计算莫兰指数
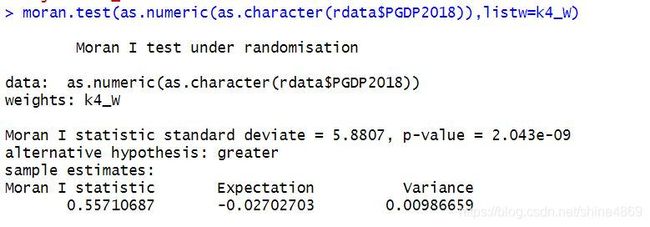
计算得出的Moran’I=0.557,P值为 2.043 × 1 0 − 9 2.043\times10^{-9} 2.043×10−9,远远小于0.05,故
拒绝原假设,有充分理由认为莫兰指数显著有效。
结论:2018年重庆市各区县经济发展水平在空间上呈正相关性,即经济水平越高(低)的地区越容易发生聚集现象
(2)Geoda
相比于R,Geoda的操作就简单很多。载入空间权重矩阵后,点击空间分析——单变量Moran’I分析,选择PGDP2018,如下图所示
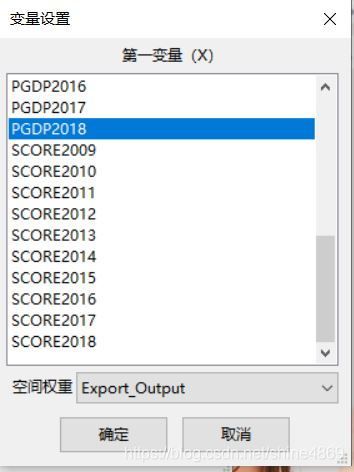
计算出的结果如下图:
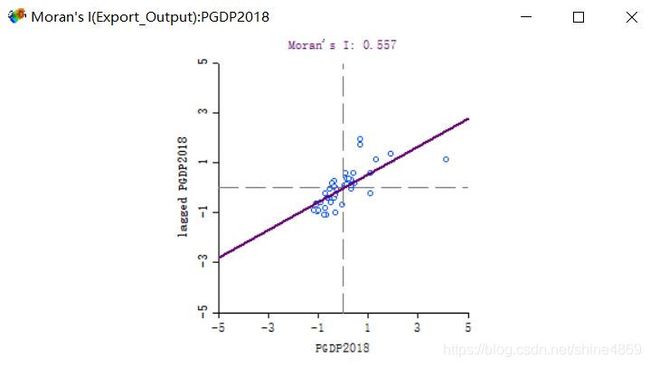
计算得出的Moran’I值也是0.557,和R保持一致。关于这张图的其他细节,会在局部相关分析中进行阐述。
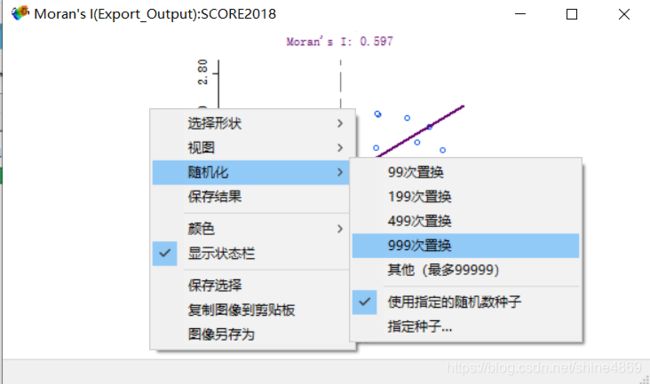
检验方式只需要点击右键选择:随机化——999置换即可(Geoda里进行莫兰指数检验是通过蒙特卡罗的方式计算的,所以尽量把随机次数调高一些)
检验的结果如下:
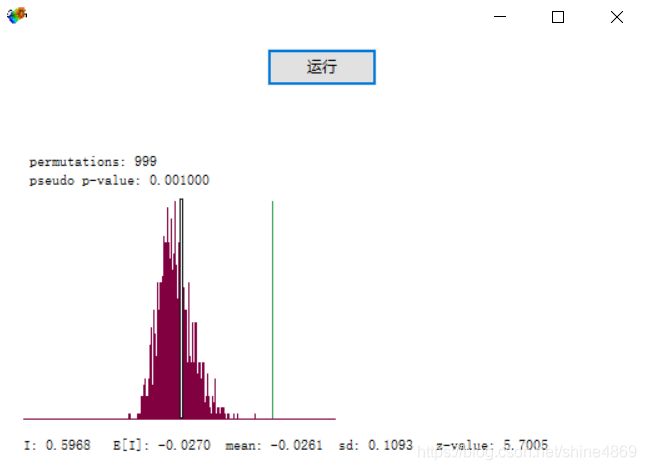
上图的pseudo p-value则是P值,很明显远小于0.05,可以认为moran’I显著有效。(因为是通过正态分布的随机数进行模拟的,所以计算出的moran’I与前面那张图有些许差别。与此同时,通过点击run,会得到不同的均值和方差,但p值始终是不会发生改变的)