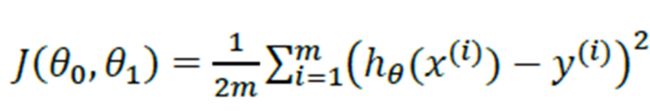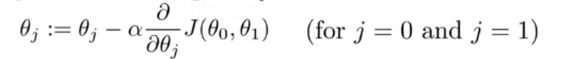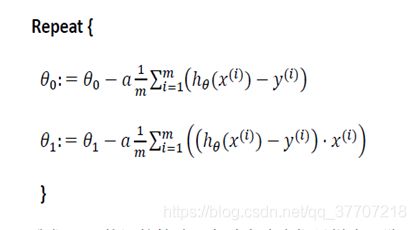单变量线性回归算法分析及python源码
说明：本博客中的分析思路、举例、部分插图等均来源于吴恩达教授在斯坦福大学公开课《机器学习》中的讲解内容！
一、概述
单变量线性回归算法属于监督学习的一类，所谓回归是指我们根据之前的数据预测一个较为准确的输出值。即我们给算法一定的训练集，训练集中的每一个训练样本均为“正确答案”，算法通过对训练集的学习而建立起合适的模型用以预测新的输入值对应的输出值。
二、从一个例子说起
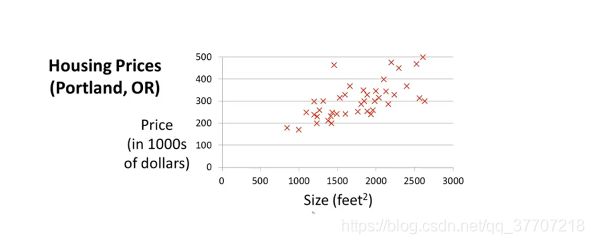
在斯坦福公开课中，通过这么一个例子引入单变量线性回归算法的问题，即“根据房子面积预测房子售价”。如图2.1所示，我们已知一组数据集，数据集中的数据描述了房屋面积与价格的对应关系，且该数据集中的每一个样本都是正确的。我们现在要做的就是根据已有训练集去建立起一个合适的模型，让我们可以通过这个模型去预测一些数据集中所没有的房屋面积对相应的房屋价格。在单变量线性回归算法中，这个所谓的“模型”便是一条“一元一次方程”直线。因此，通俗的讲，我们要做的就是寻找一条与已有数据集尽量拟合的一元一次方程。这里要提到一点，所谓“回归”与“拟合”并不完全等同，但作为初学者来说难以对两者进行明确的区分，且个人认为，在初学阶段，用“拟合”来帮助理解“回归”并无不妥。至于两者间的区别可参考文章线性回归中“回归”的含义，文章作者从历史发展的角度解读了“拟合”与“回归”。
图2.1 面积-价格对应离散图
三、获得模型的宏观过程
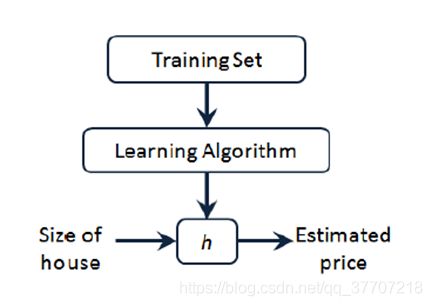
根据上述可以知道,我们所要建立的模型形式为一元一次方程，我们不妨将其设为h(x)=θ0+ θ1 *x，h(x)称为“假设（hypothesis）”，也就是我们要求的模型。设置好假设形式后，我们从更宏观的角度看一下我们得到最终h(x)的整个过程。如图3.1所示，我们将训练集(Training Set)输入学习算法(Learning Algorithm)，经过训练之后得到假设h(x)。然后，我们便可通过假设h(x)对其他面积的房屋价格进行预测。
图3.1 宏观过程
四、对“假设”拟合程度的考察——代价函数（cost function）
在二维平面上有着无数条一元一次方程直线，那么该如何判断哪条直线是最合适、是跟训练集拟合程度最高的呢？这里就引入了“代价函数”的概念。顾名思义，一条直线的代价函数所描述的是“用这条直线代替训练集中的点后引起的误差”，我们将这个“误差”称为“代价”。
我们首先引入代价函数的形式，再对代价函数进行分析。代价函数形式如图4.1。
图 4.1 代价函数的形式
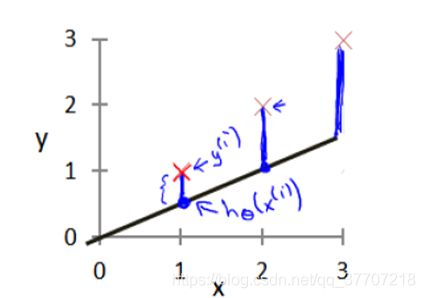
图中，x^(i)代表训练集中第i个样本的输入值，y^(i)代表训练集中第i个样本的输出值，hθ (x^(i))代表“假设函数对应于训练集中第i个样本输入值的输出值”，m代表训练样本的数量。在整个代价函数的公式中，不可知的量只有θ0与 θ1，也就是最终决假设函数的两个量。为了更直观的理解该公式，我们引入图4.2
图 4.2
在图4.2中，×所对应的坐标即为x^(i)与y^(i)，由×向x轴做垂线，垂线与斜线的交点对应的y轴坐标即为hθ (x^(i))，因此公式中的“hθ(x^(i))-y^(i)”就是用拟合直线值代替离散值后在第i个样本处引起的误差。那么明显可以看出，代价函数所求的是“用拟合直线代替离散点后在所有训练样本处引起的误差的平方和的均值”。当该代价函数值越小，说明假设函数与训练集的拟合程度越高，也就是说假设函数越“合适”。
接下来的思路就很明确了——求代价函数的极小值点，将代价函数在极小值点对应的θ0与 θ1代入假设，就可以得到拟合程度最高的假设函数了。值得强调的是，代价函数公式中，求和符号前面乘了1/2m，而求误差均值的应该乘1/m，这里纯粹是为了后续计算方便。实际上，我们接下来的操作是求代价函数的极小值点，所以在求和符号前乘以任意一个不为零的常数都对求代价函数的极小值点是没影响的。
五、求代价函数极小值点——梯度下降算法
（一）梯度下降算法的形象理解
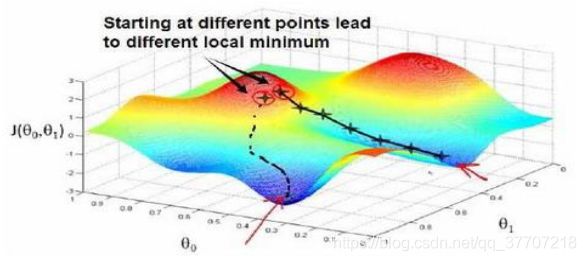
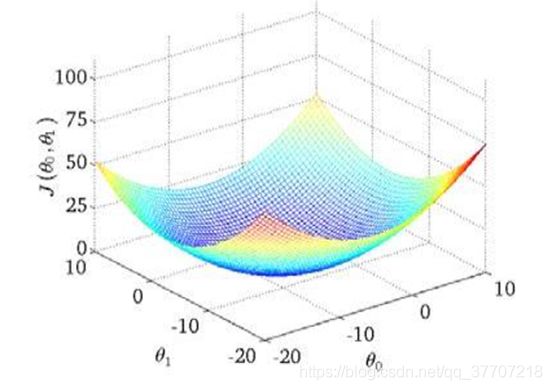
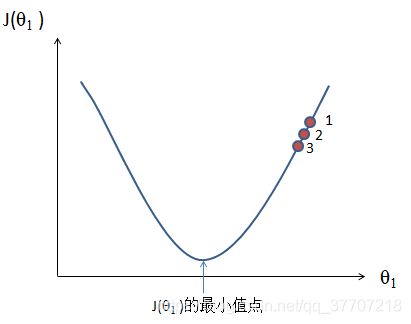
在求代价函数极小值的过程中用到了“梯度下降”算法，我们可以用下山来比较形象的理解梯度下降的原理：我们首先选定山上的某一点作为起点，然后环视四周，选择一个能让自己高度下降的方向向前走一步，然后重复上述过程，那我们就能逐步的到达山的最低点。但很明显的是，梯度下降算法存在一定的缺陷，即当我们选定的初始点不同时，到达的最低点也可能不同，即我们的算法可能陷入局部极小值点而无法到达全局极小值点或者说最小值点，如图5.1所示。但是在单变量线性回归算法中，我们的代价函数图像是一个凹图像，如图5.2所示，因此在本文章中就可以暂且不考虑这个问题。
图 5.1
图 5.2
与此同理，首先我们随意给定θ0与θ1 一个初始值，然后不断迭代执行梯度下降算法，最终即可到达代价函数的最小值点。
（二）梯度下降算法的公式及分析
首先引入单变量线性回归算法中梯度下降公式，如图5.3
图5.3
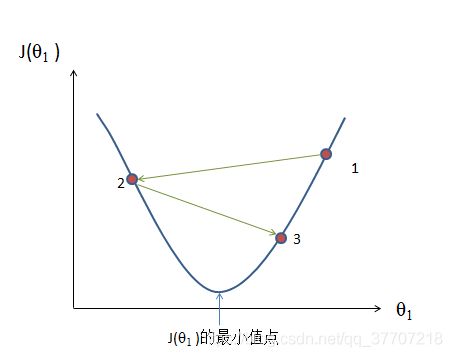
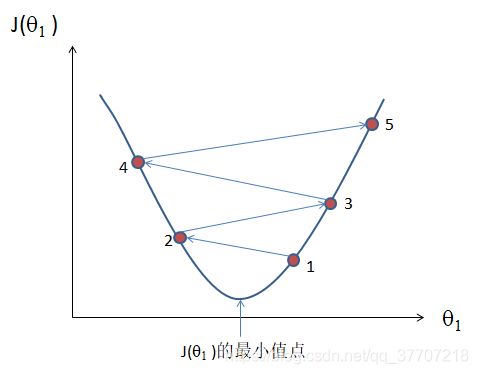
公式中的为正数，它代表是学习率，决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，他的选择也是十分重要的。接下来通过图片说明梯度下降算法为什么可以使我们到达代价函数最小值点，以θ1为例进行说明，如图5.4
图 5.4
假设θ1的起始点在1处，则其导数为正数，因为学习率也为正数，则经过梯度下降公式后，θ1的值更新为“其自身减去一个正数”，也就是说变小了，那么有可能跳到了点2；再次应用梯度下降公式，因为点2处为负数而学习率为正数，那么θ1的值更新为“其自身减去一个负数”，也就是说变大了，那么有可能跳到了点3；如此反复进行，则从x轴来看，θ1的值在一次次运用梯度下降公式的过程中逐步接近了代价函数的极小值点，这就达到了我们的目的。
（三）学习率的选择
在上一部分说到学习率的选择十分重要，因为学习率决定了函数将以怎样的速度逼近最小值点，所以合适的学习率能保证函数在不出问题的前提下以最快的速度到达最小值点，减少程序迭代次数。接下来将通过两个极端情况的例子来说明学习率选择中可能出现的问题：
当学习率过小时，函数仍然能逼近最小值点，但逼近速度非常慢，需要更多的迭代次数，也就意味着程序计算量加大，运行速度减慢，如图5.5
图 5.5
当学习率过大时，可能会导致θ1变化幅度过大，导致其在最小值点两边震荡甚至距离最小值点越来越远，如图5.6
图 5.6
对我而言，我喜欢用的方式是先将学习率设为一个较小的值（如：0.00001），然后画出代价函数图像，只要代价函数图像是“单调不增”’的，那么就将学习率改为原来的三倍，再次观察代价函数图像，如此反复，最终选择那个能让代价函数保持单调不增的最大的学习率作为最终学习率。
（四）同步更新问题
因为单变量线性归回算法中涉及到了两个未知数θ0与 θ1，因此上述的梯度下降算法要应用到两个未知量之上，如图5.7
图 5.7
但该公式实际上是存在问题的，在执行完第一条之后，θ0的值已经改变，再执行第二条时，第二条公式中θ0的值已经不是初始值，这样就相当于先更新了θ0的值后更新了θ~1~的值，且先更新的θ0对后更新的θ1产生了影响。因此，我们应对两个未知量进行同步更新，如图5.8
图 5.7
六、单变量线性回归算法的Python实现
（一）产生训练集
采用随机函数产生50个1到300的不重复的随机数作为训练集中y的值，50个1到300的不重复的随机数作为训练集中x的值
import random #提供random.sample函数
x=random.sample(range(1,300),50)
y=random.sample(range(1,300),50) #采用sample抽样的方式即可达到不重复的目的
（二）排序
对x与y进行排序，使离散点大概复合一元一次方程形式
x.sort()
y.sort()（三）实现梯度下降算法，假设h(x)=ax+b
k=0.00001 #学习率
i=1 #记录迭代次数
j=0 #用于求和次数
sum=0 #用于记录求和值
temp_a=[] #记录a每次迭代后的值
temp_b=[] #记录b每次迭代后的值
J=[] #记录每次迭代后的代价函数值
a=b=5 #a与b的初始值
temp_a.insert(0,5) #给记录a,b变化的数组初值赋为5
temp_b.insert(0,5)
while j<=49: #计算代价函数值初始值
sum+=(a*x[j]+b-y[j])**2
j+=1
sum/=100
J.insert(0,sum)
while i<=100: #通过循环进行100次迭代
j=0 #设置初始值
sum=0
while j<=49: #计算a迭代后的数值
sum+=(a*x[j]+b-y[j])*x[j]
j+=1
sum/=50
temp_a.insert(i,a-k*sum)
j=0 #设置初始值
sum=0
while j<=49: #计算b迭代后的数值
sum+=(a*x[j]+b-y[j])
j+=1
sum/=50
temp_b.insert(i,b-k*sum)
a=temp_a[i] #同步更新
b=temp_b[i]
j=0 #设置初始值
sum=0
while j<=49: #计算迭代后的代价函数值
sum+=(a*x[j]+b-y[j])**2
j+=1
sum/=100
J.insert(i,sum)
i+=1 #迭代次数加1（四）绘制图像
import numpy as np
import matplotlib.pyplot as plt
colors1 = '#00CED1' #点的颜色
##(1)画代价函数的图
plt.figure()
plt.xlabel('times')
plt.ylabel('J(a,b)')
i=np.linspace(0,100,101)
area = np.pi * 2**2 # 点面积
plt.plot(i,J,'-r',label='cost function')
plt.legend() #给图像加图例，图例格式默认
##(2)画训练集和拟合直线的图########
plt.figure()
plt.xlabel('X')
plt.ylabel('Y')
plt.xlim(xmax=300,xmin=0)
plt.ylim(ymax=300,ymin=0)
plt.scatter(x, y, s=area, c=colors1, alpha=0.4, label='Training set')# 画训练集与假设图（五）最终代码及运行结果
#####1.采用随机函数产生50个1到300的不重复的随机数作为训练集中y的值，50个1到300的不重复的随机数作为训练集中x的值#####
import random #提供random.sample函数
x=random.sample(range(1,300),50)
y=random.sample(range(1,300),50) #采用sample抽样的方式即可达到不重复的目的
#####2.对x与y进行排序，使离散点大概复合一元一次方程形式##########################################################与y进行排序，使离散点大概复合一元一次方程形式##########################################################
x.sort()
y.sort()
#####3.实现算法，假设h(x)=ax+b#####################################################################################
k=0.00001 #学习率
i=1 #记录迭代次数
j=0 #用于求和次数
sum=0 #用于记录求和值
temp_a=[] #记录a每次迭代后的值
temp_b=[] #记录b每次迭代后的值
J=[] #记录每次迭代后的代价函数值
a=b=5 #a与b的初始值
temp_a.insert(0,5) #给记录a,b变化的数组初值赋为5
temp_b.insert(0,5)
while j<=49: #计算代价函数值初始值
sum+=(a*x[j]+b-y[j])**2
j+=1
sum/=100
J.insert(0,sum)
while i<=100: #通过循环进行100次迭代
j=0 #设置初始值
sum=0
while j<=49: #计算a迭代后的数值
sum+=(a*x[j]+b-y[j])*x[j]
j+=1
sum/=50
temp_a.insert(i,a-k*sum)
j=0 #设置初始值
sum=0
while j<=49: #计算b迭代后的数值
sum+=(a*x[j]+b-y[j])
j+=1
sum/=50
temp_b.insert(i,b-k*sum)
a=temp_a[i] #同步更新
b=temp_b[i]
j=0 #设置初始值
sum=0
while j<=49: #计算迭代后的代价函数值
sum+=(a*x[j]+b-y[j])**2
j+=1
sum/=100
J.insert(i,sum)
i+=1 #迭代次数加1
#####4.开始画图################################################################################################
import numpy as np
import matplotlib.pyplot as plt
colors1 = '#00CED1' #点的颜色
##(1)画代价函数的图
plt.figure()
plt.xlabel('times')
plt.ylabel('J(a,b)')
i=np.linspace(0,100,101)
area = np.pi * 2**2 # 点面积
plt.plot(i,J,'-r',label='cost function')
plt.legend() #给图像加图例，图例格式默认
##(2)画训练集和拟合直线的图########
plt.figure()
plt.xlabel('X')
plt.ylabel('Y')
plt.xlim(xmax=300,xmin=0)
plt.ylim(ymax=300,ymin=0)
plt.scatter(x, y, s=area, c=colors1, alpha=0.4, label='Training set')# 画训练集与假设图
n=np.linspace(0,300,1500) #在0~300间均匀取1500个数据
m=a*n+b
plt.plot(n,m,'-r',label='h(x)')
plt.legend() #给图像加图例，图例格式默认
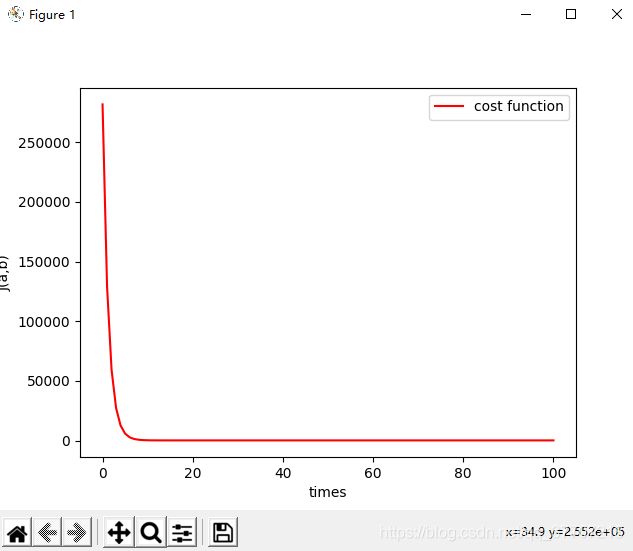
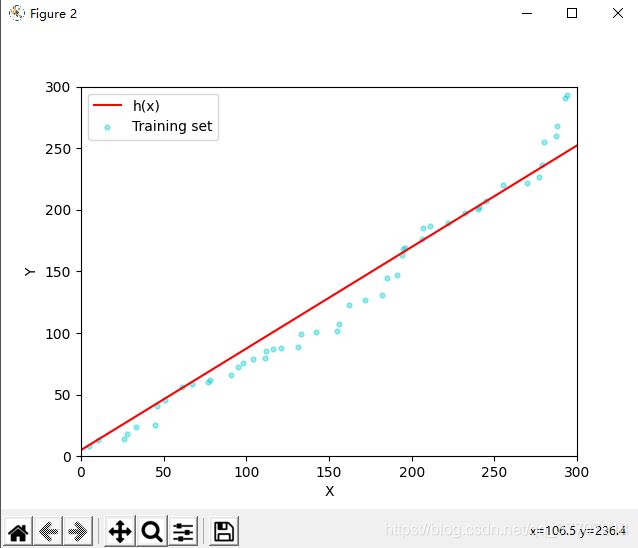
plt.show()代价函数与拟合结果如图6.1、6.2所示
图6.1 cost function
图6.2 Simple linear regression
左肩理想右肩担当，君子不怨永远不会停下脚步！