排序算法总结_python实现
1 冒泡排序
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定排序法
lt = [2,4,3,7,9,6,1]
def dubble_sort(lt):
print(f"输入数组:{lt}")
for i in range(len(lt)-1):
flag = 0
for j in range(len(lt)-1-i):
if lt[j] > lt[j+1]:
lt[j],lt[j+1] = lt[j+1],lt[j]
flag += 1
if flag == 0:
break
print(f"第{i}次排序结果:{lt}")
dubble_sort(lt)
2 选择排序
描述:找到某一位为基准,依次向后如果比这个数小就交换,这样即可将最小数放到当前基准上。
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定排序法
def select_sort(data):
for i in range(len(data)-1):
for j in range(i+1, len(data)):
if data[i] > data[j]:
data[i], data[j] = data[j], data[i]
print(f"第{i}次排序结果:{data}")
data = [2,4,3,7,9,6,1]
select_sort(data)
3 插入排序
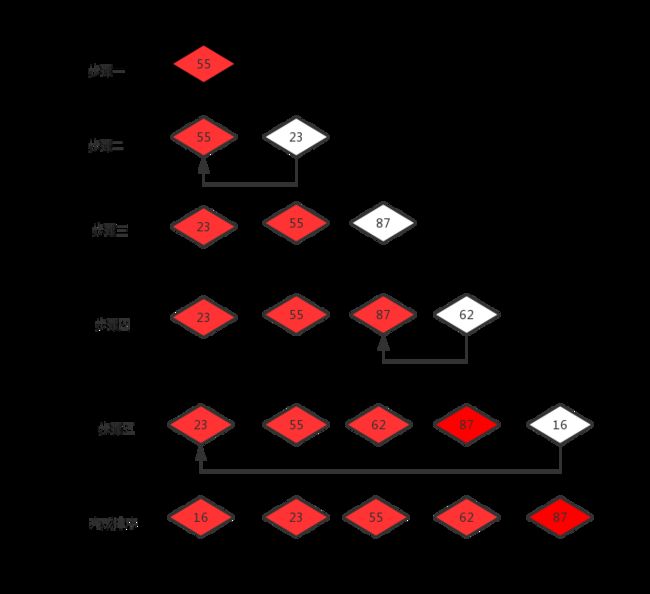
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定排序法
3 快速排序
def sort_quick(array, l, r):
if l < r:
q = patition(array, l, r)
sort_quick(array, 1, q-1)
sort_quick(array, q+1, r)
def patition(array, l, r):
x = array[r]
i = l - 1
for j in range(l,r):
if array[j] < x:
i += 1
array[i], array[j] = array[j], array[i]
array[i+1], array[r] = array[r], array[i+1]
return i + 1
array = [2,4,3,7,9,6,1]
quick_sort(array,0,len(array)-1)
array
4 归并排序
归并排序参考:https://blog.csdn.net/hellojoy/article/details/81835559
def merge(a, b):
c = []
h = j = 0
# 开始有序数组合并,直到有一个先结束
while j < len(a) and h < len(b):
if a[j] < b[h]:
c.append(a[j])
j += 1
else:
c.append(b[h])
h += 1
# 找到先结束的数组,将未结束的放到结果末尾
if j == len(a):
for i in b[h:]:
c.append(i)
else:
for i in a[j:]:
c.append(i)
return c
def merge_sort(lists):
if len(lists) <= 1:
return lists
middle = len(lists)/2
left = merge_sort(lists[:middle])
right = merge_sort(lists[middle:])
return merge(left, right)
array = [2,4,3,7,9,6,1]
quick_sort(array,0,len(array)-1)
array

