Hungarian Algorithm匈牙利算法

匈牙利算法简介

匈牙利算法是一种在多项式时间内（ O(n3) ）求解任务分配问题的组合优化算法。它之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家的工作之上创建起来的。此后该算法被称为Kuhn–Munkres算法或Munkres分配算法（The Munkres Assignment Algorithm）。

接下来，我们将举例介绍这个算法。

问题的引入

首先，我们来考虑一个问题。

假设你是一个网络服务的供应商，你们可以免费给用户装Wi-Fi。现在呢，有三家用户要装Wi-Fi，同时，你有三个装Wi-Fi的工人在附近。

注：

• Job —> 装Wi-Fi
• Worker —> 工人

每个工人前往用户家装Wi-Fi需要一定开销（比如，油费，车费等等）。开销见下图。

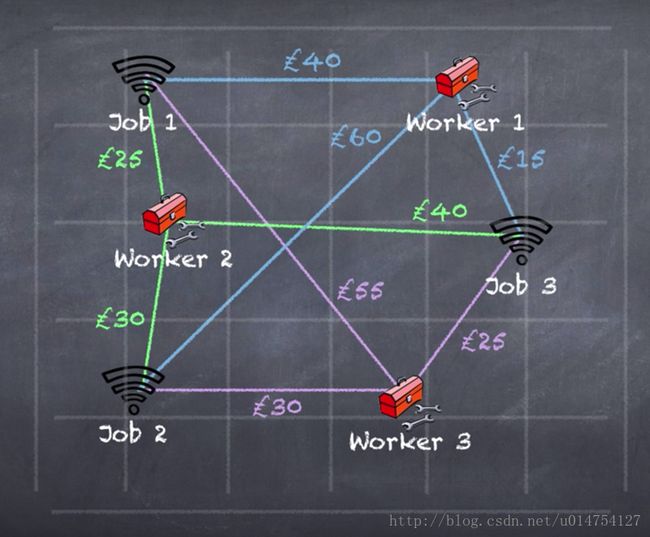
用矩阵表示为

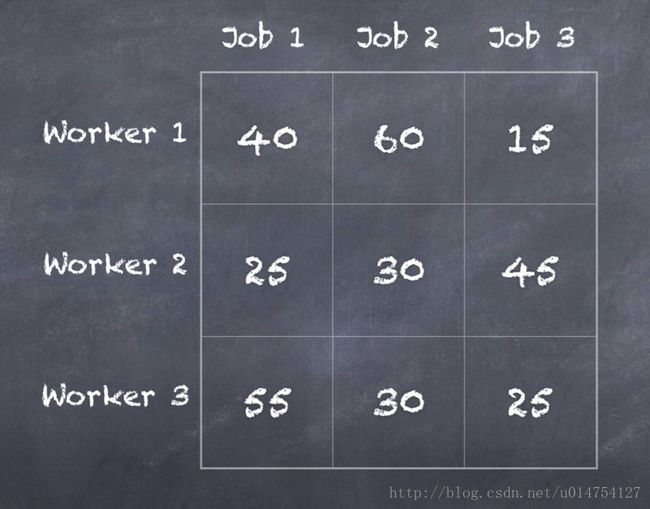
作为一个商人，你肯定想的是，要怎么分配可以最省钱呢？你会通过比较不同分配方案的开销，选择最省钱的那个作为分配方案。

注意：分配时，每个工人只安装一户人家的Wi-Fi。

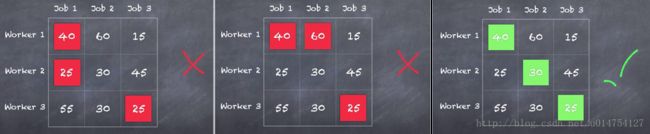
对于每一个分配方案，我们都可以计算出它的总开销。在这个问题中，一共有6种分配方案，如下图所示。

我们最终选择总开销最小的方案，即第4个方案。最小总开销为70。

现在，找到了最小开销的分配方案，解决了问题。但你是不是觉得，这样算起来特别麻烦呢？

现在是一个 3×3 的矩阵， n=3 ，如果 n=1000，10000 呢？

一共要计算 n×(n−1)×(n−2)×…×1 次，时间效率是 O(n!) 。这太糟糕了！

为了更高效地解决这个问题，我们是时候搬出匈牙利算法了。

用匈牙利算法求解任务分配问题（一）

好，我们来看看匈牙利算法是怎么解决这个问题的。

第一步：Row reduction

每一行减去这一行的最小值。

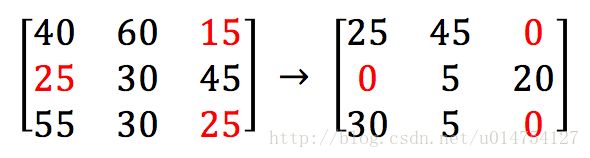
那么现在每一行至少有一个0。

第二步：Column reduction

每一列减去这一列的最小值。

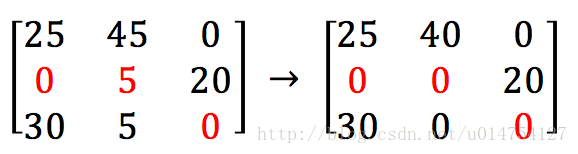
好，现在每一列至少有一个0。

第三步：Test for an optimal assignment

这一步，我们要用最少的直线把矩阵中的零都给覆盖了。

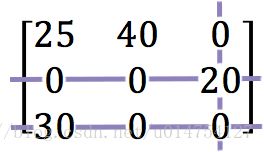
如果直线的数量 =n ，那我们就可以得到一个最优方案了。那就直接跳过第4步，直达第5步。

在这个例子里，最少直线数 =3=n ，我们就可以直达第5步了。

第五步：Making the final assignment

我们选择3个不在同一行，同一列的0就行。被选择的这些0代表了最终的分配方案。即，

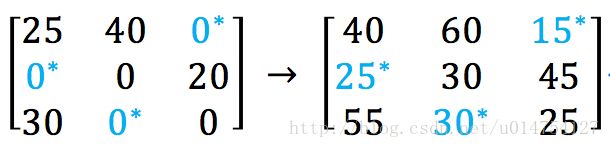
当第三步最少直线数 <n 时呢？
我们换一个例子来说明。

用匈牙利算法求解任务分配问题（二）

第一步：Row reduction

每一行减去这一行的最小值。

那么现在每一行至少有一个0。

第二步：Column reduction

每一列减去这一列的最小值。

好，现在每一列至少有一个0。

第三步：Test for an optimal assignment

这一步，我们要用最少的直线把矩阵中的零都给覆盖了。

这次，最少直线数 =2<3 ，那么我们转入第四步。

第四步：Shift zeros

我们需要至少转移一个 0 到直线未覆盖的位置，来增加覆盖 0 的最少直线数。

首先，我们找出没被直线覆盖的值中的最小值。

在本例中为5。

接下来，每个未被直线覆盖的值都减去这个最小值。然后在直线交叉处加上这个最小值。

最后我们把直线移除，回到第三步。

第三步：Test for an optimal assignment

这一步，我们要用最少的直线把矩阵中的零都给覆盖了。

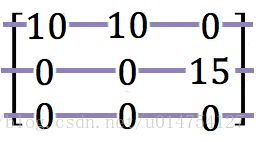
这次，最少直线数 =3=n ，那么我们转入第五步。

第五步：Making the final assignment

我们选择 3 个不在同一行，同一列的 0 就行。被选择的这些0代表了最终的分配方案。你可能会找到不同的分配方案。

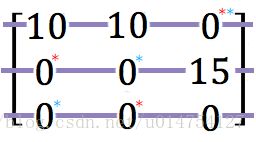
这些方案都是可行的，它们的开销都等于最小开销。即，

15+20+10=25+10+10=45

用匈牙利算法求解任务分配问题（三）

还有一个问题，如果工人数和任务数不相同呢？我们该怎么用匈牙利算法？

答：
我们只需要用0填充缺失的行或列就行。然后记得在第五步确定最终分配方案时，把它们移除。

匈牙利算法时间复杂度分析

下面我们来分析一下匈牙利算法的时间复杂度。

该算法整体流程如下：

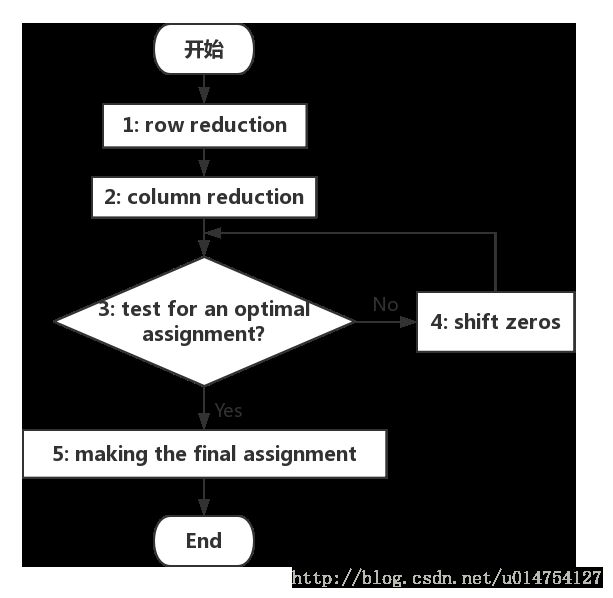
第一步和第二步对矩阵中元素进行了扫描和更新。由于矩阵中一共有 n2 个元素，则这两步的时间复杂度均为 O(n2)

第三步是用直线覆盖所有零元素，因此该步需要访问所有零元素，其中零元素个数最多达 n2 。

第四步需要扫描和更新矩阵中的元素，最多 n2 个。

因此第三步，第四步均为 O(n2) 。

但是第三，四步需要迭代进行，直到最少直线数等于 n 时，停止迭代。每一次迭代，最少直线数都会至少增加1条，因此最多迭代次数为 n 次。

因此，第三步，第四步时间复杂度最高为 O(n3) 。

第五步得到最终分配方案，时间复杂度为 O(n) 。

因此匈牙利算法的时间复杂度为 O(n3) 。