机器学习 (一): 单变量线性回归

前言

线性回归( Linear Regression )是指将一个因变量 $y$ 和多个自变量$x_1,x_2...x_n$的关系用一个线性方程:

$y=B+W_1{x}_1+W_2{x}_2...+W_3{x}_3$

拟合出来. 本篇先介绍最简单的单变量线性回归, 即将两个变量 $y$ 和 $x$用一个一元线性方程

$y=B+Wx$

来拟合.

模拟数据

我的想法是是, 先自定义一个要被拟合的线性关系, 然后通过机器学习来计算出该关系.
要被拟合的线性关系为:

$y=B^{\prime }+x{W}^{\prime }+E$

其中 $B^{\prime }$ 和 $W^{\prime }$是待拟合的系数, E是一个随机数, 从而给数据添加一些随机性

代码

#coding:utf-8

sampleCount = 100 #模拟数据的数量
sampleX = [] #模拟数据的 x 值
sampleY = [] #模拟数据的 y 值

def showRaw():
	SEED = 0 #随机数种子
	W_ = 5.75 #模拟数据的系数 W'
	B_ = 30 #模拟数据的偏移量 B'
	E_ = 100 #模拟数据的随机偏差(取值范围为 ± E/2)

	# 模拟数据的点集
	random.seed(SEED)
	for i in range(sampleCount):
		x = random.random() * 250
		y = W_ * x + B_ + (random.random() - 0.5) * E_
		sampleX.append(x)
		sampleY.append(y)

	# 模拟数据的线性关系
	ansX = np.linspace(0, 250, 250)
	ansY = ansX * W_ + B_
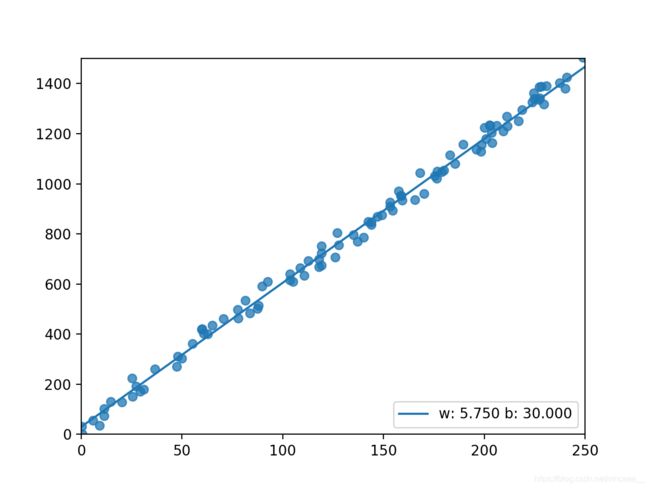
	plt.plot(ansX, ansY, label=('w: %.3f b: %.3f')%(W_, B_))
	
	plt.scatter(sampleX, sampleY, alpha = 0.75)
	plt.xlim(0, 250)
	plt.ylim(0, 1500)

showRaw()

图示

梯度下降

本篇的机器学习算法是梯度下降.

误差函数

首先我们定义一个误差函数.
误差函数用来评估一个拟合关系的优劣, 对于一组数量为 $m$ 的数据集, 和一个
$h_{W,B}(x)=Wx+B$
拟合函数, 该函数的误差函数为:

$J(W,B)=\frac{1}{2m}\sum _{i=1}^m(h_{W,B}(x_i)-y{)}^2$

即拟合值和真实数据的方差除以二, 用方差而不是绝对值差或者标准差的原因是方差全局可导, 除以二的意义是求导的时候可以约去.

可以看出, 该函数有两个自变量$W$和$B$, 他们分别的偏导数为:

$J_W^{\prime }=\frac{1}{m}\sum _{i=1}^m[(h_{W,B}(x_i)-y(i)\ast x_i]$

$J_B^{\prime }=\frac{1}{m}\sum _{i=1}^m(h_{W,B}(x_i)-y(i))$

因此, 我们的目标是, 找出一个二元组 $(W,B)$ 使得 $J_W^{\prime }$ 和 $J_B^{\prime }$ 均小于 $ϵ$, 其中 $ϵ$ 为一个非常小的值 (我自己定义的是 $0.001$). (因为这是计算机世界, 取值是离散的, 所以很难做到偏导数等于 $0$ ).

计算偏导数

梯度下降听起来牛逼, 实际上是通过计算误差函数的 偏导数 来得到最优的参数 $W$ 和 $B$ 从而得到最小的误差.
高中的时候我们学过一个函数 $f(x)$ 的 极小(大)值 的位置是它在 $f^{\prime }(x)=0$时对应的 $x$ 值. 梯度下降就是这个思想.
好消息是, 线性回归的误差函数只有一个全局最小值, 因此不存在其它的局部极小值.

代码

# 返回 J(W, B)分别在W = w 和 B = b时的偏导数值
def getDerivative(w, b):
	dw = 0
	db = 0
	for i in range(sampleCount):
		dw += (w * sampleX[i] + b - sampleY[i]) * sampleX[i] * 1.0 / sampleCount
		db += (w * sampleX[i] + b - sampleY[i]) * 1.0 / sampleCount
	return (dw, db)

调整参数

每次取

$W^{\prime }=W-\alpha J_W^{\prime }(W,B)$

$B^{\prime }=B-\alpha J_B^{\prime }(W,B)$

其中 $\alpha$ 的学名叫学习率, 即每次参数变化的幅度

• $\alpha$ 太大可能会导致无法收敛
• $\alpha$ 太小会导致收敛速度太慢

因此这个 $\alpha$ 得自己手动试, 哎.

代码

def linearRegression():
	W = 1.0 #随便设置的一个初始 W
	B = 1.0 #随便设置的一个初始 B
	a = 0.000085 #学习率
	dw, db = getDerivative(W, B)
	while abs(dw) > EPSILON or abs(db) > EPSILON:
		W -= dw * a
		B -= db * a
		dw, db = getDerivative(W, B)

	#画出来
	x = np.linspace(0, 250, 250)
	y = x * W + B
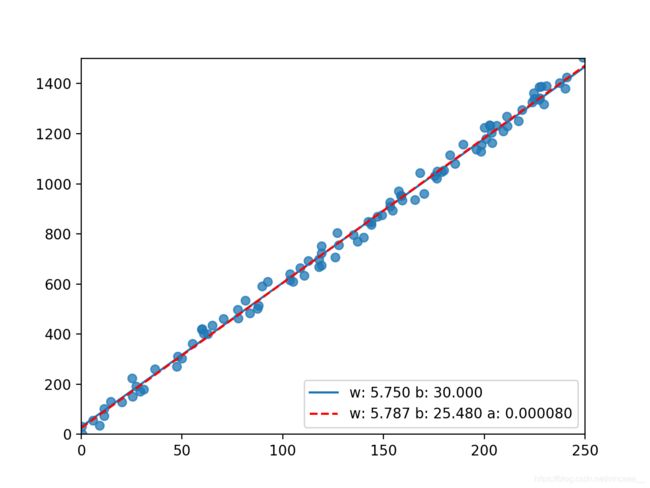
	plt.plot(x, y, color = 'red', linestyle='--', label=('w: %.3f b: %.3f a: %f')%(W, B, a))

图示 (红色虚线为拟合函数)

全部代码

import numpy as np 
import matplotlib.pyplot as plt 
import random

sampleCount = 100
sampleX = []
sampleY = []

EPSILON = 0.001

def showRaw():
	SEED = 0
	W_ = 5.75
	B_ = 30
	E_ = 100

	ansX = np.linspace(0, 250, 250)
	ansY = ansX * W_ + B_

	random.seed(SEED)
	for i in range(sampleCount):
		x = random.random() * 250
		y = W_ * x + B_ + (random.random() - 0.5) * E_
		sampleX.append(x)
		sampleY.append(y)

	plt.scatter(sampleX, sampleY, alpha = 0.75)
	plt.plot(ansX, ansY, label=('w: %.3f b: %.3f')%(W_, B_))
	plt.xlim(0, 250)
	plt.ylim(0, 1500)

def getDerivative(w, b):
	dw = 0
	db = 0
	for i in range(sampleCount):
		dw += (w * sampleX[i] + b - sampleY[i]) * sampleX[i] * 1.0 / sampleCount
		db += (w * sampleX[i] + b - sampleY[i]) * 1.0 / sampleCount
	result = (dw, db)
	print("w: %f, b: %f " % (w, b) + str(result))
	return result



showRaw()
linearRegression()
plt.legend(loc='lower right')
plt.show()

总结

所谓 机器学习 是这样的一种算法: 该算法的性能会随着训练数据的增多而上升, 而本篇介绍的线性回归 (梯度下降) 为一个典型的机器学习的算法, 算是机器学习的 hello world吧~