openCV 中值滤波算法解析
中值滤波算法是使用一个模板,在图像中移动的过程中,取模板内的排列中间的值替代模板中心的值。
常用的中值滤波的快速算法见论文“A Fast Two-Dimensional Median Filtering Algorithm”。本人按照论文上的方法实现了一下,发现效率仅是openCV的十分之一,研究了一下openCV1.0的源码,发现他也是用的论文上的原理,但是,他的编程手法就高明多了。下面,咱们就看一下openCV是怎么处理的!
/*
1.src原图
2.src_step原图步长
3.dst处理后
4.dst图步长
5.size 图像大小
6.m模板大小
7.cn图像通道数
*/
static CvStatus CV_STDCALL icvMedianBlur_8u_CnR( uchar* src, int src_step, uchar* dst, int dst_step, CvSize size, int m, int cn )
{//定义16级灰度直方图
#define N 16
int zone0[4][N];
//定义256级灰度直方图int zone1[4][N*N];
int x, y;
int n2 = m*m/2;
int nx = (m + 1)/2 - 1;
uchar* src_max = src + size.height*src_step;
uchar* src_right = src + size.width*cn;
//更新直方图
#define UPDATE_ACC01( pix, cn, op ) \
{ \
int p = (pix); \
zone1[cn][p] op; \
zone0[cn][p >> 4] op; \
}
if( size.height < nx || size.width < nx )
return CV_BADSIZE_ERR;
//模板大小为3时候,单独处理(效率高)
if( m == 3 ){
size.width *= cn;
for( y = 0; y < size.height; y++, dst += dst_step )
{
const uchar* src0 = src + src_step*(y-1);
const uchar* src1 = src0 + src_step;
const uchar* src2 = src1 + src_step;
//处理第一列的时候src0 = src1
if( y == 0 )src0 = src1;
//处理最后一列的时候 src2 = src1
else if( y == size.height - 1 )src2 = src1;
//考虑多通道循环
for( x = 0; x < 2*cn; x++ )
{
int x0 = x < cn ? x : size.width - 3*cn + x;
int x2 = x < cn ? x + cn : size.width - 2*cn + x;
int x1 = x < cn ? x0 : x2, t;
int p0 = src0[x0], p1 = src0[x1], p2 = src0[x2];
int p3 = src1[x0], p4 = src1[x1], p5 = src1[x2];
int p6 = src2[x0], p7 = src2[x1], p8 = src2[x2];
CV_MINMAX_8U(p1, p2); CV_MINMAX_8U(p4, p5);
CV_MINMAX_8U(p7, p8); CV_MINMAX_8U(p0, p1);
CV_MINMAX_8U(p3, p4); CV_MINMAX_8U(p6, p7);
//代码图解:0~5代表执行顺序,
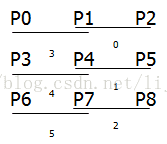
CV_MINMAX_8U(p1, p2); CV_MINMAX_8U(p4, p5);
CV_MINMAX_8U(p7, p8); CV_MINMAX_8U(p0, p3);
CV_MINMAX_8U(p5, p8); CV_MINMAX_8U(p4, p7);
//代码图解:0~5代表执行顺序,
//经过第一步六次对比,再加上本次的0~2的三次对比,3*3的数据已经达到行向有序(从小到大)
//P0 P3 P6 是行向最小值 ,P2 P5 P8 是行向最大值
CV_MINMAX_8U(p3, p6); CV_MINMAX_8U(p1, p4);CV_MINMAX_8U(p2, p5); CV_MINMAX_8U(p4, p7);
CV_MINMAX_8U(p4, p2); CV_MINMAX_8U(p6, p4);
//代码图解:0~5代表执行顺序,
//经过第二步的六次对比,再加上本次的0~3的四次对比,中间列(P1、P4、P7)已到达列向有序,第一列和第三列都没有严格有序
//但是,可以确定的是P6是行向小值和列向最大值, P2 是行向最大值和列向最小值

CV_MINMAX_8U(p4, p2);
//第三部经过4~5两次斜向对比,再加上本步一次对比,实现了(P2、P4、P6)的斜向有序。
//对比完成后P4就是中值
//总之,其算法的基本思路是先对数据进行排序(算法中的行向有序),然后再在三组有序的数据中找到数据合并后的中位数
//那就是,取出有序序列组的最小值中的最大值、最大值中的最小值、中间列向的中值,三个数进行比较,取其中值就是
//三个有序序列的中值
dst[x1] = (uchar)p4;}
for( x = cn; x < size.width - cn; x++ )
{
int p0 = src0[x-cn], p1 = src0[x], p2 = src0[x+cn];
int p3 = src1[x-cn], p4 = src1[x], p5 = src1[x+cn];
int p6 = src2[x-cn], p7 = src2[x], p8 = src2[x+cn];
int t;
CV_MINMAX_8U(p1, p2); CV_MINMAX_8U(p4, p5);
CV_MINMAX_8U(p7, p8); CV_MINMAX_8U(p0, p1);
CV_MINMAX_8U(p3, p4); CV_MINMAX_8U(p6, p7);
CV_MINMAX_8U(p1, p2); CV_MINMAX_8U(p4, p5);
CV_MINMAX_8U(p7, p8); CV_MINMAX_8U(p0, p3);
CV_MINMAX_8U(p5, p8); CV_MINMAX_8U(p4, p7);
CV_MINMAX_8U(p3, p6); CV_MINMAX_8U(p1, p4);
CV_MINMAX_8U(p2, p5); CV_MINMAX_8U(p4, p7);
CV_MINMAX_8U(p4, p2); CV_MINMAX_8U(p6, p4);
CV_MINMAX_8U(p4, p2);
dst[x] = (uchar)p4;
}
}
return CV_OK;
}
for( x = 0; x < size.width; x++, dst += cn )
{
uchar* dst_cur = dst;
uchar* src_top = src;
uchar* src_bottom = src;
int k, c;
int x0 = -1;
if( x <= m/2 )
nx++;
if( nx < m )
x0 = x < m/2 ? 0 : (nx-1)*cn;
// init accumulator
memset( zone0, 0, sizeof(zone0[0])*cn );
memset( zone1, 0, sizeof(zone1[0])*cn );
for( y = -m/2; y < m/2; y++ )
{
for( c = 0; c < cn; c++ )
{
if( x0 >= 0 )
UPDATE_ACC01( src_bottom[x0+c], c, += (m - nx) );
for( k = 0; k < nx*cn; k += cn )
UPDATE_ACC01( src_bottom[k+c], c, ++ );
}
if( (unsigned)y < (unsigned)(size.height-1) )
src_bottom += src_step;
}
for( y = 0; y < size.height; y++, dst_cur += dst_step )
{
if( cn == 1 )
{
for( k = 0; k < nx; k++ )
UPDATE_ACC01( src_bottom[k], 0, ++ );
}
else if( cn == 3 )
{
for( k = 0; k < nx*3; k += 3 )
{
UPDATE_ACC01( src_bottom[k], 0, ++ );
UPDATE_ACC01( src_bottom[k+1], 1, ++ );
UPDATE_ACC01( src_bottom[k+2], 2, ++ );
}
}
else
{
assert( cn == 4 );
for( k = 0; k < nx*4; k += 4 )
{
UPDATE_ACC01( src_bottom[k], 0, ++ );
UPDATE_ACC01( src_bottom[k+1], 1, ++ );
UPDATE_ACC01( src_bottom[k+2], 2, ++ );
UPDATE_ACC01( src_bottom[k+3], 3, ++ );
}
}
if( x0 >= 0 )
{
for( c = 0; c < cn; c++ )
UPDATE_ACC01( src_bottom[x0+c], c, += (m - nx) );
}
if( src_bottom + src_step < src_max )
src_bottom += src_step;
// find median
//重点介绍一下这部分代码
//计算过16级和256级的灰度直方图之后,查找中值就很简单了,相见论文“A Fast Two-Dimensional Median Filtering Algorithm”。
//这里看一下openCV的实现过程,论文中介绍了利用直方图进行中位数计算的方法,但是并未介绍使用16级的直方图,openCV编程的巧妙之处就在于他把两种直方图相
//结合,这样就会大大加速程序的执行效率。因为遍历一个16级的直方图很快,但是256级的直方图就会非常慢。openCV的这种思路还是值得大家学习的。
//至于里面的编程技巧,大家看着学吧!
for( c = 0; c < cn; c++ ){
int s = 0;
for( k = 0; ; k++ )
{
int t = s + zone0[c][k];
if( t > n2 ) break;
s = t;
}
for( k *= N; ;k++ )
{
s += zone1[c][k];
if( s > n2 ) break;
}
dst_cur[c] = (uchar)k;
}
if( cn == 1 )
{
for( k = 0; k < nx; k++ )
UPDATE_ACC01( src_top[k], 0, -- );
}
else if( cn == 3 )
{
for( k = 0; k < nx*3; k += 3 )
{
UPDATE_ACC01( src_top[k], 0, -- );
UPDATE_ACC01( src_top[k+1], 1, -- );
UPDATE_ACC01( src_top[k+2], 2, -- );
}
}
else
{
assert( cn == 4 );
for( k = 0; k < nx*4; k += 4 )
{
UPDATE_ACC01( src_top[k], 0, -- );
UPDATE_ACC01( src_top[k+1], 1, -- );
UPDATE_ACC01( src_top[k+2], 2, -- );
UPDATE_ACC01( src_top[k+3], 3, -- );
}
}
if( x0 >= 0 )
{
for( c = 0; c < cn; c++ )
UPDATE_ACC01( src_top[x0+c], c, -= (m - nx) );
}
if( y >= m/2 )
src_top += src_step;
}
if( x >= m/2 )
src += cn;
if( src + nx*cn > src_right ) nx--;
}
#undef N
#undef UPDATE_ACC
return CV_OK;
}
