多重共线性问题 -- 岭回归方法

概述

本篇博客分为两大部分，第一部分是最小二乘法作线性回归时会遭遇的问题：多重共线性问题。第二部分，使用岭回归解决第一部分中的多重共线性问题。

第一部分：线性回归最小二乘法的困境

第一部分借由1987-2007年的人口、消费和技术对碳排放的影响的数据来说明多重共线性问题（包括如何判断多重共线性问题）和多重共线性问题对普通最小二乘估计的影响。同时也给出线性模型定义和普通最小二乘法对线性模型的拟合的介绍

1.1 1987-2007年的人口、消费和科技对碳排放的影响

研究目的是量化分析人口、消费和技术因素对碳排放的影响，进而判断哪些因素是影响气候变化的主要因子。
文献[1]提出一个关于人文因素 （人口、经济和技术）对环境影响的量化模型STIRPAT模型：
$$I=\alpha P^b{A}^c{T}^{d}e\text{\hspace{1em}(1)}$$
其中，$\alpha$为模型系数，b、c、d为各自变量指数，e为误差。
对两边取自然对数，得到方程：
$$lnI=lna+b(lnP)+c(lnA)+d(lnT)+lne\text{\hspace{1em}(2)}$$
将人口城市化率引入模型，得到最终的扩展的STIRPAT模型：
$$lnI=lna+b_s(ln{P}_s)+b_c(ln{P}_c)+c(lnA)+d(lnT)+lne\text{\hspace{1em}(3)}$$

模型一般还会假设误差项$lne$满足正态分布、同方差，见附录1。
数据可以从这里下载链接：https://pan.baidu.com/s/1wl_TtsXLLSdZoT48U_fznw
提取码：2xeb
数据来源于文献[1]，如表1所示：

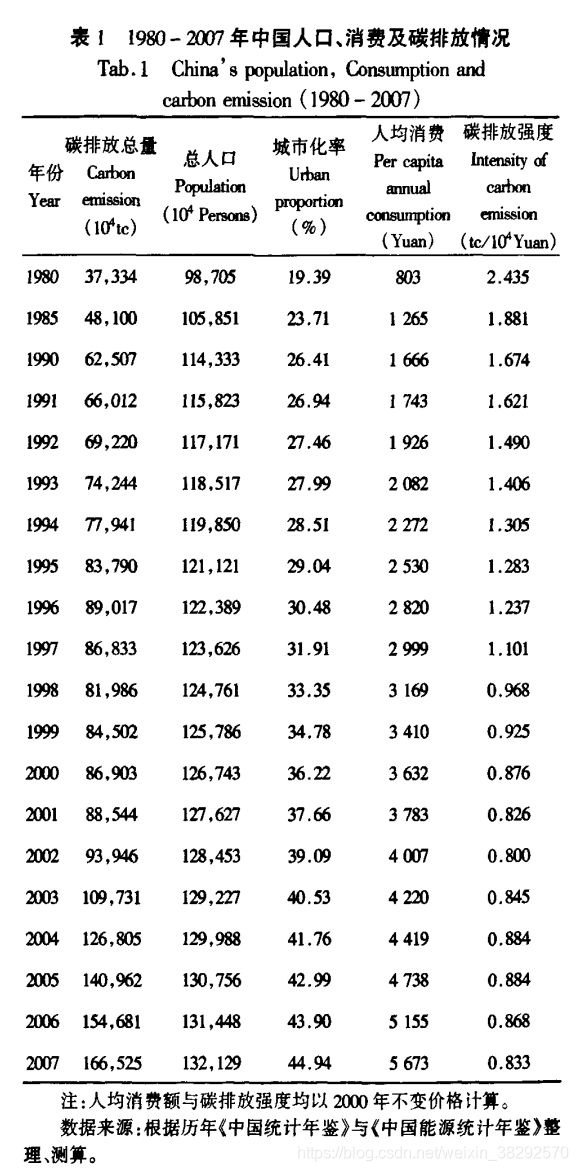
按照公式(3)，使用statsmodels库中的简单最小二乘法对公式（3）进行回归方程拟合。
statsmodels起源于Jonathan Taylor用R语言实现的各类统计分析模型，由Skipper Seabold 和Josef Perktold于2010年开始开发，实现各种统计模型和假设检验。
下面是数据读取和标准化代码：

import numpy as np
import pandas as pd
# 载入数据
file_path = "./PopulationConsumptionAndCarbonEmission1980_2007.csv"
data_df = pd.read_csv(open(file_path, encoding='utf-8'))
# 给列名重新命名，每一列就是一个自（因）变量的观测值
data_df.columns = ['year','I', 'Ps', 'Pc', 'A', 'T']
# 量纲恢复
data_df['I'] = data_df['I']*1e4
data_df['Ps'] = data_df['Ps']*1e4
data_df['T'] = data_df['T']*1e4
# 数据标准化
def Normalize(data):
    """对因变量作标准化变换,标准化因子选择是标准差，这个和文献[1]不相同"""
    return (data - data.mean())/data.std()

下面是statsmodels库中的简单最小二乘法拟合公式（3）的代码：

import statsmodels.api as sm
# 为了时间连续性，选取1990-2007年数据，下同。
X = np.log(data_df.iloc[2:,2:])
y = np.log(data_df.iloc[2:,1])
X = sm.add_constant(X)
ols_model = sm.OLS(y, X).fit()
print(ols_model.summary())

回归结果如下图所示：

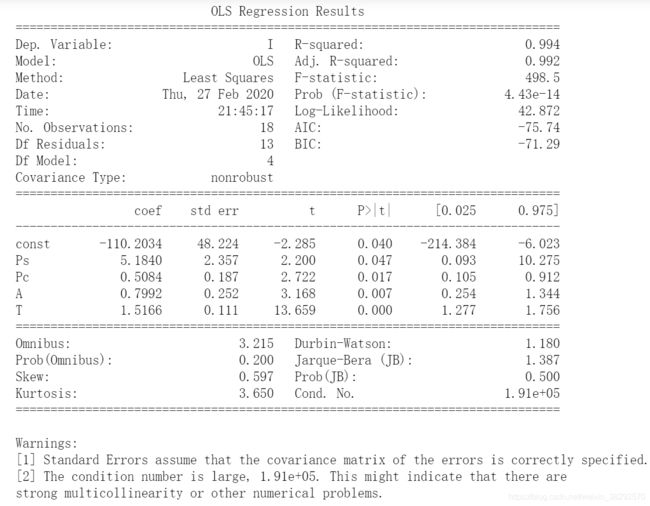
第二条警告说的是条件数太大，这可能表明存在强烈的多重共线性或其它数值问题。多重共线性指的是自变量之间存在线性相关关系，这个与线性回归的基本假设第一条“自变量之间互不影响”相违背（线性回归的基本假设见附录1），因此，此数据不满足线性回归的基本假设，自然不可以使用简单线性回归进行公式(3)的拟合。最终解决办法放在第二部分介绍，下面深入介绍自变量之间的多重共线性问题如何判断。

1.2 数据多重共线性的判断

本小节参考自文献[3]，通过三种方法来判断：相关系数（粗略判断有无）、方差扩大因子法（variance inflation factor, VIF）和条件数法。

下面的数据标准化操作是为了消除量纲不同和不同数量级的差异所带来的的影响，见文献[1]的P76。

1.3.1 相关系数计算

# 为了时间连续性，选取1990-2007年数据，下同。
rxy = np.log(data_df.iloc[2:,1:]).corr(method='pearson')

rxy的结果如下图所示：

可见，任意两个自变量之间的相关系数的绝对值都超过了0.5，说明两两自变量之间的线性关系很明显[3]。

1.3.1 方差扩大因子法

def VIF_value(normal_x):
    """计算方差扩大因子VIF
       输入：标准化的自变量观测值,normal_x
       返回：每个自变量的VIF值
    """
    # 计算自变量之间的两两相关系数
    rxx = normal_x.corr(method='pearson')
    # 计算相关系数矩阵的逆
    C = np.matrix(rxx).I 
    # 返回方差扩大因子，C对角线上元素，并保留两位小数
    return np.diag(C).round(2)
# 计算1990-2007年数据中自变量的方差扩大因子
X = np.log(data_df.iloc[2:,2:])
y = np.log(data_df.iloc[2:,1])
vif = VIF_value(Normalize(X))

计算结果是：array([282.92, 29.2 , 221.86, 19.76])。当自变量$x_i$方差因子大于10，说明自变量$x_i$与其余自变量存在共线性。显然这里每一个自变量都与其余自变量存在线性关系[3]。

1.3.1 条件数法

def Condition_number(normal_x):
    """
    返回条件数、特征值和特征向量
    输入:标准化后的自变量观测值；
    返回:条件数、特征值和特征向量
    """
    x_array = np.array(normal_x)
    # 计算x_array的特征值和特征向量
    ev, evct = np.linalg.eig(np.dot(x_array.T,x_array))
    # 计算条件数
    k = ev.max()/ev.min()
    return k, ev, evct
# 计算1990-2007年数据中自变量的条件数
X = np.log(data_df.iloc[2:,2:])
y = np.log(data_df.iloc[2:,1])
k,_,_ = Condition_number(Normalize(X))

条件数计算结果是k = 1912.8255998684424。
条件数检验准则是[3]：

• 若 $100\le k\le 1000$，则认为存在较强的多重共线性；
• 若$1000\le k$,则认为存在严重的多重共线性。
  由k= 1912.8可知，自变量之间存在严重的多重共线性。但是，这个地方我有个疑问，为什么这里计算的条件数和上面statsmodels中计算的不一样？虽然这个不影响对多重共线性问题结果的判断。

第二部分 多重共线性的消除与岭回归

现在开始解决第一部分中的自变量之间多重共线性问题，文献[1]并不想通过剔除共线性自变量来解决问题，因为文献[1]想要研究这四个自变量对因变量的影响显著程度。因此，岭回归便成了唯一的办法。

岭回归的核心思想是：既然共线性会使得回归参数估值过大，那么就回归参数加入惩罚项，来控制回归参数的估计范围，从而弱化共线性对回归参数估计的影响。

研究了好久 statsmodels的官网https://www.statsmodels.org/stable/index.html，而且这个网站响应太慢了，网页刷新一次要好久，也没有找到岭回归方法，也不知道是不是没有这个，希望有知道的小伙伴能在评论区交流交流。

2.1 sklearn岭回归

于是，我就使用了sklearn中的岭回归，解决这个多重共线性问题。代码如下：

# 载入标准化后的数据
X, y = Normalize(data_df.iloc[2:,2:]), Normalize(data_df.iloc[2:,1])
# 指定alpha系数范围
k = np.linspace(0.2,1,20)
ridge_reg = linear_model.RidgeCV(alphas=k)
# 用数据拟合模型
ridge_reg.fit(X, y)
print(ridge_reg.coef_,ridge_reg.alpha_,,ridge_reg.intercept_)

最终结果，岭回归系数是 [0.62645745, 0.01831523, 1.0759906 , 0.89142276]，$\alpha =0.2$,常数项intercept_约等于0,sklearn中没有对回归系数进行显著性检验的工具（对于为什么是这样文献[3]给出了说明，整理在了本文附录2中），只有对回归方程显著性检验指标$R^2$决定系数，代码如下。

ridge_reg.score(X,y)

结果为0.9768888111923794。还算能够接受。于是，拟合得到如下标准化岭回归方程（即通过标准化自变量观测数据拟合的回归方程）。
$$ln\hat{I}=0.6265(ln{\hat{P}}_s)+0.0183(ln{\hat{P}}_c)+1.0760(ln\hat{A})+0.8914(ln\hat{T})\text{\hspace{1em}(4)}$$
按照下面代码计算得到（非标准化的）岭回归方程：

X = np.log(data_df.iloc[2:,2:])
y = np.log(data_df.iloc[2:,1])
# 计算非标准化的岭回归方程系数
coef_ = ridge_reg.coef_*(y.std()/X.std())

$$lnI=3.9323(ln{P}_s)+0.0284(ln{P}_c)+0.8165(lnA)+0.9975(lnT)\text{\hspace{1em}(5)}$$

2.2 计算结果分析

首先要说的是，本文结果 和原文文献[2]有较大出入，如有不合理之处，欢迎大家在评论区交流。

按照公式 （4），我国1990-2007该阶段碳排放的解释因素按其影响比重大小，依次是：人均消费（1.0760）、碳排放强度（0.8914）、人口数量（0.6265）和城市化率（0.0183）。

文献[2]中的次序是：人均消费（0.3454）、城市化率（0.3414）、人口数量（0.2970）、碳排放强度（0.0374）

同样的就是文献[1]在人均消费这个因素上没有将物价通货膨胀的影响纳入考虑，如果考虑进去后，碳排放强度可能会抢占第一。人均消费第一 说明，该阶段财富增长刺激了人们消费的欲望，而消费增长将会对碳排放产生直接的促进作用。即居民消费水平的提高对碳排放产生了深刻的影响。

碳排放强度指的是万元GDP碳排放的量。该阶段我国大力发展房地产经济和劳动密集型产业，房地产经济带动的水泥石化等碳排放很大的重工业 ，该阶段北京等地区春秋季多雾霾现象也从另一方面印证碳排放强度这个因素对该阶段碳排放的影响（雾霾成因多种多样，有自然客观因素，也有人类活动因素，其中人类活动主要表现在：汽车尾气、工业排放、建筑扬尘、垃圾焚烧等）。这个反映出我国在发展中的工业化进程对碳排放有着重大影响，也符合西方国家的工业化历史发展，所以说碳排放强度因素对该阶段碳排放影响占重要地位也符合工业化历史规律。

值得注意的是，碳排放强度高于人口数量和城市化率，这说明我国进行节能减排和发展绿色经济对于减少碳排放将会有显著的成效。

人口数量和碳排放强度差距并不是特别多，这也说明人口规模依然是我国资源和环境压力的主要因素之一。

附录1:线性模型和普通最小二乘法

线性模型是指预测值是特征（feature）的线性组合（liner combination），数学表达式如下：
$$\widehat{y_i}={\beta }_0+{\beta }_1{x}_{i1}+...+{\beta }_p{x}_{ip}\text{\hspace{1em}(4)}$$
$$y_i={\hat{y}}_i+{ϵ}_i\text{\hspace{1em}(5)}$$
$i=1,2,...,n$
其中：
$\hat{y}$是预测值（也叫因变量）；
$y$是真实值；
$\beta =({\beta }_1,...,{\beta }_p)$是系数coef_;
${\beta }_0$是截距intercept_;
$x_{i1},...,x_{ip}$是第$i$个样本点, 是$x$的行向量;
${ϵ}_i$是第$i$个样本点估计的误差项。

普通最小二乘法拟合线性模型，本质上解决的是：
$$\underset{\beta }{\min }||x\beta -y|{|}_2^2$$
其中：
$\beta =({\beta }_1,...,{\beta }_p)$是回归系数coef_;
$x=(x_1,...,x_p)$是$x$的列向量，也叫自变量;
$y=(y_1,y_2,...,y_p)$是样本观测值（也叫自变量）;

线性回归模型基本假设：

• 自变量$x_1,x_2,..,x_p$是确定的观测值，且互不影响。
• 因变量与自变量之间是近似线性的关系，即公式（4）所示；
• 误差项${ϵ}_i$的均值为0，方差形同，且两两不相关。

$$\{\begin{array}{rlr}E({ϵ}_i)& =& 0\\ var({ϵ}_i)& =& {\sigma }^2\\ cov({ϵ}_i,{ϵ}_j)& =& 0\end{array}$$
其中，$$i\ne j,i=1,2,...,n;j=1,2,...,n$$

也就是说如果自变量$x_i$与$x_j$的相关时，最小二乘法的估计值会对自变量X中的随机误差极其敏感，会产生很大的方差。在没有实验设计就进行数据收集，很容易在自变量之间产生多重共线问题。

附录 2：回归模型和其在经典统计学 、机器学习中应用

F2.1 回归模型

• 回归的意思是趋向平均
• 回归的模型有线性模型和非线性（逻辑回归）之分

F2.2 统计学中回归分析

• 回归方程系数${\beta }_0,{\beta }_1$等的估计方法;
• 估计量${\hat{\beta }}_0,{\hat{\beta }}_1$的统计性质：无偏性和有效性;
• 统计性质检验：t检验、F检验
• 模型假设诊断：误差项是否满足独立、同方差的假设等
• 新样本点输出值的预测

F2.3 机器学习中的回归分析

• 以算法为中心进行处理数据
• 假设数据背后的理论结构是复杂和未知的：因而不太关注模型的假设和统计检验
• 致力于用算法模拟数据产生的过程，从而达到较好的预测效果
• 缺陷是理论可解释性差

F2.4 统计学视角和机器学习视角对比

• 统计学视角是以数学模型为基础，基于人类既有的经验和理论推导，需要对问题场景和数据特征做出种种假设（例如误差项服从正态分布等）
• 大数据时代，数据越来越复杂，无法满足统计视角下的种种假设，或者是已经超出了人类既有的经验和理论。机器学习提供了一个从数据本身的角度探寻的可能。
• 适当的做法是结合统计学和机器学习，进行适当的综合（具体怎么做没想法，目前只有这个概念）

参考文献

[1]何晓群,刘文卿.应用回归分析(第三版)[M].中国人民大学出版社
[2]朱勤, 彭希哲, 陆志明, et al. 人口与消费对碳排放影响的分析模型与实证[J]. 中国人口.资源与环境, 2010(02):102-106.
[3]https://www.bilibili.com/video/av80412525?p=27
[4]https://zhuanlan.zhihu.com/p/72722146