MATLAB07:数值计算
目录
多项式的数值运算
使用MATLAB表示多项式
使用向量表示多项式
多项式求值:polyval()
多项式的乘法:conv()
多项式的数值运算
多项式的因式分解:roots()
多项式的微分:polyder()
多项式的积分:polyint()
非线性表达式的数值运算
方程(组)求根fsolve()
数值微分
求差分:diff()
求导数:diff(y)./diff(x)
数值积分
数值积分原理
数值积分函数:integral()
学习一门技术最好的方式就是阅读官方文档,可以查看MATLAB官方文档
多项式的数值运算
使用MATLAB表示多项式
使用向量表示多项式
在MATLAB中,多项式可以用向量表示,向量中的元素为多项式的系数(降幂排序):第一位为多项式最高次项系数,最后一位为常数项.
例如多项式:
![]()
可以用向量p = [1 0 -2 -5]表示.
多项式求值:polyval()
使用polyval(p, x)可以计算多项式p在x的每个点处的值.
a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f);
多项式的乘法:conv()
使用conv(p1, p2)函数可以对两个向量p1和p2进行卷积相乘,用于计算多项式的乘法.
例如多项式:
![]()
可以使用conv()函数得到展开后的多项式:
p = conv([1 0 1], [2 7])
得到p = [2 7 2 7].
多项式的数值运算
多项式的因式分解:roots()
使用roots(p)函数可以对多项式p进行因式分解,即求表达式值为0的根.
p = roots([1 -3.5 2.75 2.125 -3.875 1.25])
得到p = [2 -1, 1+0.5i, 1-0.5i, 0.5],表示
多项式的微分:polyder()
使用polyder(p)函数可以计算多项式的导数.
例如对下面多项式求导:
![]()
p = polyder([5 0 -2 0 1]);
得到p = [20 0 -4 0],表示计算得到导数![]()
多项式的积分:polyint()
使用polyint(p, k)函数可以计算多项式p的积分,积分结果的常数项设为k.
例如对下面多项式求导:
![]()
p = polyint([5 0 -2 0 1], 3)
得到p = [1 0 -0.6667 0 1 3],表示计算得到积分
非线性表达式的数值运算
方程(组)求根fsolve()
使用fsolve(fun, x0)求非线性方程组的根,fun为待求方程的函数句柄,x0为初值.
-
求方程
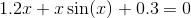 在
在 附近的解.
附近的解.f2 = @(x) (1.2*x+x*sin(x)+0.3); fsolve(f2,0) % 得到 -0.3500 -
解方程组
设定初值为[0,0]
fun = @(x) [exp(-exp(-(x(1)+x(2))))-x(2)*(1+x(1)^2)...
x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5]
x0 = [0,0];
x = fsolve(fun,x0) % 得到[0.3532 0.6061]
数值微分
求差分:diff()
使用diff(X, n)计算向量X的n阶差分,n默认为1.
x = [1 2 5 2 1];
diff(x); % 得到 [1 3 -3 1]
diff(x,1); % 得到 [1 3 -3 1]
diff(x,2); % 得到 [2 -6 2]
求导数:diff(y)./diff(x)
使用导数的定义
可以计算函数在某点的近似导数.
x0 = pi/2; h = 0.1;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x) % 得到 m = -0.005
h的取值越小,得到的近似导数越精确.
下面程序计算![]() 的一阶和二阶导数的值.
的一阶和二阶导数的值.
x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x); % 计算一阶导数
m2 = diff(m)./diff(x(1:end-1)); % 计算二阶导数
plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x'); ylabel('y');
legend('f(x) =x^3','f''(x)','f''''(x)', 4);
数值积分
数值积分原理
有三种常见算法用于计算数值积分: 矩形法,梯形法,抛物线法,它们分别把微分区间的图形视为矩形,梯形,抛物线以计算面积.
| 算法 | 图示 | 表达式 |
|---|---|---|
| 矩形法(Midpoint Rule) |  |
 |
| 梯形法(Trapezoid Rule) |  |
![\int_a^b f(x) dx = \frac{h}{2} \left[ f(a) + 2\sum_{i=1}^{n-1} f(x_i) +f(b) \right]](http://img.e-com-net.com/image/info8/8adeea0ffeb34b62ae1dc7373e45c12a.gif) |
| 抛物线法(Simpson’s Rule) |  |
![\int_a^b f(x) dx = \frac{h}{3} \left[ f(a) + 2\sum_{i=1}^{(n/2)-1} f(x_{2i}) + 4\sum_{i=1}^{n/2} f(x_{2i-1}) + f(b) \right]](http://img.e-com-net.com/image/info8/9de08ec31b894580987f605ec015cc76.gif) |
下面分别使用三种方法计算![]() 在区间(0,2)内的积分.
在区间(0,2)内的积分.
h = 0.05; x = 0:h:2;
y = 4*midpoint.^3;
% 使用矩形法计算近似积分
midpoint = (x(1:end-1)+x(2:end))./2;
s = sum(h*y) % 得到 15.9950
% 使用梯形法计算近似积分
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid) % 得到 15.2246
% 使用抛物线法计算数值积分
s = h/3*(y(1)+2*sum(y(3:2:end-2))+4*sum(y(2:2:end))+y(end)) % 得到 15.8240
数值积分函数:integral()
integral(),integral2(),integral3()分别对函数在xmin至xmax间进行一重,二重,三重积分.
它们的第一个参数都应该是一个函数句柄,下面例子演示他们的用法:




