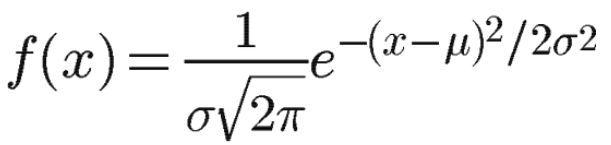【图像处理基础知识】-混合高斯背景建模
0、高斯模糊原理
转载地址:https://www.cnblogs.com/herenzhiming/articles/5276106.html
-------------------------------------------------------分割线----------------------------------------------------------------
1、一维高斯函数:
![]()
a表示得到曲线的高度,b是指曲线在x轴的中心,c指width(与半峰全宽有关),图形如下:
![]()
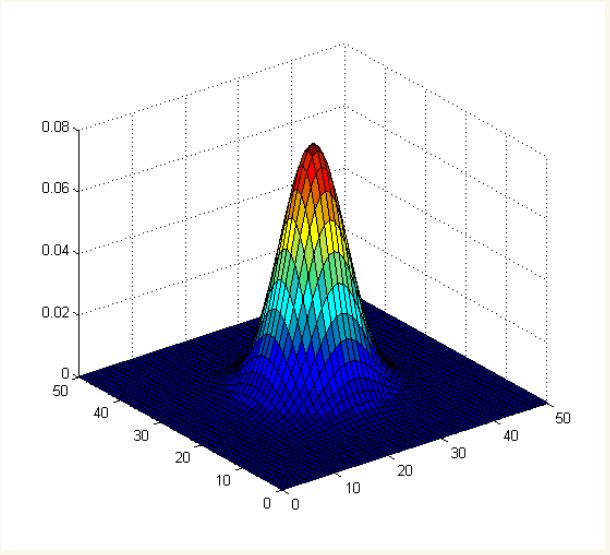
2、根据一维高斯函数,可以推导得到二维高斯函数:
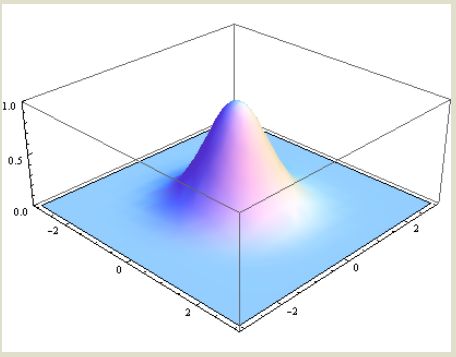
在图形上,正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。例如:通常,图像处理软件会提供"模糊"(blur)滤镜,使图片产生模糊的效果。
"高斯模糊"(Gaussian Blur)。它将正态分布(又名"高斯分布")用于图像处理。
数据平滑技术(data smoothing),适用于多个场合,图像处理恰好提供了一个直观的应用实例。
高斯模糊的原理
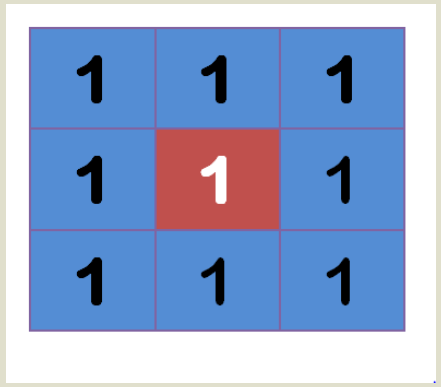
所谓"模糊",可以理解成每一个像素都取周边像素的平均值。
上图中,2是中间点,周边点都是1。
"中间点"取"周围点"的平均值,就会变成1。在数值上,这是一种"平滑化"。在图形上,就相当于产生"模糊"效果,"中间点"失去细节。
显然,计算平均值时,取值范围越大,"模糊效果"越强烈。
上面分别是原图、模糊半径3像素、模糊半径10像素的效果。模糊半径越大,图像就越模糊。从数值角度看,就是数值越平滑。
接下来的问题就是,既然每个点都要取周边像素的平均值,那么应该如何分配权重呢?
如果使用简单平均,显然不是很合理,因为图像都是连续的,越靠近的点关系越密切,越远离的点关系越疏远。因此,加权平均更合理,距离越近的点权重越大,距离越远的点权重越小。
正态分布的权重
正态分布显然是一种可取的权重分配模式。
在图形上,正态分布是一种钟形曲线,越接近中心,取值越大,越远离中心,取值越小。
计算平均值的时候,我们只需要将"中心点"作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权平均值。
高斯函数
上面的正态分布是一维的,图像都是二维的,所以我们需要二维的正态分布。
"高斯函数"(Gaussian function)。它的一维形式是
其中,μ是x的均值,σ是x的方差。因为计算平均值的时候,中心点就是原点,所以μ等于0。
根据一维高斯函数,可以推导得到二维高斯函数
有了这个函数 ,就可以计算每个点的权重了。
权重矩阵
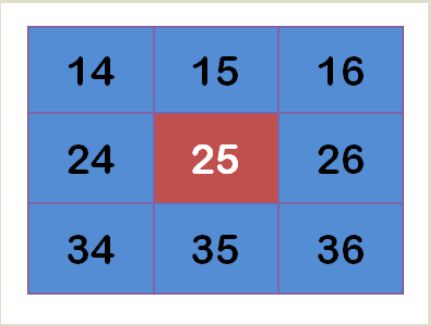
假定中心点的坐标是(0,0),那么距离它最近的8个点的坐标如下:
更远的点以此类推。
为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:
这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。
计算高斯模糊
有了权重矩阵,就可以计算高斯模糊的值了。
假设现有9个像素点,灰度值(0-255)如下:
每个点乘以自己的权重值:
得到
将这9个值加起来,就是中心点的高斯模糊的值。
对所有点重复这个过程,就得到了高斯模糊后的图像。如果原图是彩色图片,可以对RGB三个通道分别做高斯模糊。
二、高斯(核)函数简介
1函数的基本概念
所谓径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 , 可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/2*σ^2) } 其中xc为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。
高斯函数具有五个重要的性质,这些性质使得它在早期图像处理中特别有用.这些性质表明,高斯平滑滤波器无论在空间域还是在频率域都是十分有效的低通滤波器,且在实际图像处理中得到了工程人员的有效使用.高斯函数具有五个十分重要的性质,它们是:
(1)二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的.一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向.
(2)高斯函数是单值函数.这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的.这一性 质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真.
(3)高斯函数的付立叶变换频谱是单瓣的.正如下面所示,这一性质是高斯函数付立叶变换等于高斯函数本身这一事实的直接推论.图像常被不希望的高频信号所 污染(噪声和细纹理).而所希望的图像特征(如边缘),既含有低频分量,又含有高频分量.高斯函数付立叶变换的单瓣意味着平滑图像不会被不需要的高频信号 所污染,同时保留了大部分所需信号.
(4)高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的.σ越大,高斯滤波器的频带就越宽,平滑程度就越好.通过 调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷.
(5)由于高斯函数的可分离性,大高斯滤波器可以得以有效地实现.二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同一维高斯函数卷积.因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长.
参考:
http://www.ruanyifeng.com/blog/2012/11/gaussian_blur.html
http://www.cnblogs.com/pzxbc/archive/2012/02/14/2351708.html
http://baike.baidu.com/view/1097446.htm?fr=aladdin
1、混合高斯背景建模原理
转载地址:https://www.cnblogs.com/wangjunqun/p/3337840.html
---------------------------------------------------------分割线--------------------------------------------------------
目前,基于二值化图像提取运动目标仍具有广泛的应用。但是,在提取运动目标之前必须进行背景建模。
背景建模的方法很多,如平均法,最大值最小值统计法,单高斯建模法,加权平均法等,而混合高斯背景建模应该来说是比较成功的一种。
为什么这么说呢? 机器视觉算法提取运动目标面临的基本问题:图像抖动,噪声干扰,光线变化,云飘动,阴影(包括目标阴影和区域外物体阴影),区域内部反光(如水面,显示器),运动目标缓慢移动等。那我们来看看,混合高斯背景建模是怎么解决这些问题的?从混合高斯模型的原理一看便知。
混合高斯模型的原理
图像中每个像素点的值(或特征)短时间内都是围绕与某一中心值一定距离内分布,通常,中心值可以用均值来代替,距离呢可以用方差来代替。这种分布呢是有规律的,根据统计定律,如果数据点足够多的话,是可以说这些点呈正态分布,也称为高斯分布(取名高斯,大概是因为很多地方都用这个名字吧)。根据这个特点,如果像素点的值偏离中心值较远,那么,这个像素值属于前景,如果像素点的值偏离中心值很近(在一定方差范围内),那么可以说这个点属于背景。理论上,如果不存在任何干扰的话,是可以准确区分前景和背景的。但是,现实往往不尽如人意,如果画面中光线变化的话,这个高斯分布的中心位置是会改变的。如果光线强度改变的话,在原来那个位置并没有无数个点供统计,因此,不符合大数定理,也就不能说那个点的分布满足正态分布了,只能说是近似为高斯分布。
混合高斯模型指这个像素点值存在多个中心位置,如来回摆动的树叶,波光粼粼的水面,闪烁的显示器,图像中特征边缘位置的抖动等,这些都会引起某个像素点会在多个中心位置聚集大量的点,每个位置便会产生一个高斯分布,四个以上的高斯分布其实并不常见,这便是混合高斯模型的由来。混合高斯背景建模主要用来解决背景像素点具有多峰特性的场合,如在智能交通场景中,解决视频画面抖动带来的干扰。
针对光线变化的问题,混合高斯模型通过比较当前像素点的值与高斯分布中心位置,选择一定的加权系数对当前高斯分布的中心位置进行更新,以便于适应缓慢的光线变化。言外之意,高斯分布并不能解决光线的突变问题,如云飘动,阴影。个人认为,阴影或云飘动并不属于背景建模的内容。
此外,混合高斯模型尤其适合于检测缓慢移动的物体,因为背景已是一个高斯分布,如果车停下来,等到聚集一定的前景数据便会形成一个新的高斯分布,停下来的车也会便是背景。但是如果车缓慢行驶的话,是很难在短时间内形成一个新的高斯分布,也就是应用混合高斯分布很容易检测缓慢行驶的车辆。
混合高斯背景建模的优点
图像画面中,其实每个像素(也可以说是局部单元),其运动变化特性是不一样的,这才是混合高斯模型具有优势的主要原因。普通的二值化目标分割,整个画面采用同一阈值,无论这个阈值是固定的,还是自适应的,都存在本质性的缺陷,属于有缺陷的分割,这种算法带有不稳定性,无论怎么调整分割参数,也解决不了根本性的问题。因为,画面中每个部分,其实分割阈值是不一样的。一定得建立统计学的方法,进行局部分割,而混合高斯模型正是采用局部分割的一种算法。
混合高斯背景建模方法评价
从理论上来说,混合高斯背景建模真是一种较为完美的背景分割方法。但是由于像素值在光线干扰下在中心位置停留时间较短,围绕这一中心位置波动的数据准确地来说并不属于高斯分布,因此也就无法准确地确定这些数据的中心值及方差,造成实际分割的效果并不完美。
以上阐述属于个人看法,仅作参考,希望今后能对分割问题理解更深刻,欢迎与大家交流,共同学习!