数据结构学习笔记04----链表与线性表
目录
一、链表
1.单向链表
1）单向链表节点的定义
2）节点空间申请
3）何为单链表
4）求单链表的长度
5）找链表中第k个元素的值
5）链表的插入操作
6）带头节点的链表
7）单链表的逆转
8）求单链表中所有节点Data的阶乘和
二、线性表
1.线性结构的含义以及表示方式
2.结构的实现（数组）
3.基本函数
1）寻找线性表中元素X的下标。
2）线性表达插入操作
3）线性表达删除操作
一、链表
链表是将若干个元素通过指针的方式链接起来的一种结构。
1.单向链表
1）单向链表节点的定义
typedef是给一个类型定义一个别名，目的是简化变量的定义，比如：
int * pp;//p是一个整型的指针，但是这样定义比较繁琐，C语言提供一个关键字typedef，其用法可以表示为：
typedef int* p;//声明了一个类型别名，此别名为p，它表示一个整型的指针，p是一个类型名
p p1,p2//p1和p2是指针变量，这是变量定义由此单向链表节点我们可以定义为：
typedef struct Node *PtrToNode;
struct Node {
ElementType Data; /* 存储结点数据 */
PtrToNode Next; /* 指向下一个结点的指针 */
}; 因此
是一个指针，指向
类型，等价于
。所以上面的一个节点有两个元素，一个时存放数据的
，
表示一个指针，指向此结构类型。
2）节点空间申请
//分配大小为sizeof（Node）的一段内存，单位为字节，并将这段内存设置成PtrToNode类型
PtrToNode p = (PtrToNode)malloc(sizeof(struct Node));
3）何为单链表
typedef PtrToNode List; /* 定义单链表类型 */ 由此我们看出，节点的类型和链表的类型时一个类型，都是
，为何还要区分？当指向首元素时的节点用链表，普通节点用。
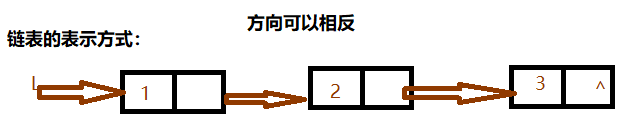
我们建立一个结构，结构又两个成员，其中一个是数据，另一个是指针，用来指向后续的元素。
假设有单链表L如图所示，L实际是个指针，可以用该指针访问该链表的成员。即: 
,
,
代码实现单链表：
SingleList::SingleList(int Data[], int len)
{
m_pNode = (PtrToNode)new char[sizeof(Node)];
m_pNode->Data = Data[0];
m_pNode->Next = NULL;
PtrToNode temp = m_pNode,newPnode;
for (int i = 1; i < len; i++) {
newPnode = (PtrToNode)new char[sizeof(Node)];
newPnode->Data = Data[i];
newPnode->Next = NULL;
temp->Next = newPnode;
temp = newPnode;
}
}
4）求单链表的长度
问题的核心是用一个指针变量遍历单链表。
int SingleList::Length()
{
int cnt = 0;/*初始化计数器*/
PtrToNode p = this->m_pNode;/*p指向表的第一个结点*/
while (p) {
p = p->Next;
cnt++;/*当前p指向的是第cnt个结点*/
}
return cnt;
}5）找链表中第k个元素的值
int SingleList::FindKth(int K)
{
/*根据指定的位序K，返回L中相应元素*/
int cnt = 1;/*位序从1开始*/
PtrToNode p = this->m_pNode;/*p指向L的第1个结点*/
while (p && cntNext;
cnt++;
}
if ((cnt == K) && p)
return p->Data;/*找到第K个*/
else
return ERROR;/*否则返回错误信息*/
} 问题①：为何cnt初始化为1？cnt = 1要与p=m_pNode（链表首节点），因为你的目的是找第几个元素。
②：while结束时，cnt==？ 若正常结束，则cnt == k，指没有提前退出。如果cnt = k，并且p也是空，此时p有问题，它不能访问Data。
【notice】：链式存储的结构定义的ERROR是NULL，而顺序存储的结构ERROR定义为-1.
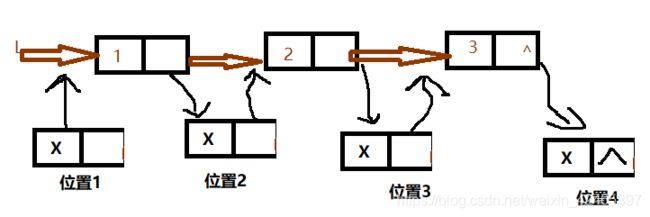
5）链表的插入操作
问题①：插入元素的位置：加入有链表有三个元素，那么插入元素的位置可以是1,2,3,4。1,2,3,4的意思是插入元素插入完后在单链表中的次序。
问题②：当在第i个位置插入
元素时，需要前一个节点的指针pre。
代码分析：
void SingleList::Insert(int X, int i)
{
PtrToNode tmp, pre;
tmp = (PtrToNode)new char[sizeof(Node)];/*申请、填装结点*/
tmp->Data = X;
if (i == 1) {/*新结点插入在表头*/
tmp->Next = m_pNode;
m_pNode = tmp;/**更新链表头节点*/
}
else {
/*查找位序为i-1的结点*/
int cnt = 1;/*位序从1开始*/
pre = m_pNode;/*pre指向L的第1个结点*/
while (pre&&cntNext;
cnt++;
}
if (pre == NULL || cnt != i - 1) {/*所找结点不在L中*/
cout<<"插入位置参数错误\n"<Next = pre->Next;
pre->Next = tmp;
}
}
} 参数X表示插入元素，i表示插入位置。
如果位置为1，即i == 1，那就直接令新插入节点的next为原链表头节点，并更新链表头节点。
当i ！= 1时，需要i-1的位置，于是就有用循环找第i-1个元素。
6）带头节点的链表
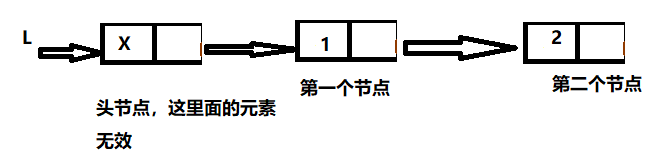当对其进行插入操作时，只需要在上面的程序中将cnt = 1改成cnt = 0即可。
下面我们看带头节点的单链表的删除操作：
程序返回值是bool，因为带头节点，只需要判断是否插入成功即可。
bool SingleList::Delete(int i)
{
PtrToNode tmp, pre;
int cnt = 0;
/*查找位序为i-1的结点*/
pre = m_pNode;/*pre指向表头*/
while (pre&&cntNext;
cnt++;
}
if (pre == NULL || cnt != i - 1 || pre->Next == NULL) {
/*所找结点或位序为i的结点不在L中*/
cout<<"插入位置参数错误\n"<Next;
pre->Next = tmp->Next;
free(tmp);
return true;
}
} 为啥设置头节点？当带头节点时，对其操作后链表L不变，当不带头节点时，(尤其是对首节点做操作时)L可能会变，所以加上头节点会简化操作。
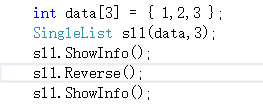
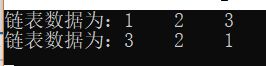
7）单链表的逆转
链表的逆转可以表示为:
怎么做？我们把元素都取出来然后再放入新的链表中，放入时由于我们这是单链表，先取到的是第一个，但是先取到的我们要后放，所以关键问题是如何把后取到的元素插入到先取到的元素前（即如何倒叙插入元素）。
void SingleList::Reverse()
{
PtrToNode Old_head, New_head, Temp;//分别为旧的头节点，新的头节点，临时变量Temp
//让Old_head指向链表，便于一个一个的取出元素，所以Old_head是待处理元素
Old_head = this->m_pNode; /* 初始化当前旧表头为当前链表的节点 */
New_head = NULL; /* 初始化逆转后新表头为空，这样既保证了第一个节点指向空，又保证后续节点都反向插入 */
while (Old_head) { /* 当旧表不为空时，当为空时链表就结束了 */
Temp = Old_head->Next;//保存头节点给下次循环用
Old_head->Next = New_head;//倒叙插入，把旧链表节点插入到新链表中去，所以整个插入过程就是就链表头节点不停后移，新链表头节点不停更新的过程
New_head = Old_head; /* 将当前旧表头逆转为新表头 */
Old_head = Temp; /* 为下次运行更新旧表头 */
}
this->m_pNode = New_head; /* 更新L */
}调用及运行结果：
8）求单链表中所有节点Data的阶乘和
这个问题较简单，关键是遍历一个链表：step1：定义一个指针指向链表首元素；
step2：用while（p）依次访问每个元素
int SingleList::FactorialSum()
{
/* 求单链表L中所有结点Data的阶乘和 */
/* 这里默认所有结点的Data值非负 */
int Fact, Sum, i;
PtrToNode P = this->m_pNode;//将首节点赋给P
Sum = 0;
while (P) {
Fact = 1;
for (i = 2; i <= P->Data; i++)
Fact *= i;
Sum += Fact;
P = P->Next;
}
return Sum;
}
二、线性表
1.线性结构的含义以及表示方式
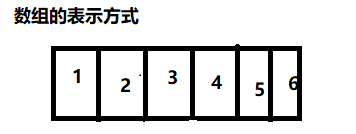
线性表就是线性表示的意思，一种是顺序表示，一种是链表的表示。线性结构就是从前向后（从后向前）的单一的结构方式，有两种表示方式，即：
2.结构的实现（数组）
既然是用数组描述，那么我们必须知道数组的的描述方式，一种是用数组的长度，另一种是用最后一个元素下标描述。
定义一个结构体LNode，其有两个成员，一个是由MAXSIZE大小的数据数组，另一个是该数组的最后一个元素的下标。
typedef int Position;
typedef struct LNode* PtrToLNode;
struct LNode {
int Data[MAXSIZE];
Position Last;
};
typedef PtrToLNode List;
class LArray
{
public:
LArray(int a[],int len);
friend ostream & operator <<(ostream & out, const LArray ptrla);
~LArray();
private:
List L;
};其构造函数可以为：
LArray::LArray(int a[],int len)
{
L = (List)new char[(sizeof(LNode))];
L->Last = -1;//这是最后一个元素的下标
if (len < 10) {
memcpy(L->Data, a, len*sizeof(int));
L->Last = len - 1;
}
else {
memcpy(L->Data, a, MAXSIZE * sizeof(int));
L->Last = MAXSIZE - 1;
}
}3.基本函数
1）寻找线性表中元素X的下标。
问题的关键：遍历线性表并进行寻找元素X。由于是数组方式存储的数据，所以用![data[i]](http://img.e-com-net.com/image/info8/1f323c971a7d4c5b9f1e54c072adb58f.gif){kind=small}
取遍历
Position LArray::Find(int X)
{
Position i = 0;
while (i <= L->Last&&L->Data[i] != X)//遍历线性表
i++;
if (i>L->Last)return ERROR;/*如果没找到，返回错误信息，ERROR是个宏定义，为-1*/
else return i;/*找到后返回的是存储位置*/
}2）线性表达插入操作
类似于向数组中的插入元素。【注】：Last是数组中最后一个元素的下标，而传入的i是指你要在哪个位置插入，从1开始。
bool LArray::Insert(int X, int i)
{
/*在L的指定位序i前插入一个新元素X;位序i元素的数组位置下标是i-1*/
Position j;
if (L->Last == MAXSIZE - 1) {
/*表空间已满，不能插入*/
cout<<"表满"<L->Last + 2) {
/*检查插入位序的合法性：是否在1~n+1。n为当前元素个数，即Last+1*/
cout << "位序不合法"<Last; j >= i - 1; j--)/*Last指向序列最后元素*/
L->Data[j + 1] = L->Data[j];/*将位序i及以后的元素顺序向后移动*/
L->Data[i - 1] = X;/*新元素插入第i位序，其数组下标为i-1*/
L->Last++;/*Last仍指向最后元素*/
return true;
} 3）线性表达删除操作
bool LArray::Delete(int i)
{
/*从L中删除指定位序i的元素,该元素数组下标为i-1*/
Position j;
if (i<1 || i>L->Last + 1) {/*检查空表及删除位序的合法性*/
cout << "位序" << i << "不存在元素" << endl;
return false;
}
for (j = i; j <= L->Last; j++)
L->Data[j - 1] = L->Data[j];/*将位序i+1及以后的元素顺序向前移动*/
L->Last--;/*Last仍指向最后元素*/
return true;
}